Similar presentations:
Модели и моделирование. Модели и их типы
1. Модели и моделирование
Тема 1. Модели и их типы2.
Модели в нашей жизни2
3.
Что такое модель?Модель – это объект, который обладает некоторыми
свойствами другого объекта (оригинала) и используется
вместо него.
Оригиналы и модели
Первый линейный русский корабль «Гото Предестинация»
3
4.
Что можно моделировать?Модели объектов:
• уменьшенные копии зданий, кораблей, самолетов, …
• модели ядра атома, кристаллических решеток
• чертежи
•…
Модели процессов:
• изменение экологической обстановки
• экономические модели
• исторические модели
•…
Модели явлений:
• землетрясение
• солнечное затмение
• цунами
•…
4
5.
МоделированиеМоделирование – это создание и использование моделей для
изучения оригиналов.
Когда используют моделирование:
• оригинал не существует
- древний Египет
- последствия ядерной войны (Н.Н. Моисеев, 1966)
• исследование оригинала опасно для жизни или дорого:
- управление ядерным реактором (Чернобыль, 1986)
- испытание нового скафандра для космонавтов
- разработка нового самолета или корабля
• оригинал сложно исследовать непосредственно:
-
Солнечная система, галактика (большие размеры)
атом, нейтрон (маленькие размеры)
процессы в двигателе внутреннего сгорания (очень быстрые)
геологические явления (очень медленные)
• интересуют только некоторые свойства оригинала
- проверка краски для фюзеляжа самолета
5
6.
Цели моделирования• исследование оригинала
изучение сущности объекта или явления
«Наука есть удовлетворение собственного
любопытства за казенный счет» (Л.А. Арцимович)
• анализ («что будет, если …»)
научиться прогнозировать последствия различных
воздействиях на оригинал
• синтез («как сделать, чтобы …»)
научиться управлять оригиналом, оказывая на него
воздействия
• оптимизация («как сделать лучше»)
выбор наилучшего решения в заданных условиях
6
7.
Один оригинал – одна модель?• материальная точка
!
Оригиналу может соответствовать
несколько разных моделей и наоборот!
7
8.
8Зачем нужно много моделей?
!
Тип модели определяется целями моделирования!
изучение
наследственности
изучение
строения
тела
примерка
одежды
учет граждан
страны
тренировка
спасателей
9.
Природа моделей• материальные (физические, предметные) модели:
• информационные модели представляют собой
информацию о свойствах и состоянии объекта,
процесса, явления, и его взаимосвязи с внешним миром:
• вербальные – словесные или мысленные
• знаковые – выраженные с помощью формального языка
графические (рисунки, схемы, карты, …)
табличные
математические (формулы)
логические (различные варианты выбора действий на
основе анализа условий)
специальные (ноты, химические формулы)
9
10.
Модели по области применения• учебные (в т.ч. тренажеры)
• опытные – при создании новых технических средств
аэродинамическая труба
испытания в опытовом бассейне
• научно-технические
имитатор солнечного
излучения
вакуумная камера в Институте
космических исследований
вибростенд
НПО «Энергия»
10
11.
Модели по фактору времени• статические – описывают оригинал в заданный
момент времени
силы, действующие на тело в состоянии покоя
результаты осмотра врача
фотография
• динамические
модель движения тела
явления природы (молния, землетрясение, цунами)
история болезни
видеозапись события
11
12.
Модели по характеру связей• детерминированные
• связи между входными и выходными величинами жестко
заданы
• при одинаковых входных данных каждый раз получаются
одинаковые результаты
Примеры
движение тела без учета ветра
расчеты по известным формулам
• вероятностные (стохастические)
• учитывают случайность событий в реальном мире
• при одинаковых входных данных каждый раз получаются
немного разные результаты
Примеры
движение тела с учетом ветра
броуновское движение частиц
модель движения судна на волнении
модели поведения человека
12
13.
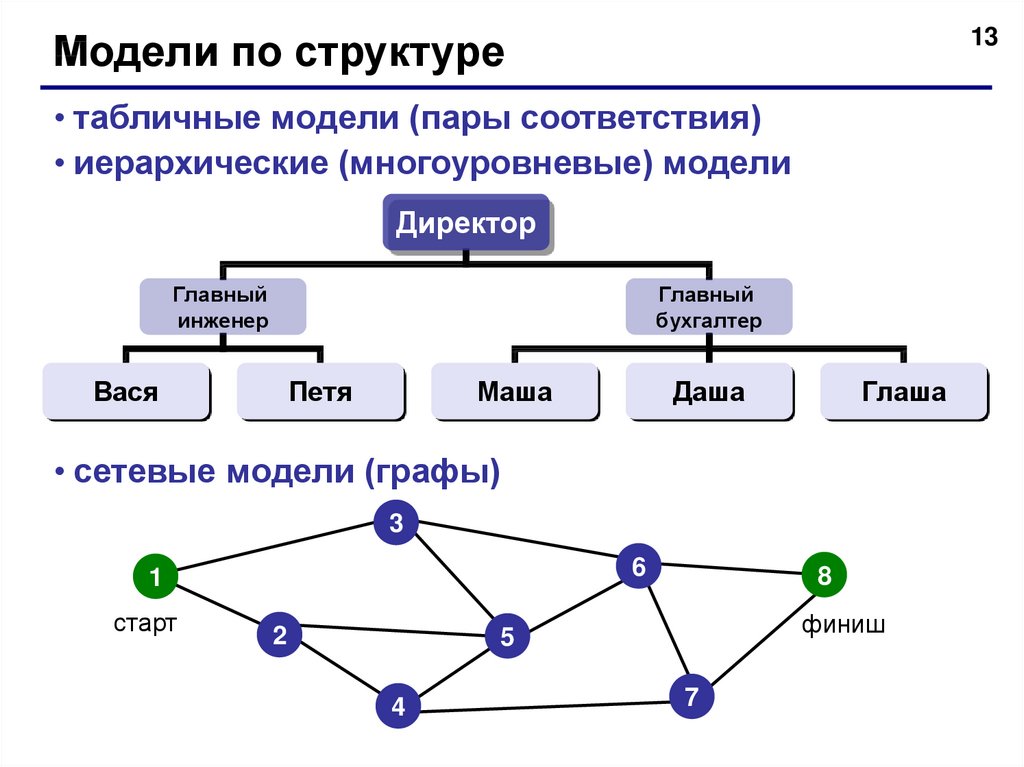
13Модели по структуре
• табличные модели (пары соответствия)
• иерархические (многоуровневые) модели
Директор
Главный
инженер
Главный
бухгалтер
Вася
Петя
Маша
Даша
Глаша
• сетевые модели (графы)
3
6
1
старт
2
8
финиш
5
4
7
14.
Специальные виды моделей• имитационные
- нельзя заранее вычислить или предсказать
поведение системы, но можно имитировать её
реакцию на внешние воздействия;
- максимальный учет всех факторов;
- только численные результаты;
!
Задача – найти лучшее решение методом
проб и ошибок (многократные эксперименты)!
Примеры:
испытания лекарств на мышах, обезьянах, …
математическое моделирование биологических
систем
модели бизнеса и управления
модели процесса обучения
14
15.
Специальные виды моделей• игровые – учитывающие действия противника
Примеры:
модели экономических ситуаций
модели военных действий
спортивные игры
тренинги персонала
!
Задача – найти лучший вариант действий в
самом худшем случае!
15
16.
Адекватность моделиАдекватность – совпадение существенных свойств
модели и оригинала:
результаты моделирования согласуются с
выводами теории (законы сохранения и т.п.)
… подтверждаются экспериментом
!
Адекватность модели можно доказать только
экспериментом!
Модель всегда отличается от оригинала
!
Любая модель адекватна только при
определенных условиях!
16
17.
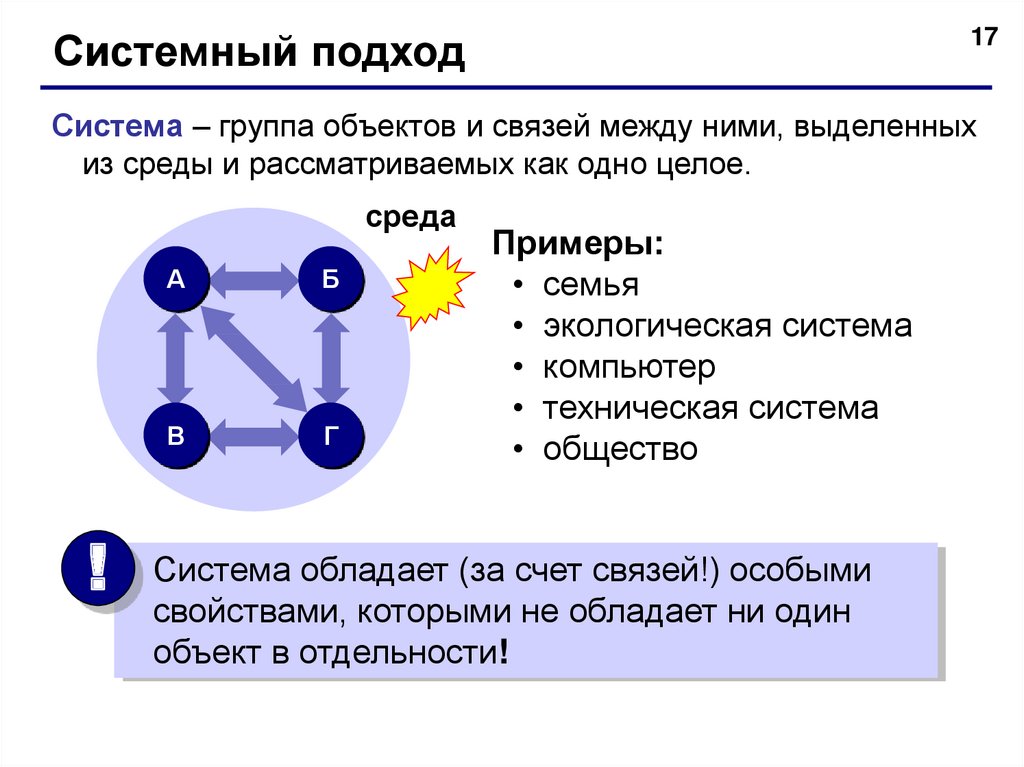
17Системный подход
Система – группа объектов и связей между ними, выделенных
из среды и рассматриваемых как одно целое.
среда
!
А
Б
В
Г
Примеры:
• семья
• экологическая система
• компьютер
• техническая система
• общество
Система обладает (за счет связей!) особыми
свойствами, которыми не обладает ни один
объект в отдельности!
18.
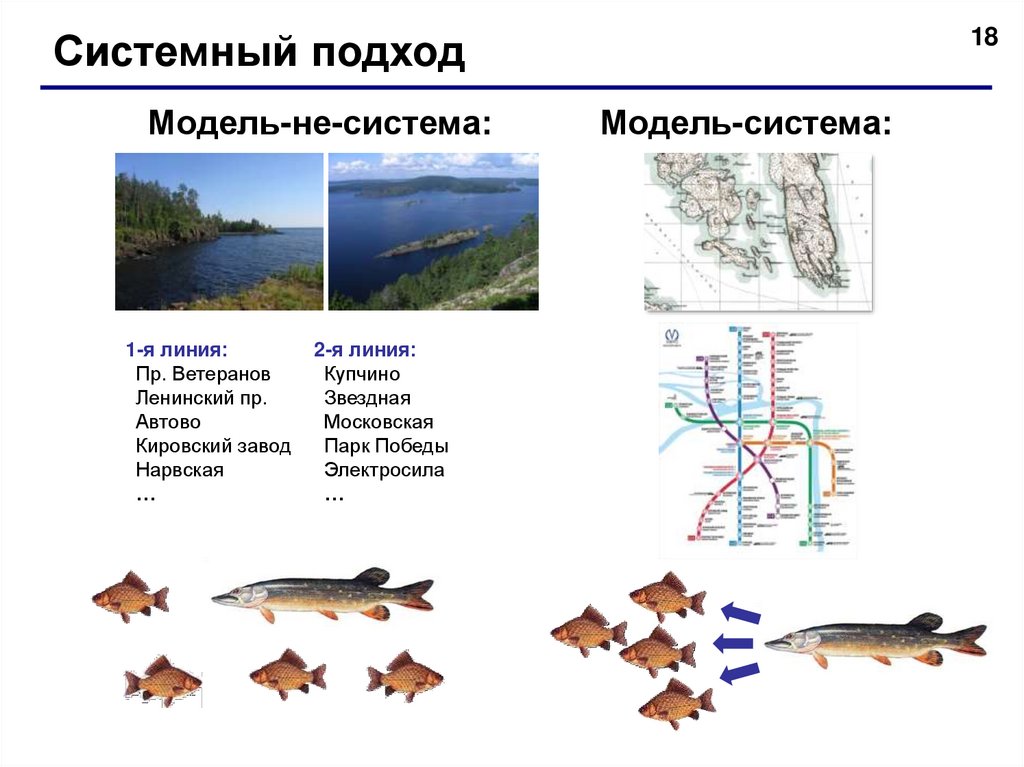
18Системный подход
Модель-не-система:
1-я линия:
Пр. Ветеранов
Ленинский пр.
Автово
Кировский завод
Нарвская
…
2-я линия:
Купчино
Звездная
Московская
Парк Победы
Электросила
…
Модель-система:
19.
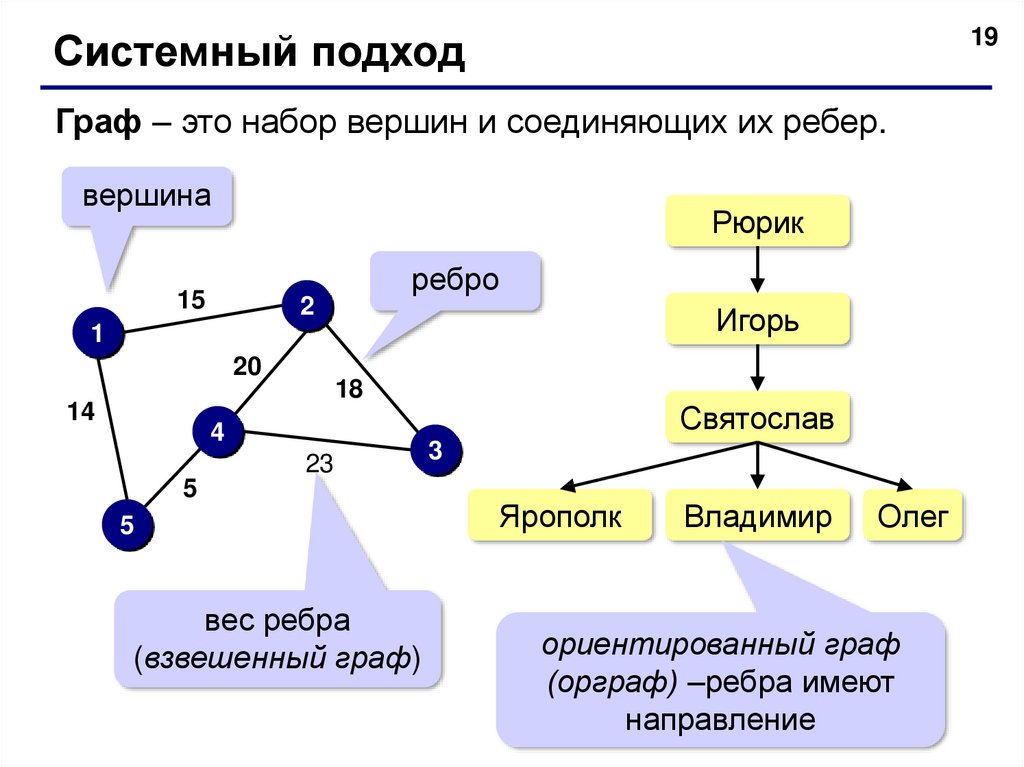
19Системный подход
Граф – это набор вершин и соединяющих их ребер.
вершина
Рюрик
ребро
15
2
Игорь
1
20
14
18
4
23
5
5
вес ребра
(взвешенный граф)
Святослав
3
Ярополк
Владимир
Олег
ориентированный граф
(орграф) –ребра имеют
направление
20.
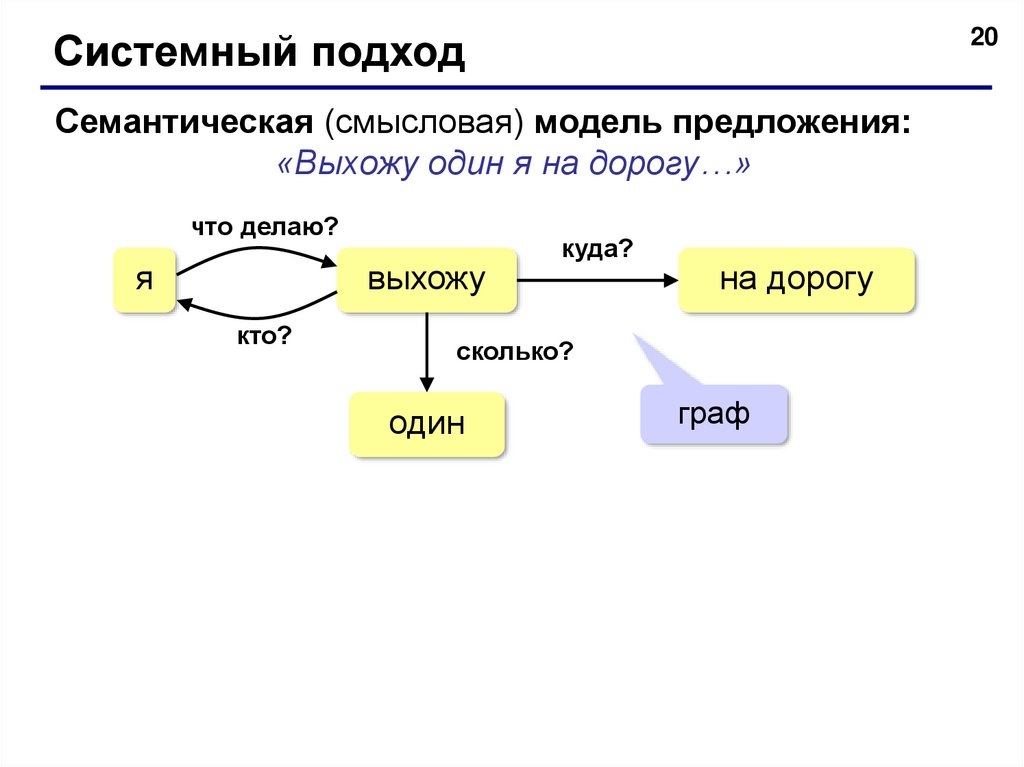
20Системный подход
Семантическая (смысловая) модель предложения:
«Выхожу один я на дорогу…»
что делаю?
я
выхожу
кто?
куда?
на дорогу
сколько?
один
граф
21.
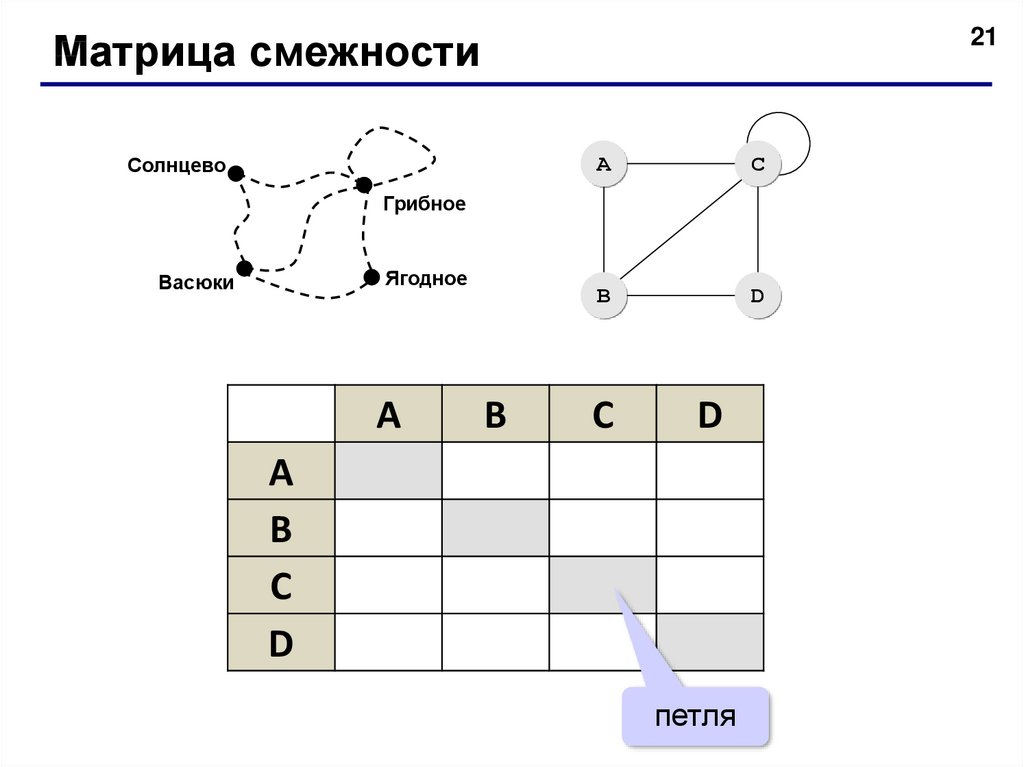
21Матрица смежности
Солнцево
A
C
B
D
Грибное
Ягодное
Васюки
A
B
C
D
A
0
1
1
0
B
1
0
1
1
C
1
1
1
1
D
0
1
1
0
петля
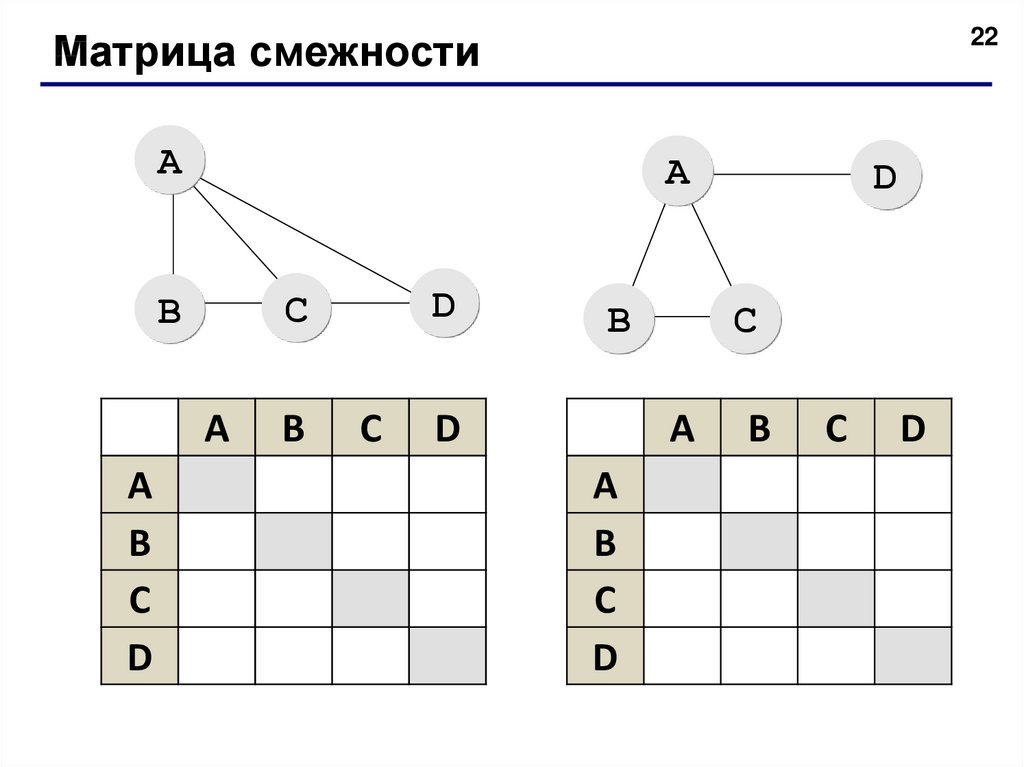
22.
22Матрица смежности
A
A
A
A
B
C
D
D
C
B
B
C
B
D
C
A
A
B
C
D
D
B
C
D
23.
23Матрица смежности
A
A
B
C
D
0
1
1
B
0
1
0
C
1
1
0
D
1
0
0
A
A
B
C
D
1
0
1
B
1
1
0
C
0
1
1
D
1
0
1
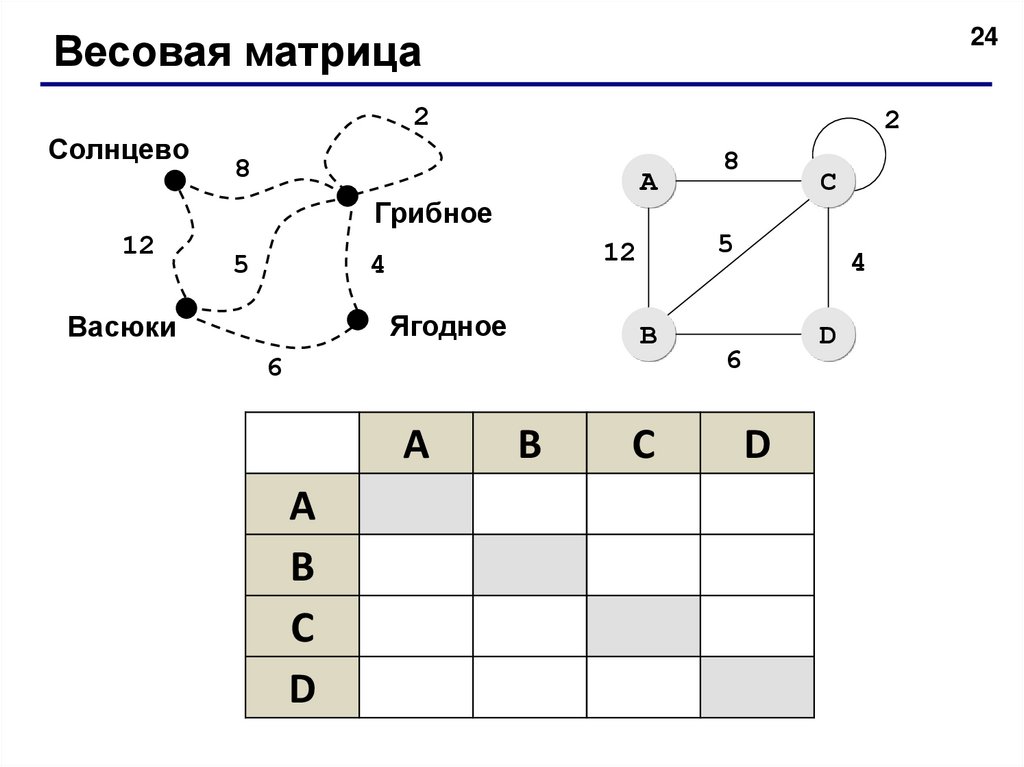
24.
24Весовая матрица
2
Солнцево
2
8
A
Грибное
12
5
Ягодное
Васюки
B
6
A
A
B
C
D
12
8
B
12
5
6
C
5
12
4
8
C
8
5
2
4
4
D
6
D
6
4
25.
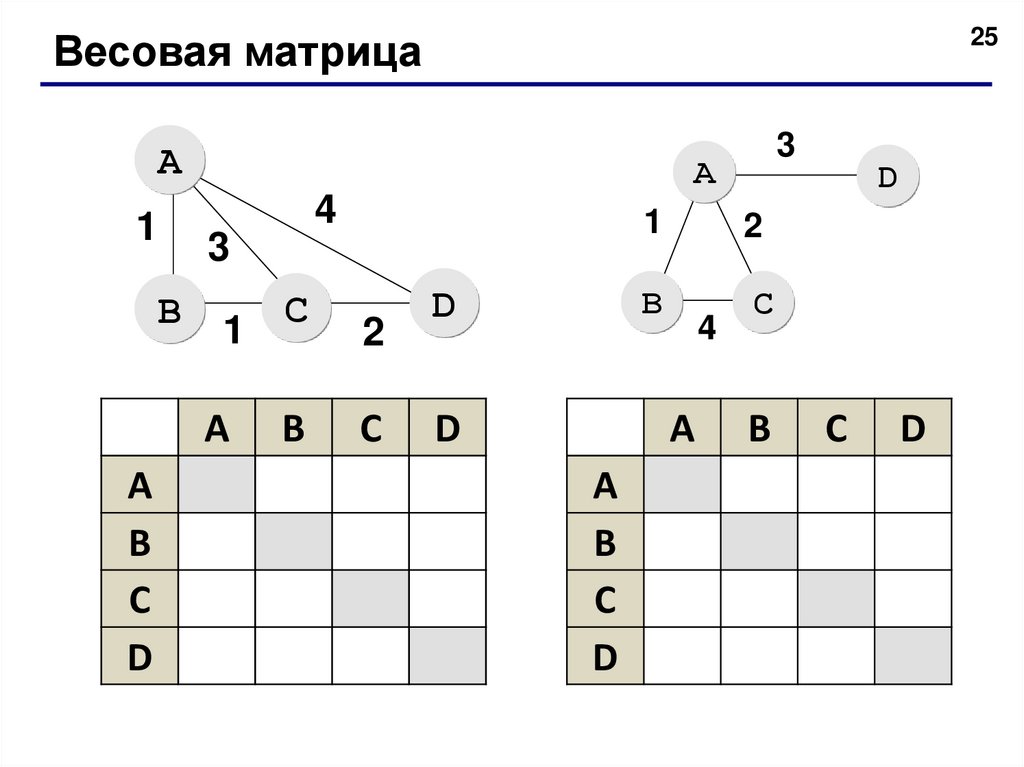
25Весовая матрица
A
A
4
1
3
B
1
A
A
B
C
D
3
C
B
2
C
D
D
1
2
B
C
4
A
A
B
C
D
B
D
C
D
26.
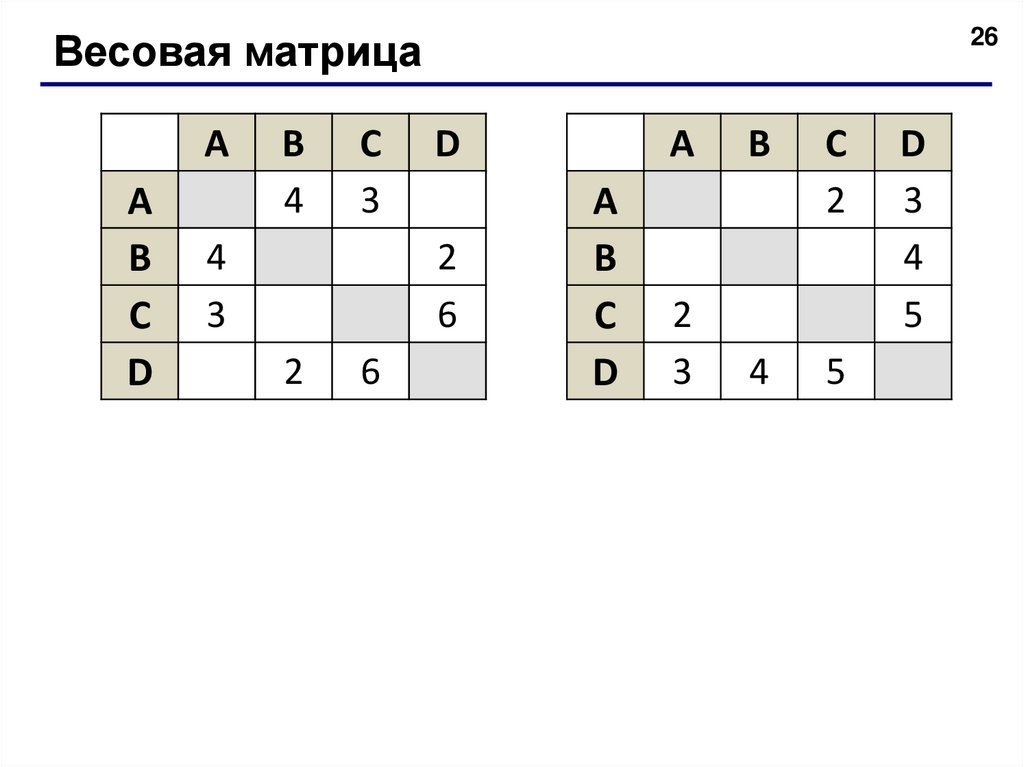
26Весовая матрица
A
A
B
C
D
B
4
C
3
4
3
D
2
6
2
6
A
B
C
D
A
B
C
2
2
3
4
5
D
3
4
5
27.
27Кратчайшие пути
A B
2
A
B 2
C 4 1
D
E 6
C D E
4
6
1
5 1
5
3
1 3
Определите кратчайший путь
между пунктами A и D.
A
2
B
4
С
2
6
E
4
1
С
5
D
8
1
С
3
1
E
4
3
дерево возможных
маршрутов
D
7
6
3
7
D
9
28.
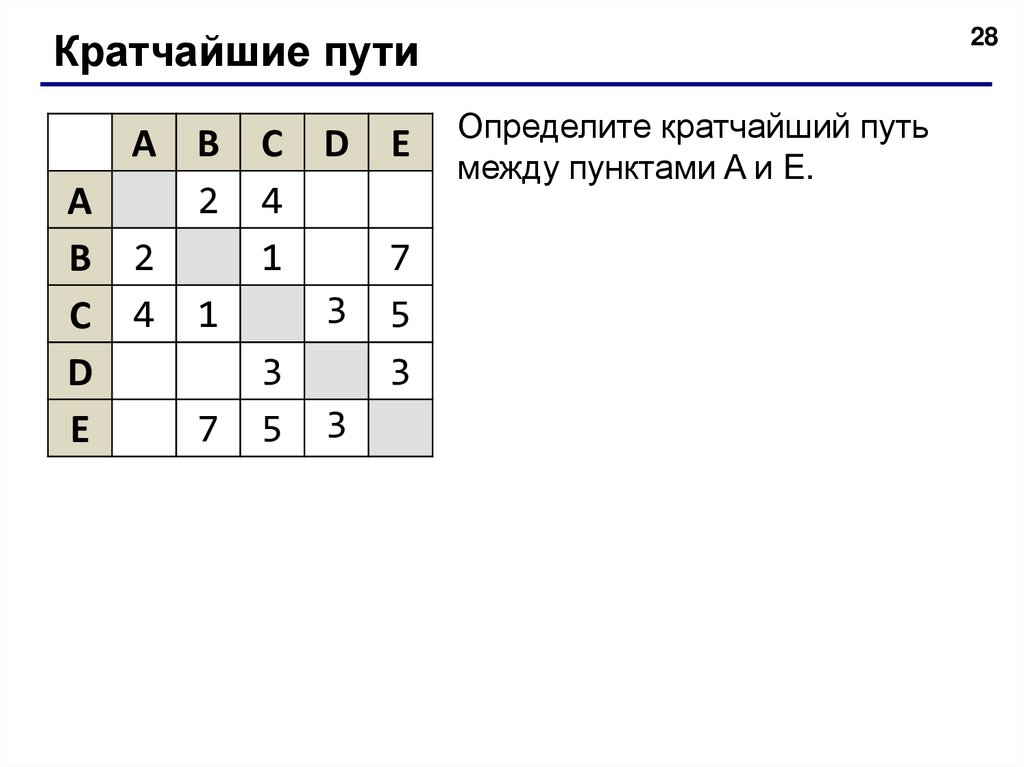
28Кратчайшие пути
A B
2
A
B 2
C 4 1
D
7
E
C D E
4
1
7
3 5
3
3
5 3
Определите кратчайший путь
между пунктами A и E.
29.
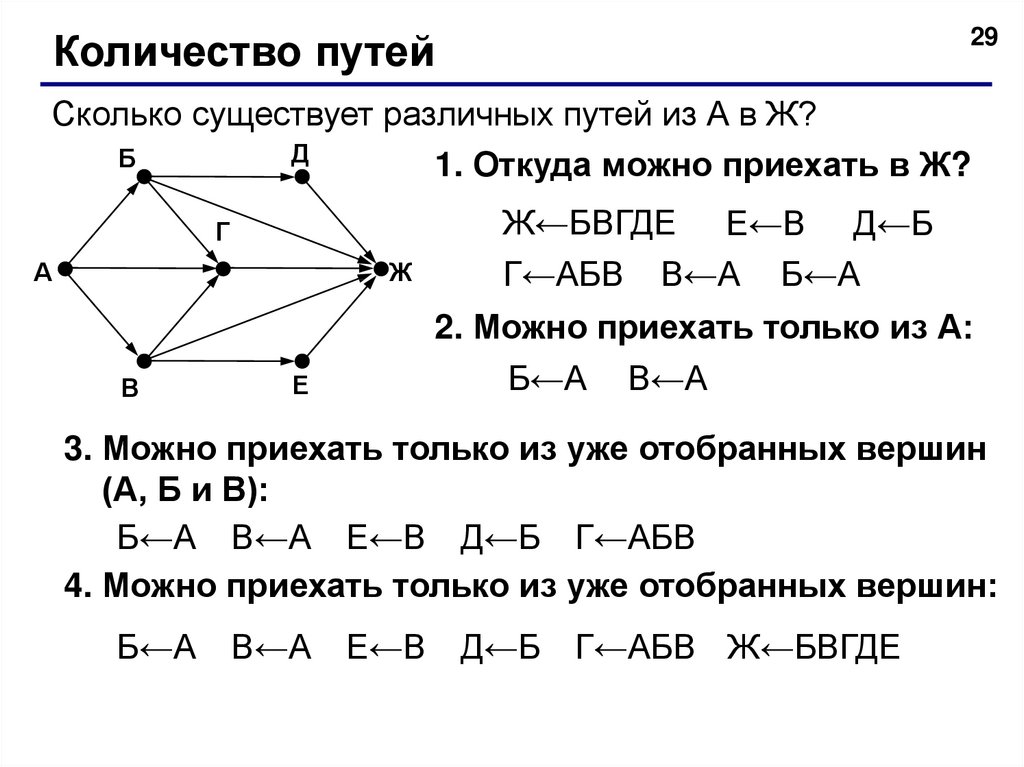
29Количество путей
Сколько существует различных путей из А в Ж?
Д
Б
1. Откуда можно приехать в Ж?
Г
А
Ж
В
Ж←БВГДЕ Е←В Д←Б
Г←АБВ В←А Б←А
2. Можно приехать только из А:
Б←А В←А
Е
3. Можно приехать только из уже отобранных вершин
(А, Б и В):
Б←А В←А Е←В Д←Б Г←АБВ
4. Можно приехать только из уже отобранных вершин:
Б←А
В←А
Е←В
Д←Б
Г←АБВ Ж←БВГДЕ
30.
30Количество путей
После сортировки:
Б←А
!
В←А Е←В Д←Б Г←АБВ
Ж←БВГДЕ
Количество путей в вершину X равно суммарному
количеству путей в каждую из вершин, из которых
есть ребро в X.
Ж←БВГДЕ
NЖ← NБ + NВ + NГ + NД + NЕ
Заполнение таблицы:
Б←А
1
В←А Е←В Д←Б Г←АБВ
1
1
1
3
Ж←БВГДЕ
7
31.
31Количество путей
Форма записи:
Ж←БВГДЕ
Е←В
Д←Б
Г←АБВ
В←А
Б←А
7
1
1
3
1
1
32.
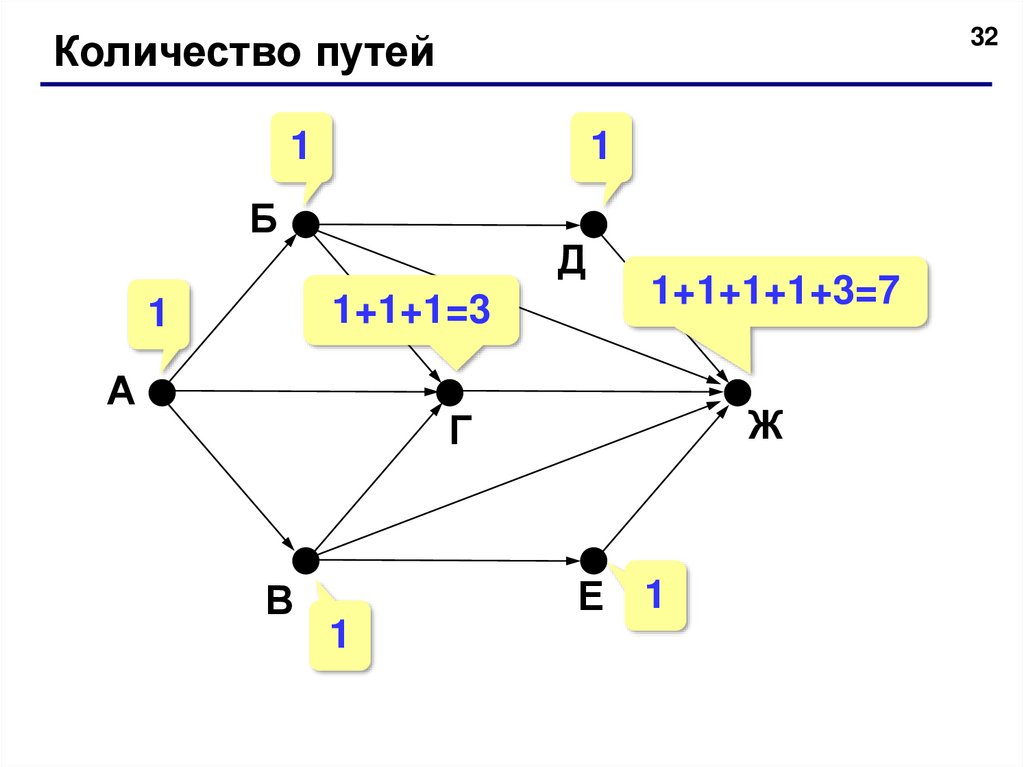
32Количество путей
1
1
Б
Д
1+1+1=3
1
А
1+1+1+1+3=7
Ж
Г
В
Е
1
1
33.
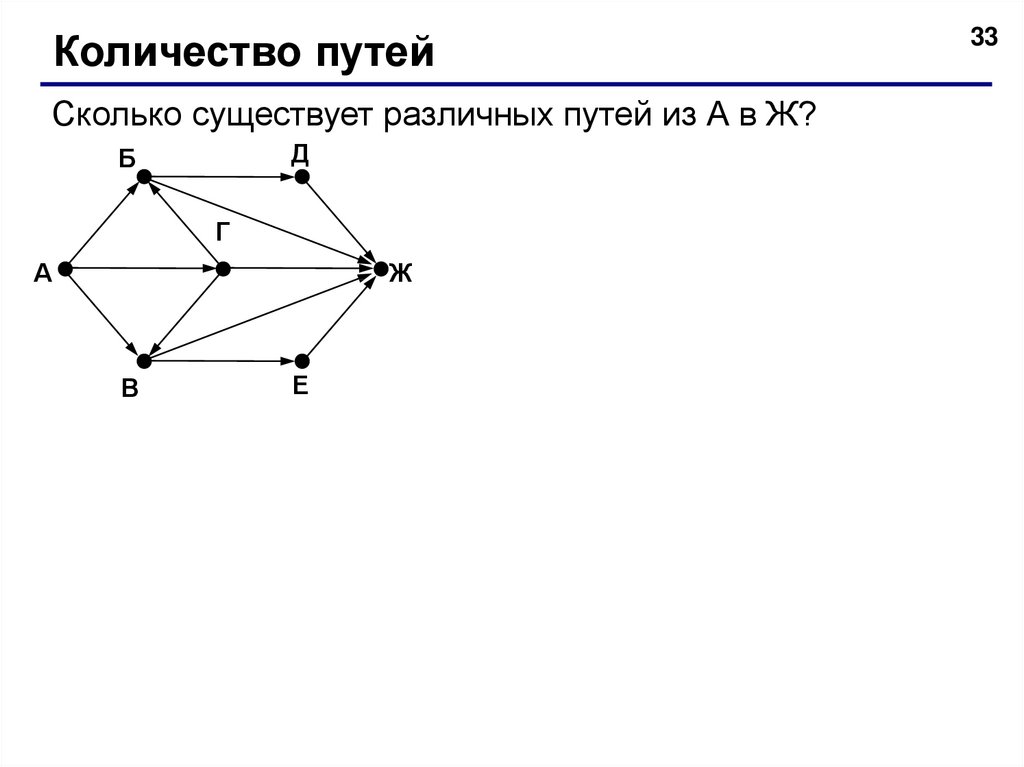
Количество путейСколько существует различных путей из А в Ж?
Д
Б
Г
А
Ж
В
Е
33
34.
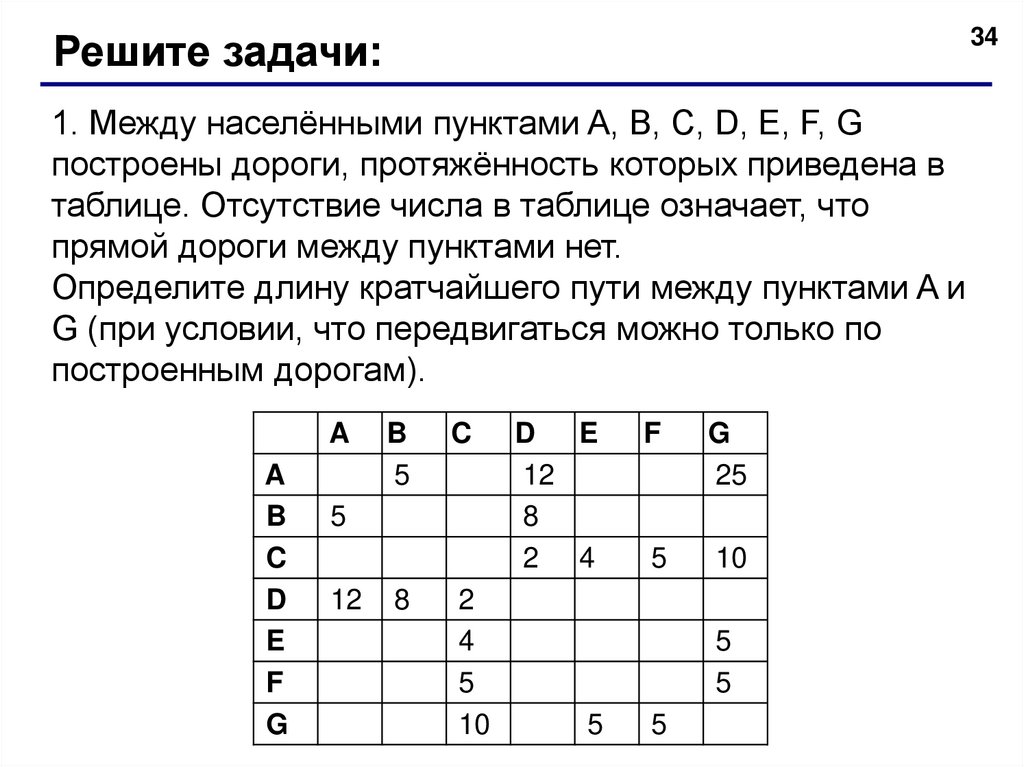
34Решите задачи:
1. Между населёнными пунктами A, B, C, D, E, F, G
построены дороги, протяжённость которых приведена в
таблице. Отсутствие числа в таблице означает, что
прямой дороги между пунктами нет.
Определите длину кратчайшего пути между пунктами A и
G (при условии, что передвигаться можно только по
построенным дорогам).
A
A
B
C
D
E
F
G
B
5
C
5
12
8
2
4
5
10
D
E
12
8
2 4
F
G
25
5
10
5
5
5
5
35.
35Решите задачи:
2. В таблицах приведена протяженность автомагистралей между соседними населенными пунктами. Если пересечение строки и столбца пусто, то соответствующие населенные пункты не соединены автомагистралями. Укажите номер таблицы, для которой выполняется условие
«Максимальная протяженность маршрута от пункта А до
пункта С не больше 5». Протяженность маршрута складывается из протяженности автомагистралей между соответствующими соседними населенными пунктами. При
этом любой населенный пункт должен встречаться на
маршруте не более одного раза.
1.
2.
3.
4.
36.
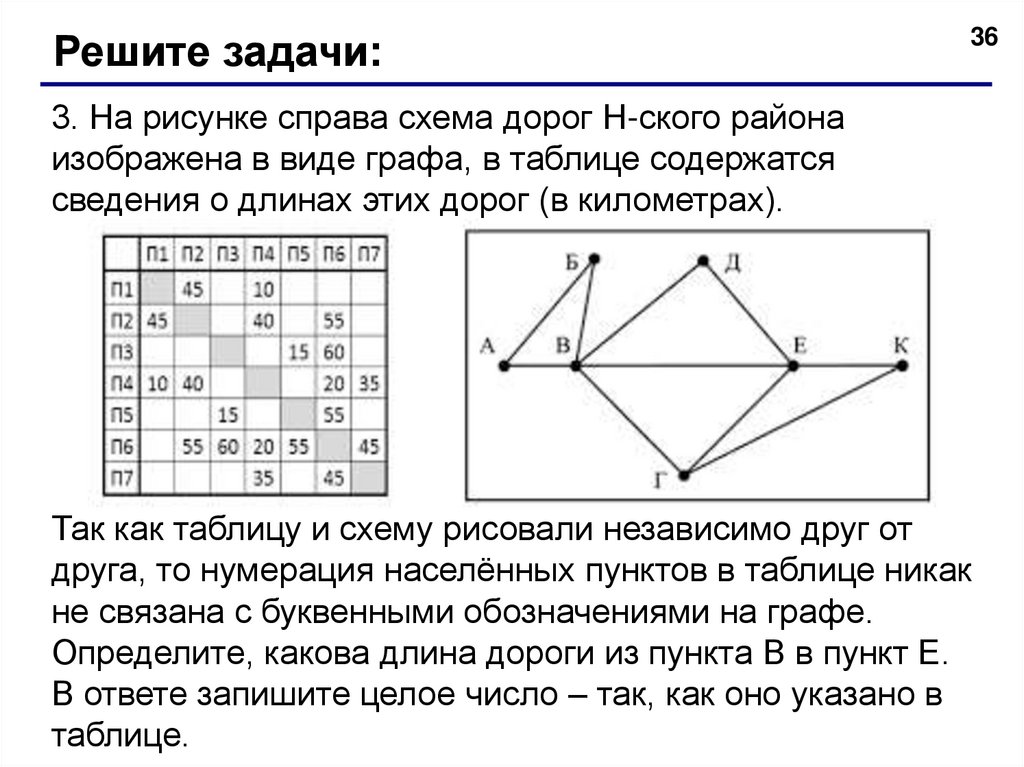
Решите задачи:36
3. На рисунке справа схема дорог Н-ского района
изображена в виде графа, в таблице содержатся
сведения о длинах этих дорог (в километрах).
Так как таблицу и схему рисовали независимо друг от
друга, то нумерация населённых пунктов в таблице никак
не связана с буквенными обозначениями на графе.
Определите, какова длина дороги из пункта В в пункт Е.
В ответе запишите целое число – так, как оно указано в
таблице.
37.
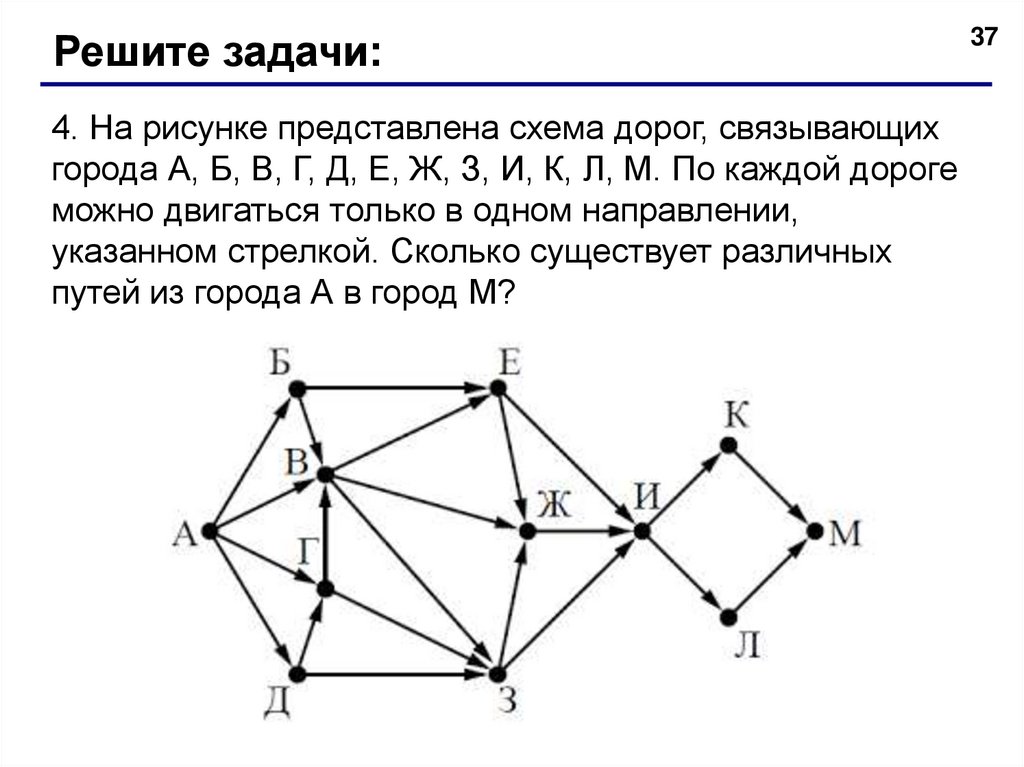
Решите задачи:4. На рисунке представлена схема дорог, связывающих
города А, Б, В, Г, Д, Е, Ж, З, И, К, Л, М. По каждой дороге
можно двигаться только в одном направлении,
указанном стрелкой. Сколько существует различных
путей из города А в город М?
37
38.
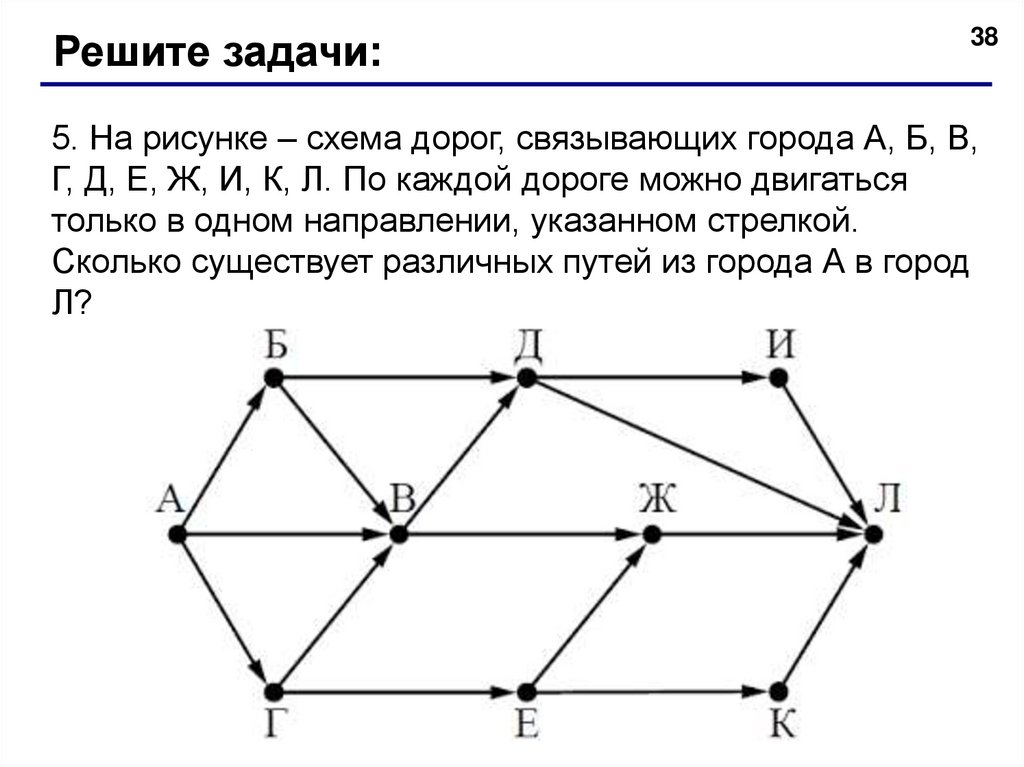
Решите задачи:38
5. На рисунке – схема дорог, связывающих города А, Б, В,
Г, Д, Е, Ж, И, К, Л. По каждой дороге можно двигаться
только в одном направлении, указанном стрелкой.
Сколько существует различных путей из города А в город
Л?
39.
Решите задачи:6. На карту нанесены 4 города (A, B, C и D). Известно,
что
между городами A и С – три дороги
между городами C и B – две дороги
между городами A и B – две дороги
между городами C и D – две дороги
между городами B и D – четыре дороги
По каждой из этих дорог можно ехать в обе стороны.
Сколькими различными способами можно проехать из
города А в город D, посещая каждый город не более
одного раза?
39
40.
Решите задачи:40
7. Исполнитель Май15 преобразует число на экране. У
исполнителя есть две команды, которым присвоены
номера:
1. Прибавить 1
2. Умножить на 2
Первая команда увеличивает число на экране на 1, вторая
умножает его на 2.
Программа для исполнителя Май15 – это
последовательность команд. Сколько существует программ,
для которых при исходном числе 2 результатом является
число 29 и при этом траектория вычислений содержит число
14 и не содержит числа 25? Траектория вычислений
программы – это последовательность
результатов выполнения всех команд программы. Например,
для программы 121 при исходном числе 7 траектория будет
состоять из чисел 8, 16, 17.
41.
Решите задачи:8. У исполнителя Утроитель две команды, которым
присвоены номера:
1. прибавь 1
2. умножь на 3
Первая из них увеличивает число на экране на 1, вторая
– утраивает его.
Программа для Утроителя – это последовательность
команд.
Сколько есть программ, которые число 1 преобразуют в
число 20?
41
42.
Решите задачи:9. У исполнителя Калькулятор две команды, которым
присвоены номера:
1. прибавь 1
2. увеличь две младшие цифры на 1
Первая из них увеличивает число на экране на 1, вторая
– увеличивает на 1 число десятков и число единиц. Если
перед выполнением команды 2 какая-либо из двух
младших цифр равна 9, она не изменяется. Программа
для Калькулятора – это последовательность команд.
Сколько есть программ, которые число 23 преобразуют в
число 48?
42
43.
Решите задачи:43
10. У исполнителя Калькулятор две команды, которым
присвоены номера:
1. прибавь 1
2. увеличь каждый разряд числа на 1
Например, число 23 с помощью команды 2 превратится в
34 а 29 в 39 (так как младший разряд нельзя увеличить).
Программа для Калькулятора – это последовательность
команд. Сколько существует программ, которые число 26
преобразуют в число 49?
44.
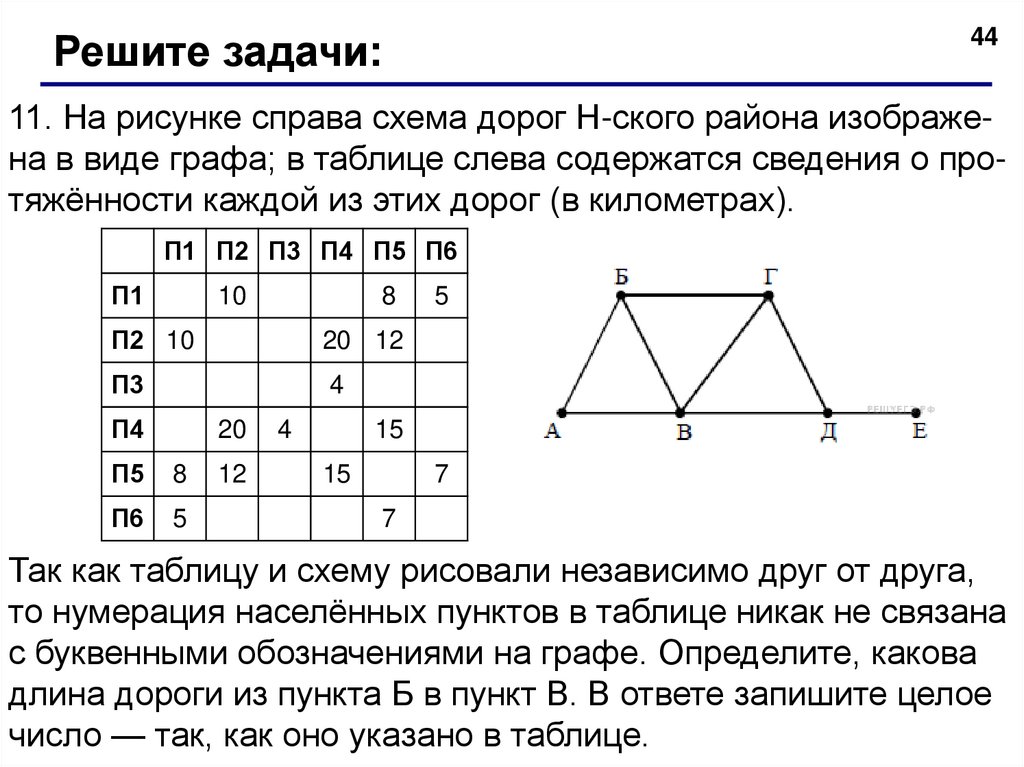
44Решите задачи:
11. На рисунке справа схема дорог Н-ского района изображена в виде графа; в таблице слева содержатся сведения о протяжённости каждой из этих дорог (в километрах).
П1 П2 П3 П4 П5 П6
П1
10
8
П2 10
20 12
П3
4
П4
20
П5
8
П6
5
12
4
5
15
15
7
7
Так как таблицу и схему рисовали независимо друг от друга,
то нумерация населённых пунктов в таблице никак не связана
с буквенными обозначениями на графе. Определите, какова
длина дороги из пункта Б в пункт В. В ответе запишите целое
число — так, как оно указано в таблице.
45.
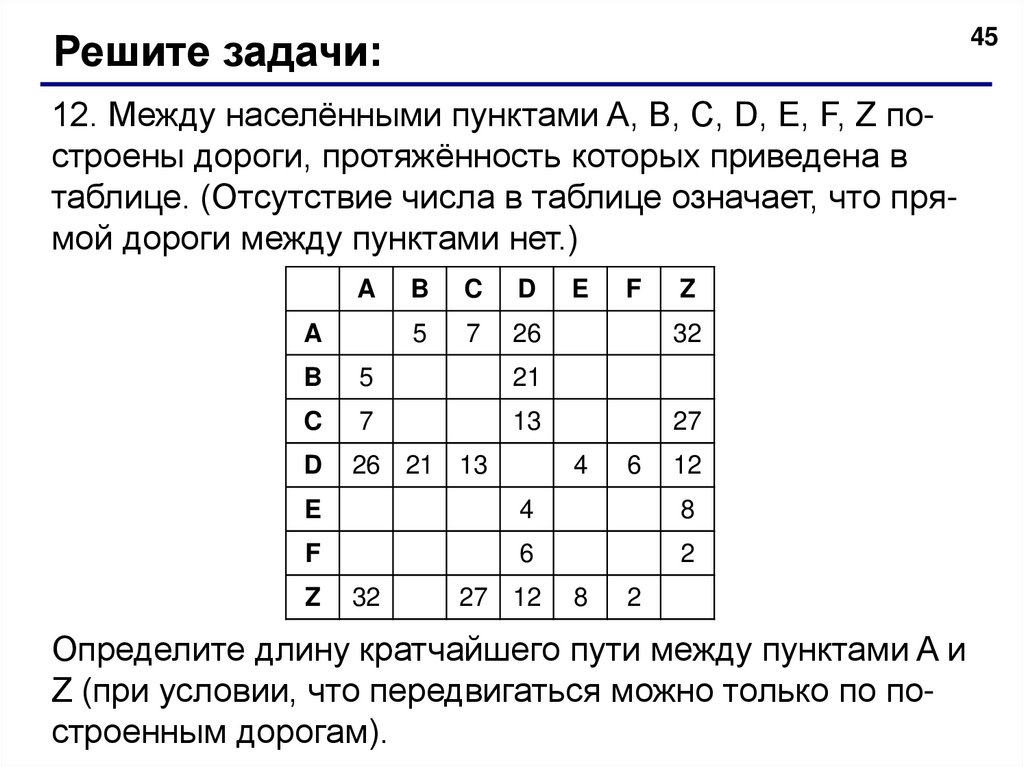
45Решите задачи:
12. Между населёнными пунктами A, B, C, D, E, F, Z построены дороги, протяжённость которых приведена в
таблице. (Отсутствие числа в таблице означает, что прямой дороги между пунктами нет.)
A
A
B
C
D
5
7
26
B
5
21
C
7
13
D
26 21 13
E
F
Z
32
27
4
6
12
E
4
8
F
6
2
Z
32
27 12
8
2
Определите длину кратчайшего пути между пунктами A и
Z (при условии, что передвигаться можно только по построенным дорогам).
46.
46Решите задачи:
13. В таблицах приведена протяженность автомагистралей
между соседними населенными пунктами. Если пересечение строки и столбца пусто, то соответствующие населенные пункты не являются соседними. Укажите номер таблицы, для которой выполняется условие «Максимальная протяженность маршрута от пункта C до пункта B не больше
6». Протяженность маршрута складывается из протяженности автомагистралей между соответствующими соседними
населенными пунктами. При этом через любой населенный
пункт маршрут должен проходить не более одного раза.
1.
2.
3.
4.
47.
Решите задачи:14. Исполнитель Увеличитель234 преобразует число, записанное на экране. У исполнителя три команды, которым присвоены номера:
1. Прибавь 2
2. Прибавь 3
3. Прибавь 4
Первая из них увеличивает число на экране на 2, вторая
увеличивает это число на 3, а третья – на 4. Программа
для исполнителя Увеличитель234 – это последовательность команд.
Сколько есть программ, которые число 23 преобразуют в
число 38?
47
48.
Решите задачи:15. Исполнитель Увеличитель345 преобразует число, записанное на экране. У исполнителя три команды, которым присвоены номера:
1. Прибавь 3
2. Прибавь 4
3. Прибавь 5
Первая из них увеличивает число на экране на 3, вторая
увеличивает это число на 4, а третья – на 5. Программа
для исполнителя Увеличитель345 – это последовательность команд.
Сколько есть программ, которые число 22 преобразуют в
число 42?
48
49.
Ответы к задачам:1. 23
2. 4
3. 20
4. 56
5. 13
6. 46
7. 13
8. 12
9. 26
10. 22
11. 8
12. 28
13. 3
14. 112
15. 73
49
50. Модели и моделирование
Тема 2. Этапы моделирования51.
I. Постановка задачи51
• исследование оригинала
изучение сущности объекта или явления
• анализ («что будет, если …»)
научиться прогнозировать последствий при различных
воздействиях на оригинал
• синтез («как сделать, чтобы …»)
научиться управлять оригиналом, оказывая на него
воздействия
• оптимизация («как сделать лучше»)
выбор наилучшего решения в заданных условиях
!
Ошибки при постановке задачи приводят к
наиболее тяжелым последствиям!
52.
I. Постановка задачи52
Хорошо поставленная задача:
• описаны все связи между исходными данными и
результатом
• известны все исходные данные
• решение существует
• задача имеет единственное решение
Примеры плохо поставленных задач:
• Винни Пух и Пятачок построили ловушку для
слонопотама. Удастся ли его поймать?
• Малыш и Карлсон решили по–братски разделить два
орешка – большой и маленький. Как это сделать?
• Найти максимальное значение функции y = x2 (нет
решений).
• Найти функцию, которая проходит через точки (0,1) и (1,0)
(неединственное решение).
53.
II. Разработка модели• выбрать тип модели
• определить существенные свойства оригинала,
которые нужно включить в модель, отбросить
несущественные (для данной задачи)
• построить формальную модель
это модель, записанная на формальном языке
(математика, логика, …) и отражающая только
существенные свойства оригинала
• разработать алгоритм работы модели
алгоритм – это четко определенный порядок
действий, которые нужно выполнить для решения
задачи
53
54.
III. Тестирование модели54
Тестирование – это проверка модели на простых
исходных данных с известным результатом.
Примеры:
• устройство для сложения многозначных чисел –
проверка на однозначных числах
• модель движения корабля – если руль стоит ровно,
курс не должен меняться; если руль повернуть влево,
корабль должен идти вправо
• модель накопления денег в банке – при ставке 0%
сумма не должна изменяться
?
Модель прошла тестирование. Гарантирует
ли это ее правильность?
55.
IV. Эксперимент c модельюЭксперимент – это исследование модели в
интересующих нас условиях.
Примеры:
• устройство для сложения чисел – работа с
многозначными числами
• модель движения корабля – исследование в
условиях морского волнения
• модель накопления денег в банке – расчеты
при ненулевой ставке
?
Можно ли 100%-но верить результатам?
55
56.
V. Проверка практикой, анализ результатовВозможные выводы:
• задача решена, модель адекватна
• необходимо изменить алгоритм или условия
моделирования
• необходимо изменить модель (например,
учесть дополнительные свойства)
• необходимо изменить постановку задачи
56
57.
57Пример.
Задача. Обезьяна хочет
сбить бананы на
пальме. Как ей надо
кинуть кокос, чтобы
попасть им в бананы.
Анализ задачи:
• все ли исходные
данные известны?
• есть ли решение?
• единственно ли
решение?
58.
I. Постановка задачи58
Допущения:
• кокос и банан считаем материальными точками
• расстояние до пальмы известно
• рост обезьяны известен
• высота, на которой висит банан, известна
• обезьяна бросает кокос с известной начальной
скоростью
• сопротивление воздуха не учитываем
При этих условиях требуется найти начальный угол, под
которым надо бросить кокос.
?
Всегда ли есть решение?
59.
59II. Разработка модели
Графическая модель
y
V
H
h
x
L
Формальная (математическая) модель
x V cos t ,
gt 2
y h V sin t
2
Задача: найти t, , при которых
V cos t L,
gt 2
h V sin t
H
2
60.
III. Тестирование моделиМатематическая модель
x V cos t
gt 2
y h V sin t
2
• при нулевой скорости кокос падает вертикально вниз
• при t=0 координаты равны (0,h)
• при броске вертикально вверх ( =90o) координата x не
меняется
• при некотором t координата y начинает уменьшаться
(ветви параболы вниз)
!
Противоречий не обнаружено!
60
61.
61IV. Эксперимент
Метод I.
Меняем угол . Для выбранного угла строим
траекторию полета ореха. Если она проходит выше
банана, уменьшаем угол, если ниже – увеличиваем.
Метод II.
Из первого равенства выражаем время полета:
V cos t L
L
t
V cos
Меняем угол . Для выбранного угла считаем t, а
затем – значение y при этом t. Если оно больше H,
уменьшаем угол, если меньше – увеличиваем.
не надо строить всю траекторию для каждого
62.
V. Анализ результатов1. Всегда ли обезьяна может сбить банан?
2. Что изменится, если обезьяна может бросать кокос с
разной силой (с разной начальной скоростью)?
3. Что изменится, если кокос и бананы не считать
материальными точками?
4. Что изменится, если требуется учесть сопротивление
воздуха?
5. Что изменится, если дерево качается?
62
63. Модели и моделирование
Тема 3. Модели биологических систем(по мотивам учебника А.Г. Гейна и др., Информатика и ИКТ,
10 класс, М.: Просвещение, 2008)
64.
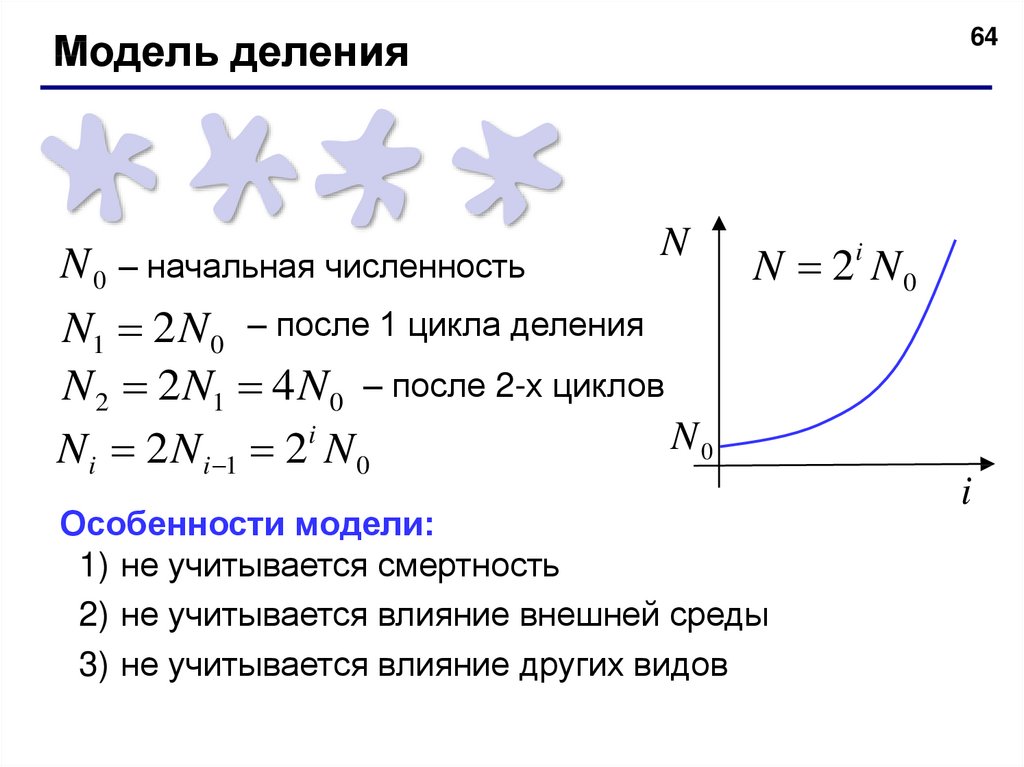
64Модель деления
N
i
N 0 – начальная численность
N 2 N0
N1 2N 0 – после 1 цикла деления
N 2 2 N1 4 N0 – после 2-х циклов
i
N0
N i 2 N i 1 2 N 0
Особенности модели:
1) не учитывается смертность
2) не учитывается влияние внешней среды
3) не учитывается влияние других видов
i
65.
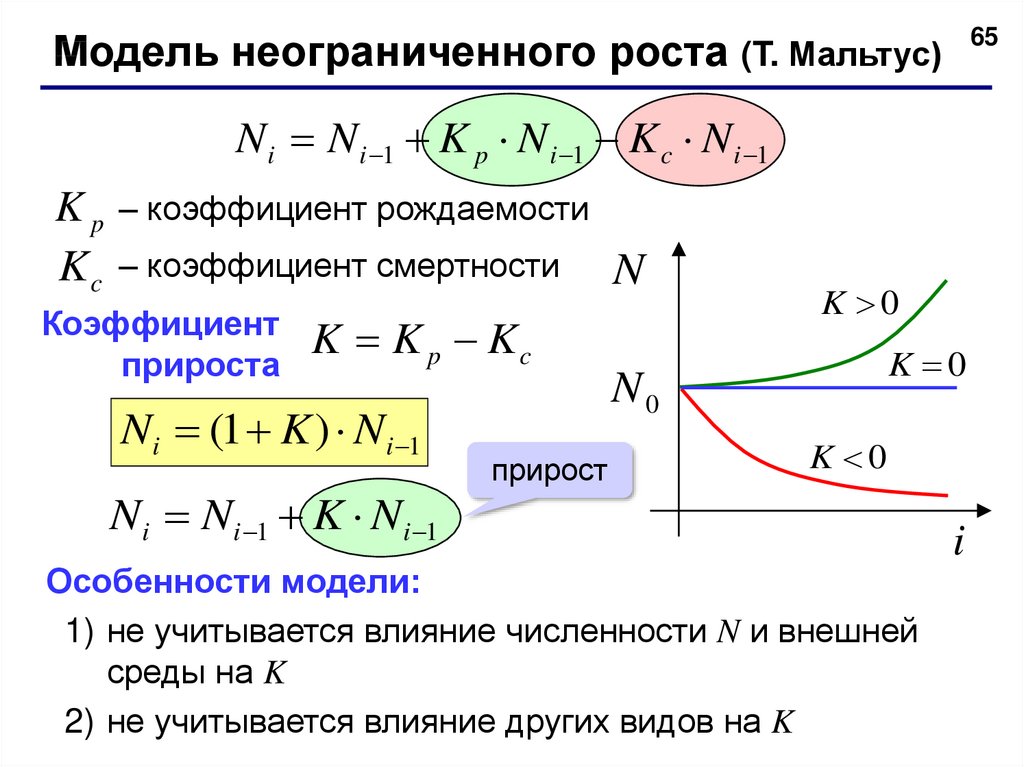
65Модель неограниченного роста (T. Мальтус)
N i N i 1 K p N i 1 K c N i 1
Kp
Kc
– коэффициент рождаемости
– коэффициент смертности
Коэффициент
прироста
N
K K p Kc
Ni (1 K ) Ni 1
Ni Ni 1 K Ni 1
K 0
K 0
N0
прирост
K 0
Особенности модели:
1) не учитывается влияние численности N и внешней
среды на K
2) не учитывается влияние других видов на K
i
66.
Модель ограниченного роста (П. Ферхюльст)L – предельная численность животных
Ni (1 K L ) Ni 1
Идеи:
1) коэффициент прироста KL зависит от численности N
2) при N=0 должно быть KL=K (начальное значение)
3) при N=L должно быть KL=0 (достигнут предел)
L N i 1
N i 1 K
N i 1
L
!
Модель адекватна,
если ошибка < 10%!
N
L
N0
i
66
67.
67Модель с отловом
Примеры: рыбоводческое хозяйство, разведение
пушных зверей и т.п.
L N i 1
N i 1 K
N i 1 R
L
?
отлов
Какая будет численность?
N i N i 1, прирост = отлову
L N
N N K
N R
L
?
K
N2 K N R 0
L
Сколько можно отловить?
68.
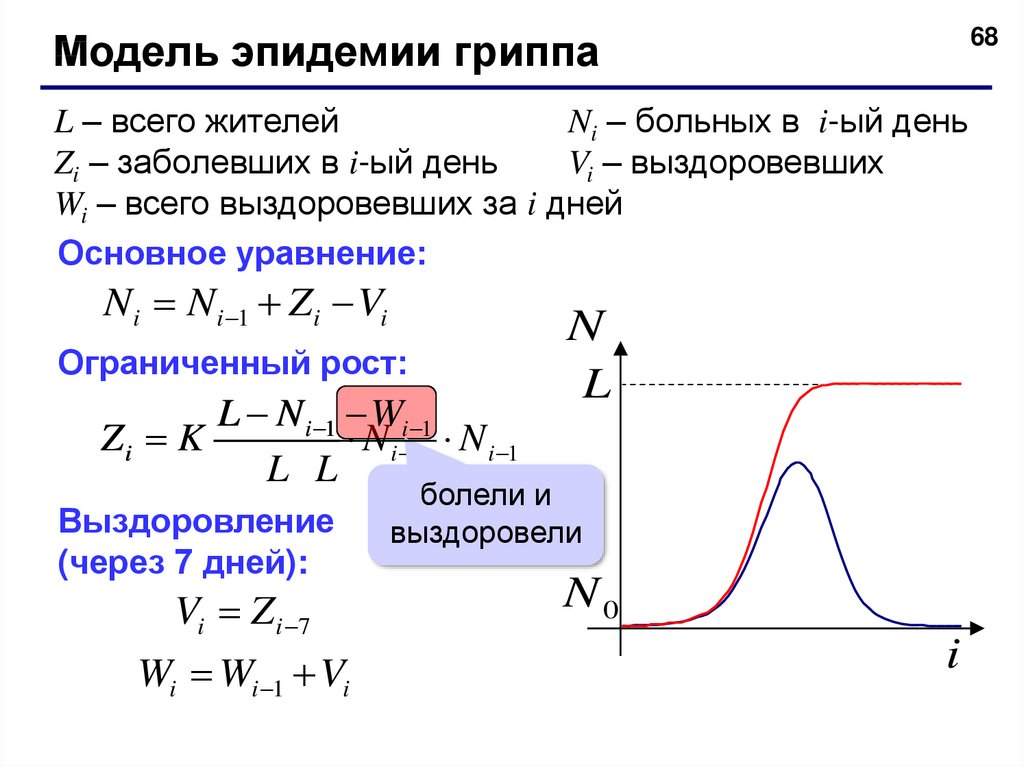
68Модель эпидемии гриппа
L – всего жителей
Ni – больных в i-ый день
Zi – заболевших в i-ый день
Vi – выздоровевших
Wi – всего выздоровевших за i дней
Основное уравнение:
Ni Ni 1 Zi Vi
Ограниченный рост:
L N i 1 Wi 1
Zi K
N i 1 N i 1
L L
Выздоровление
(через 7 дней):
Vi Z i 7
Wi Wi 1 Vi
N
L
болели и
выздоровели
N0
i
69.
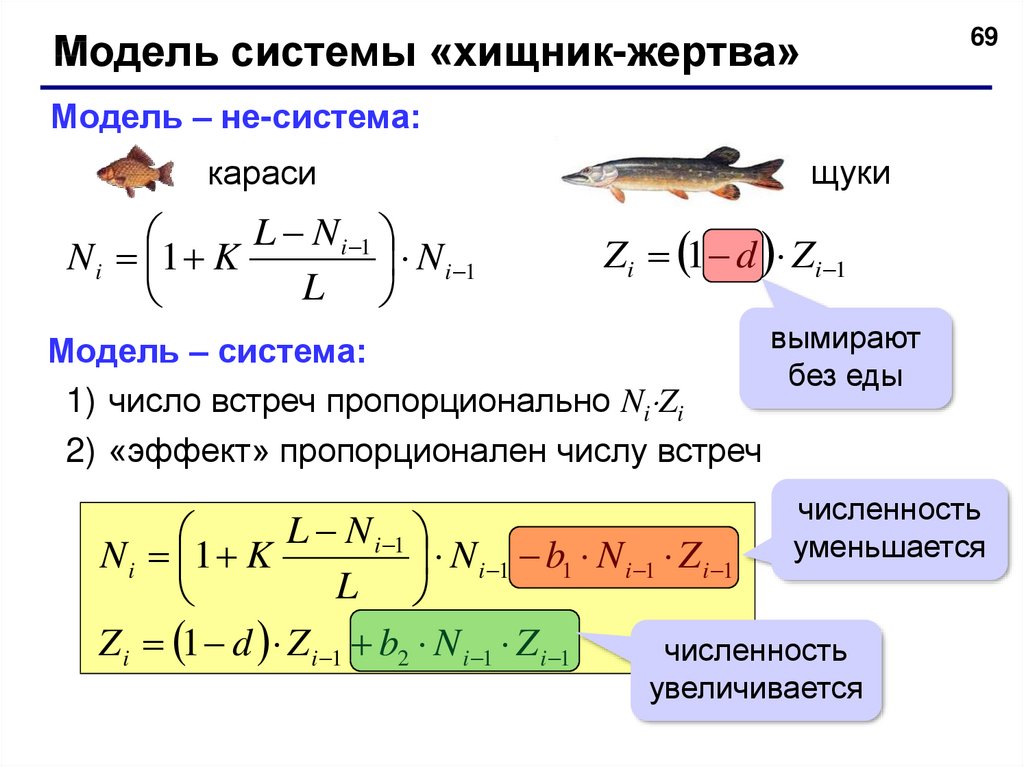
69Модель системы «хищник-жертва»
Модель – не-система:
караси
L N i 1
N i 1 K
N i 1
L
щуки
Zi 1 d Zi 1
вымирают
Модель – система:
без еды
1) число встреч пропорционально Ni Zi
2) «эффект» пропорционален числу встреч
численность
уменьшается
L N i 1
N i 1 K
N i 1 b1 N i 1 Z i 1
L
Z i 1 d Z i 1 b2 N i 1 Z i 1
численность
увеличивается
70.
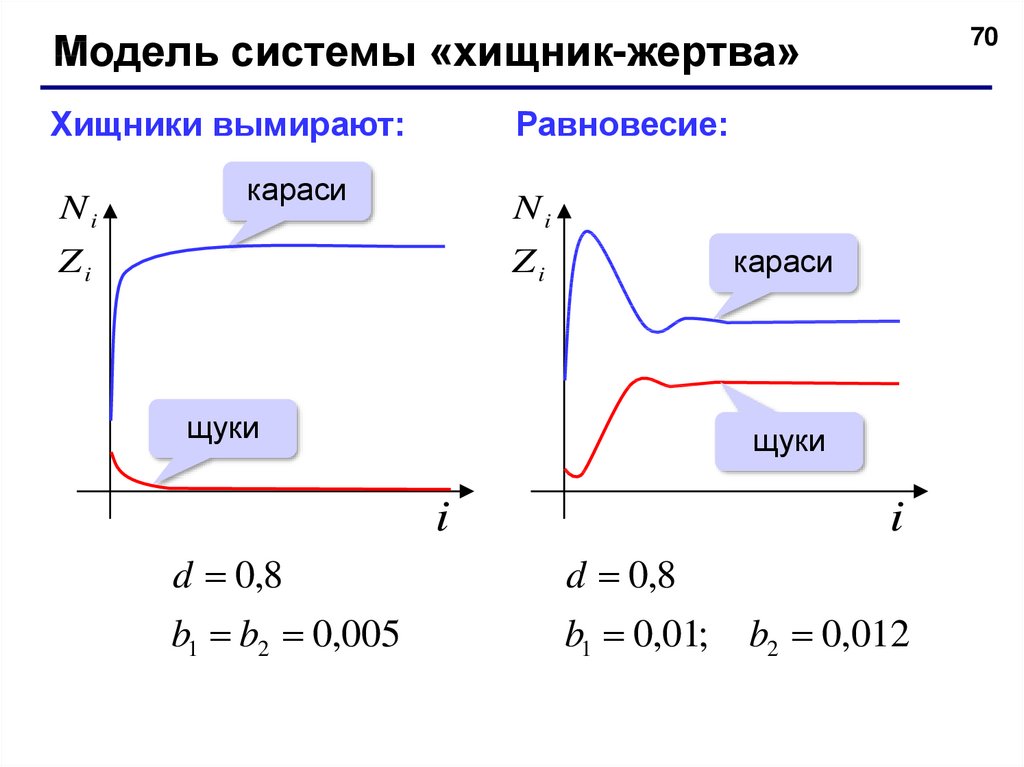
70Модель системы «хищник-жертва»
Хищники вымирают:
Ni
Равновесие:
караси
Ni
Zi
караси
Zi
щуки
щуки
i
d 0,8
b1 b2 0,005
i
d 0,8
b1 0,01;
b2 0,012
71.
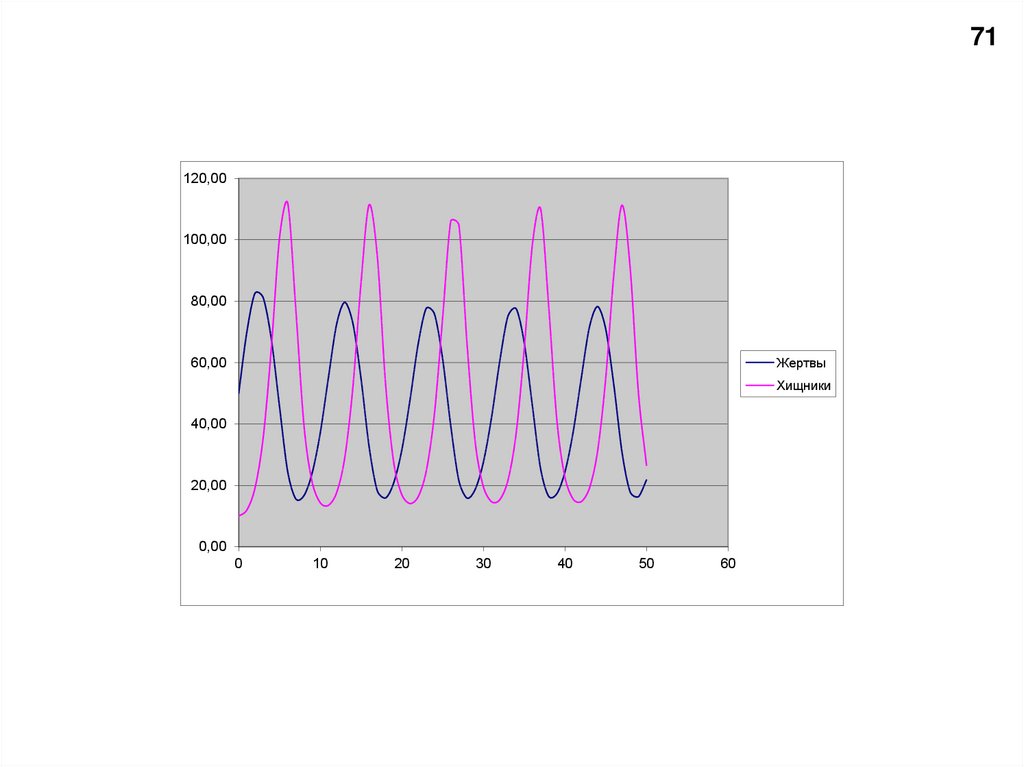
71120,00
100,00
80,00
60,00
Жертвы
Хищники
40,00
20,00
0,00
0
10
20
30
40
50
60
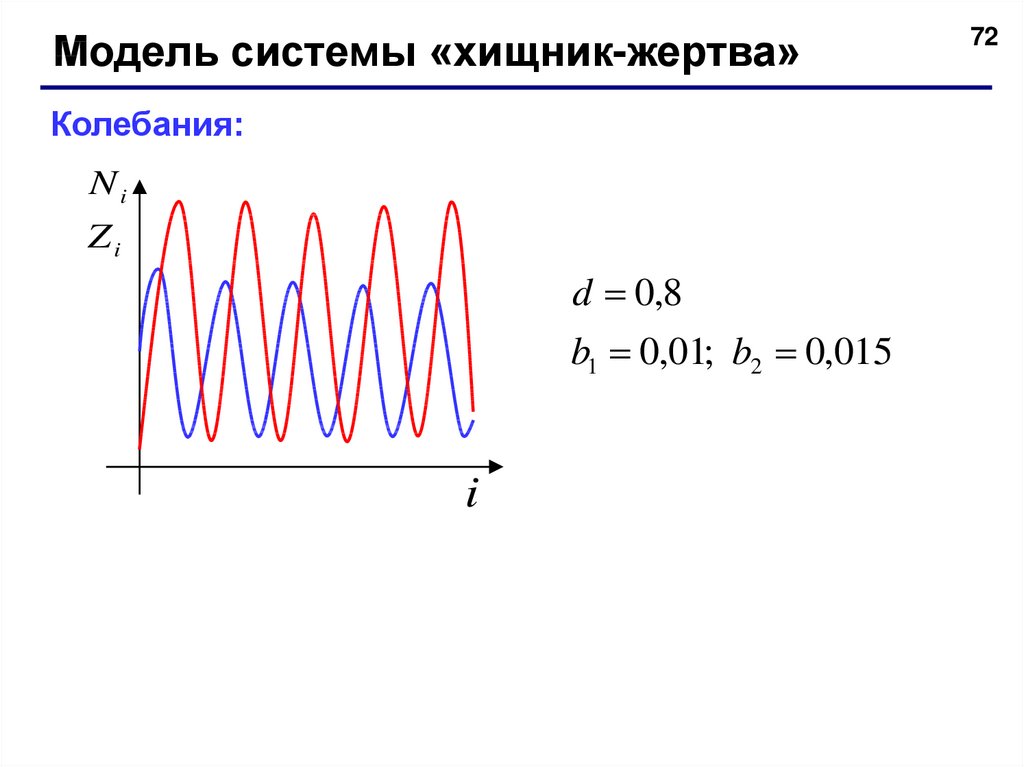
72.
Модель системы «хищник-жертва»Колебания:
Ni
Zi
d 0,8
b1 0,01; b2 0,015
i
72













































 informatics
informatics








