Системы линейных уравнений и способы их решения

1.

Системы линейных
уравнений
и способы их
решения

2.

1. Общий вид, основные понятия, матричная форма
Система m линейных уравнений с n неизвестными имеет вид:
a11 x1 a12 x2 ... a1n xn b1 ,
a x a x ... a x b ,
21 1 22 2
2n n
2
...........................................
am1 x1 am 2 x2 ... amn xn bm
где
aij , bi R
aij коэффициенты при неизвестных,
bi свободные коэффициенты.

3.

Система линейных уравнений (СЛУ)
Совместная
(имеет хотя бы одно решение)
Определённая
(имеет единственное решение)
Несовместная
(не имеет ни одного решения)
Неопределённая
(имеет более одного решениябесконечное множество решений)
В случае неопределённой системы каждое её решение
называется частным решением системы.
Совокупность всех частных решений называется общим
решением.

4.

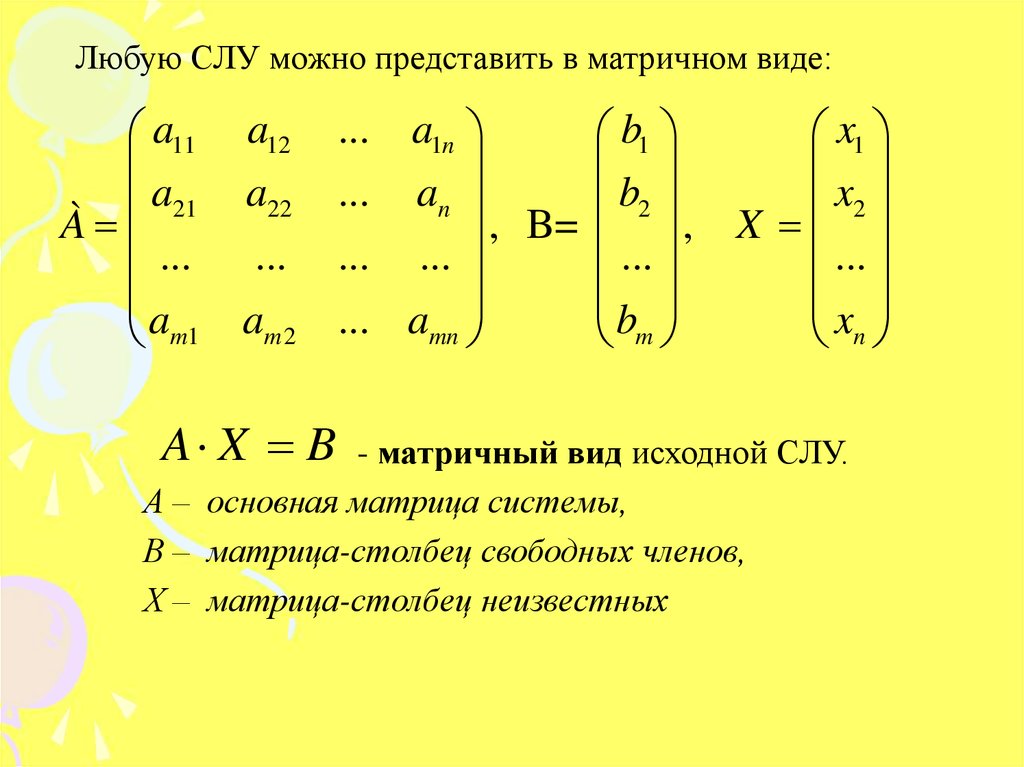
Любую СЛУ можно представить в матричном виде:
a11
a21
À
...
am1
a12
a22
...
am 2
A X B
... a1n
b1
... an
b2
, B=
,
...
... ...
... amn
bm
x1
x2
X
...
xn
- матричный вид исходной СЛУ.
А – основная матрица системы,
В – матрица-столбец свободных членов,
Х – матрица-столбец неизвестных

5.

1) Метод обратной матрицы
Метод основан на нахождении обратной матрицы, поэтому
применим к СЛУ размерности nxn.
Рассмотрим СЛУ в матричном виде:
1
1) AX B X A B
1
2) XA B X BA

6.

2) Метод последовательного исключения неизвестных
(Метод Гаусса)
Рассмотрим СЛУ:
a11 x1 a12 x2 ... a1n xn b1 ,
a x a x ... a x b ,
21 1 22 2
2n n
2
...........................................
am1 x1 am 2 x2 ... amn xn bm
Данный метод применим к СЛУ любой размерности.

7.

1.
Алгоритм метода:
Составим расширенную матрицу.
a11
A* a21
am1
a12
a22
am 2
a1n
a2 n
amn
b1
b2
bm
2. С помощью элементарных преобразований строк
расширенную матрицу приведём к треугольному
(ступенчатому) виду.
a11 a12
a 21 a 22
a
31 a 32
a13
a 23
a 33
b1
b2
b 3
1 c 12
0 1
0 0
c 13
c 23
1
d1
d2
d3
3. Вернувшись к системе уравнений, находим неизвестные.

8.

Элементарными преобразованиями матрицы
называют:
• Умножение какой-нибудь строки (столбца) на
отличное от нуля число.
• Прибавление к какой-нибудь строке
(столбцу) другой её строки (столбца),
умножение на любое число, отличное от нуля.
• Перестановку местами любых двух строк.

9.

3) Метод Крамера
Метод основан на вычислении определителей, поэтому
применим к СЛУ размерности nxn.
Рассмотрим СЛУ:
a11 x1 a12 x2 ... a1n xn b1 ,
a x a x ... a x b ,
21 1
22 2
2n n
2
...........................................
an1 x1 an 2 x2 ... ann xn bn

10.

Введем следующие обозначения:
a11
a11
a1n
, k
an1
ann
Теорема. Если
... b1
a21 ... b2
...
a1n
... a2 n
...
... ... ...
an1
... bn
...
... ann
0, то СЛУ имеет единственное решение
k
xk
, где k 1, n . (Формулы Крамера)

11.

Алгоритм метода:
1) Составим главный определитель - Δ
Δ=
а11 а12 ... a1n
a21 a22 … a2n
.....................
an1 an2 … ann
- определитель системы,
определитель основной матрицы.
2) Составим определитель - Δ1
Δ1 =
b1 а12 ... a1n
b2 a22 … a2n
.....................
bn an2 … ann
- получается из главного определителя
заменой 1-го столбца столбцом
свободных членов.

12.

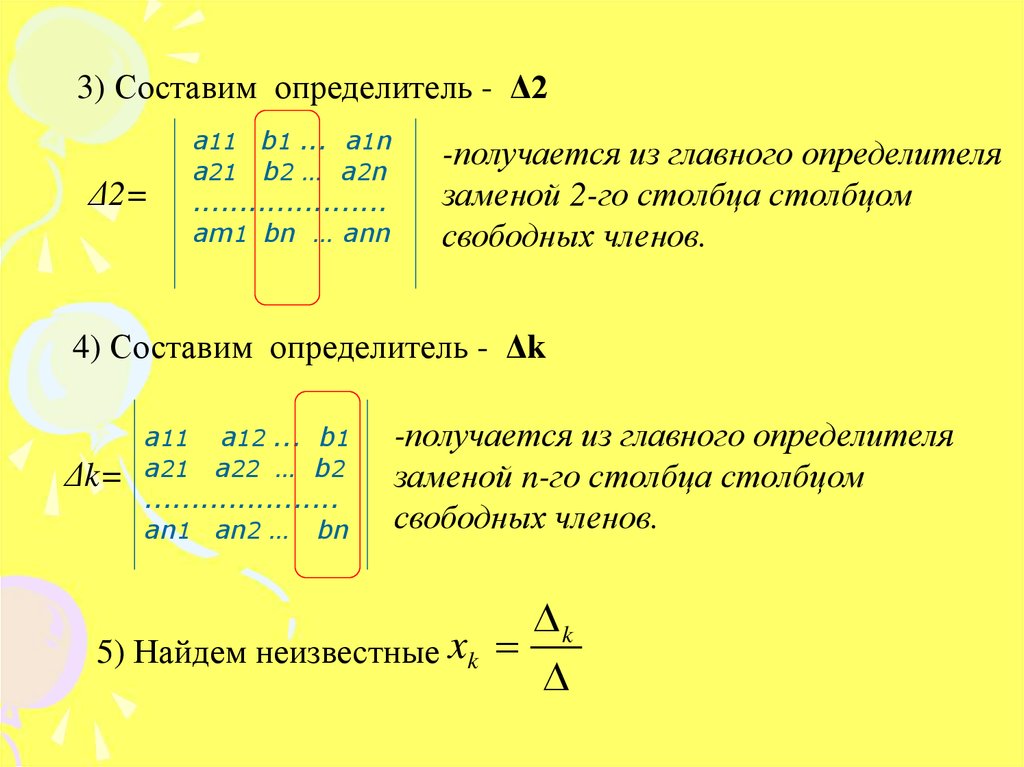
3) Составим определитель - Δ2
Δ2=
а11 b1 ... a1n
a21 b2 … a2n
.....................
am1 bn … ann
-получается из главного определителя
заменой 2-го столбца столбцом
свободных членов.
4) Составим определитель - Δk
Δk=
а11 а12 ... b1
a21 a22 … b2
.....................
an1 an2 … bn
-получается из главного определителя
заменой n-го столбца столбцом
свободных членов.
k
5) Найдем неизвестные xk