Similar presentations:
Случайные величины
1. Случайные величины
2.
O Случайнойвеличиной называется
величина, численное значение которой
может меняться в зависимости от
условий эксперимента.
O Случайные
величины
принято
обозначать
заглавными
буквами
латинского алфавита - X, Y, Z…, а их
значения
–
соответствующими
строчными буквами x, y, z....
3. Пример 1. В вашей группе 17 человек. Случайная величина Х – число студентов, находящихся в аудитории перед началом занятий. Ее
Пример 1. В вашей группе 17 человек.Случайная величина Х – число
студентов, находящихся в аудитории
перед началом занятий.
Ее возможными значениями будут числа
0, 1, 2,…,17.
4. Пример 2. Изменение курса валют.
Пример 2. Изменение курса валют.Случайная
величина
X
стоимость валюты.
Примет некоторое значение
пределах от 57 до 62 рублей.
в
5. Пример 3. Однократное бросание игральной кости.
Пример 3. Однократное бросаниеигральной кости.
Случайная величина X –
число, выпавшее на верхней
грани игрального кубика
Её значения: 1, 2, 3, 4, 5, 6.
6. Пример 4. Случайная величина X -расстояние, которое пролетит снаряд при выстреле из орудия
Возможныезначения
этой
величины
принадлежат некоторому промежутку (a; b).
7.
O Дискретнаяслучайная
величина
–
случайная величина, которая принимает
конечное или счётное число значений с
определенными вероятностями.
O Непрерывная
случайная величина –
случайная
величина,
которая
может
принимать все значения из некоторого
конечного или бесконечного промежутка.
8. Определить вид случайной величины
O Число студентов в группе.O Бросаем игральную кость один раз?
Два раза? n раз?
O Ошибка измерения.
O …
9.
Дискретныеслучайные
величины
(ДСВ)
10.
В денежной лотерее выпущено 100билетов. Разыгрывается один выигрыш в
50 рублей и десять выигрышей по 1
рублю.
Пусть случайная величина Х –
стоимость возможного выигрыша для
владельца одного лотерейного билета.
Найти значения этой величины и
вероятности этих значений.
11.
Запишем возможные значения случайнойвеличины X: x1=50, x2=1, x3=0.
Вычислим вероятность возможных значений
случайной величины Х:
p1=
p2=
p3=1-0,01-0,1=0,89
,
12.
O Можносоставить таблицу соответствий
значений случайной величины и их
вероятностей:
X 0
1
50
P 0,89 0,1 0,01
O Графически решение данной задачи будет
иметь вид:
13.
Соответствиемежду
возможными
значениями
дискретной
случайной
величины и их вероятностями называют
законом распределения дискретной
случайной величины.
14.
15. Числовые характеристики ДСВ
Пусть закон распределения случайнойвеличины Х имеет вид:
X x1 x2 … xn
P p1 p2 … pn
16.
Математическим ожиданием (средним)дискретной случайной величины Х называют
сумму произведений всех ее возможных значений
на их вероятности, т.е. число:
М (X) = х1р1 + х2р2 + … + xnpn.
Свойства математического ожидания:
1
.
M
(
c
)
c
,
c
const
2
.
M
(
x
x
...
x
)
M
(
x
)
M
(
x
)
...
M
(
x
)
1
2
n
1
2
n
3
.
M
(
x
*
x
*
...
*
x
)
M
(
x
)
*
M
(
x
)
*
...
*
M
(
x
)
1
2
n
1
2
n
4
.
M
(
cx
)
cM
(
x
),
c
const
17.
Дисперсией (рассеянием) дискретнойслучайной
величины
называют
математическое
ожидание
квадрата
отклонения случайной величины от ее
математического ожидания:
D(X) = M[X — M(X)]2 = M(X 2) - M 2(X)
Свойства дисперсии:
1
.
D
(
c
)
0
,
c
const
2
2
.
D
(
cX
)
C
D
(
X
)
3
.
D
(
x
x
...
x
)
D
(
x
)
D
(
x
)
...
D
(
x
)
1
2
n
1
2
n
18.
Среднеквадратичное отклонение(X) =
D(X)
19.
Непрерывныеслучайные
величины
(НСВ)
20.
НСВ называется такая величина, возможныезначения которой непрерывно заполняют
некоторый
интервал
(конечный
или
бесконечный).
Число
всех
бесконечно.
возможных
значений
НСВ
Пример: Случайное отклонение по дальности
точки падения снаряда от цели.
21.
Функция распределения НСВФункцией распределения (или интегральной функцией
распределения) называют функцию F(x), определяющую
для каждого значения x вероятность того, что СВХ примет
значение, меньшее х, т.е.
F(x)=P(X<x)
(F(x) определяется и для ДСВ).
Свойства:
1. 0 F(x) 1
2.
3.
4.
P(a x < b) = F(b) F(a)
lim F ( x) 0
x
lim F ( x) 1
x
22. Функция плотности вероятности
O23.
Некоторые законыраспределения
случайных
величин
24. Биномиальное распределение
Дискретная случайнаявеличина X распределена
по биномиальному закону,
если она имеет значения
{0...n}, а вероятность Х=m
P(X=m)=
m
n− m
m
C ∗ p ∗q
n
Биномиальное распределение
описывает вероятность m успехов
при n возможных исходов
M[X]=np - мат. ожидание
D[X]=npq - дисперсия,
где p - вероятность успеха,
q - вероятность неуспеха
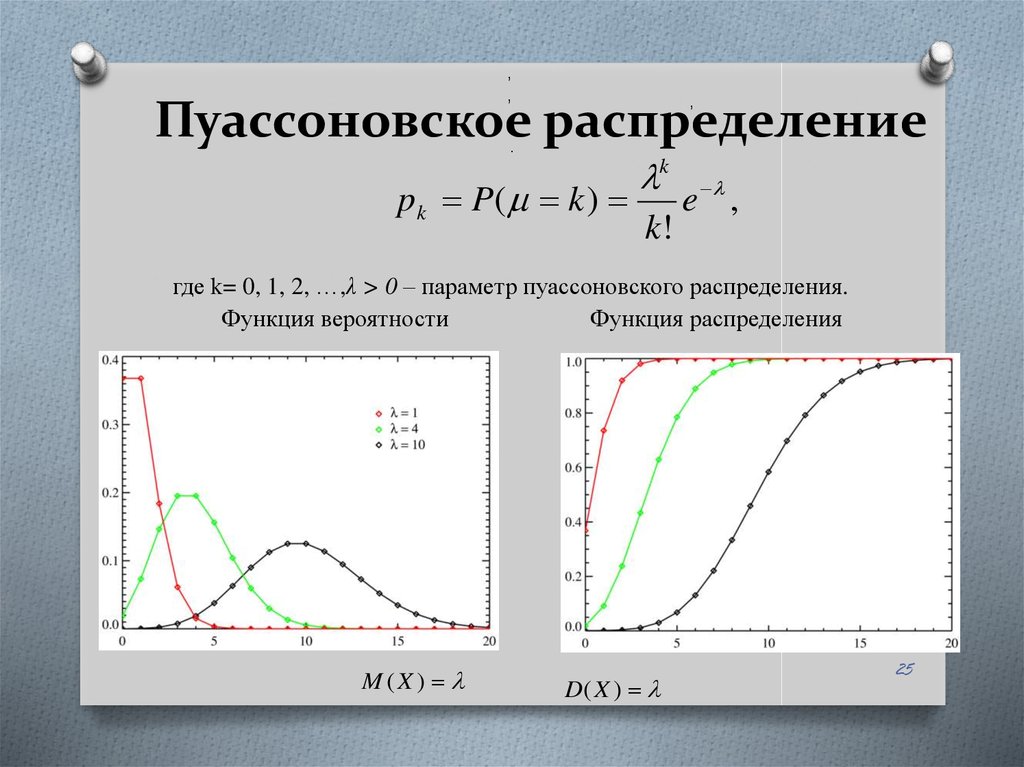
25. Пуассоновское распределение
,,
,
Пуассоновское распределение
.
p k P( k )
k
k!
e ,
где k= 0, 1, 2, …,λ > 0 – параметр пуассоновского распределения.
Функция вероятности
Функция распределения
Основные характеристики
M (X )
D( X )
25
26. Геометрическое распределение
p k P( k ) p k qгде 0 < p < 1,
n,
Функция вероятности
q = 1 – p,
k = 0, 1, …,
Функция распределения
Основные характеристики
1 p
M (X )
p
.
D( X )
q
p2
26
27. Равномерное распределение
Of(x)


























 mathematics
mathematics








