Similar presentations:
Кинетическая и потенциальная энергия, работа, мощность
1.
Лекция 4.1.
2.
3.
4.
Кафедра физики
ПЛАН ЛЕКЦИИ.
Кинетическая энергия, работа, мощность
Потенциальная энергия
Закон сохранения механической энергии
Пример практического применения законов
сохранения. Абсолютно упругий удар.
Общая физика. Раздел "Основы классической механики"
1
2.
Кафедра физикиКИНЕТИЧЕСКАЯ ЭНЕРГИЯ
Запишем уравнение движения (второй закон Ньютона)
для
механической системы из одной частицы
F - результирующая сил, действующих на частицу.
dv
m
F
dt
Умножив скалярно уравнение движения на перемещение частицы
, получим:
ds v dt
dv
m(v )dt ( Fds )
dt
m(v dv ) ( Fds )
Внесем скорость под знак дифференциала, получим:
2
2
v
mv
( Fds )
md d
2
2
Общая физика. Раздел "Основы классической механики"
2
3.
Кафедра физикиКИНЕТИЧЕСКАЯ ЭНЕРГИЯ
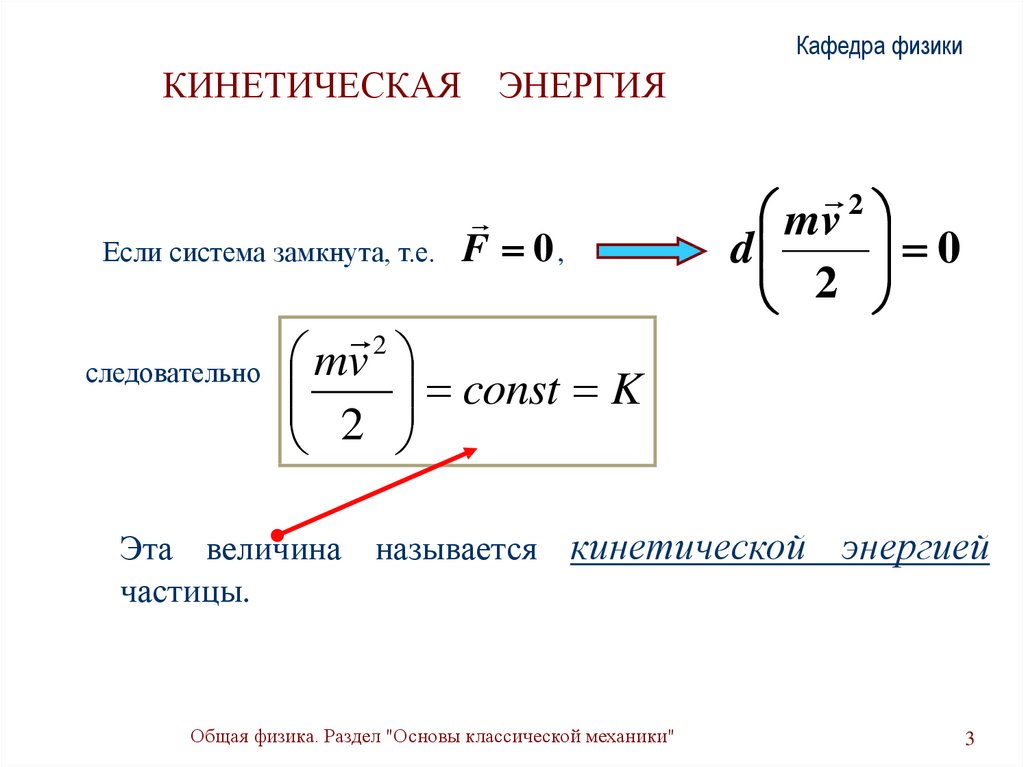
Если система замкнута, т.е.
следовательно
F 0,
2
mv
const K
2
2
mv
0
d
2
Эта величина называется кинетической
частицы.
Общая физика. Раздел "Основы классической механики"
энергией
3
4.
Кафедра физикиРАБОТА.
Если на частицу действует сила
изменяется:
F , кинетическая энергия частицы
mv 2
( Fds )
d
2
В этом случае приращение кинетической энергии частицы за время
.
равно скалярному произведению
Величина dA ( Fds )
ds
пути
записать
( Fds )
dt
F
называется работой, совершаемой силой
на
. Следовательно, раскрыв скалярное произведение можно
dA Fs ds
Работа характеризует изменение энергии, обусловленное действием
силы на движущуюся частицу. Иначе, работу совершает только сила.
Общая физика. Раздел "Основы классической механики"
4
5.
6.
dA ( F dS ) F cos dS .РАБОТА.
.
F
2
cos 0 dA 0,
dS
FS
.
2
cos 0 dA 0,
2
.
cos 0 dA 0,
Общая физика. Раздел "Основы классической механики"
6
7.
РАБОТА. Физический смыслFS
Проинтегрируем соотношение
dA
mv2
Fs ds
d
2
FS
1
2 S
dS
mv
1 d 2
2
2
Fs ds
1
2
вдоль некоторой траектории от точки 1
до точки 2:
2
2
2
mv2
mv1
Fs ds
2
2
1
K2 K1 A
Работа результирующей всех сил, действующих на
частицу, идет на приращение кинетической энергии
частицы
Общая физика. Раздел "Основы классической механики"
7
8.
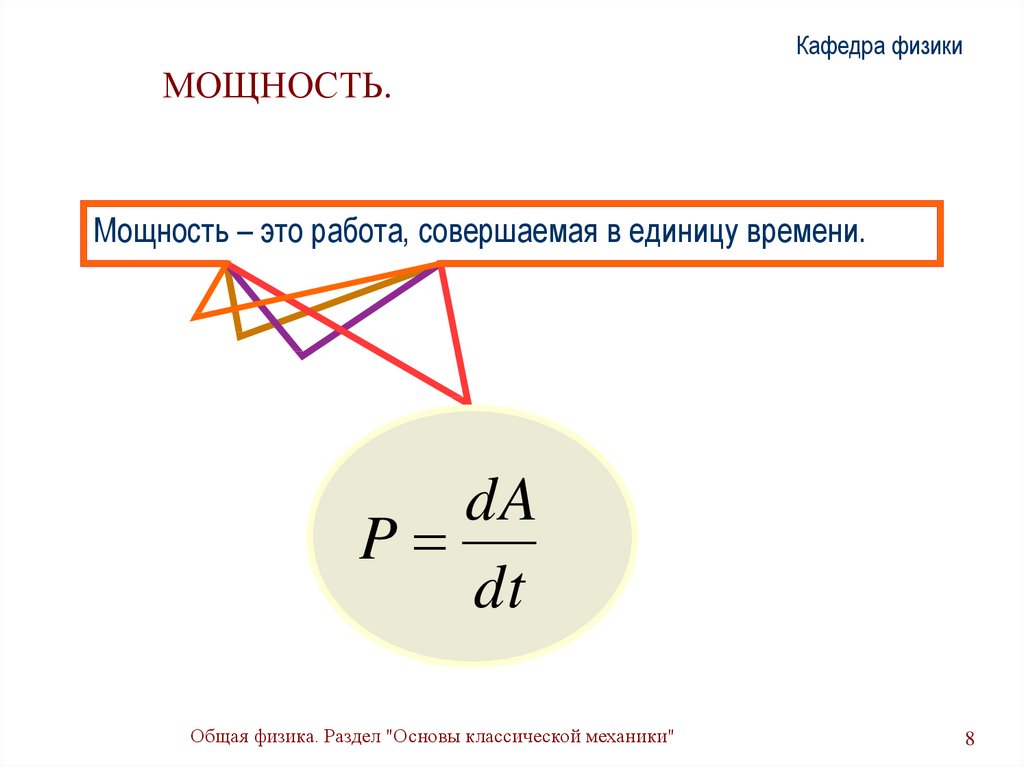
Кафедра физикиМОЩНОСТЬ.
Мощность – это работа, совершаемая в единицу времени.
dA
P
dt
Общая физика. Раздел "Основы классической механики"
8
9.
Кафедра физикиПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ
Силовые поля делятся на потенциальные и непотенциальные
Силовое поле , работа которых зависит только от начального и
конечного положения тела, но не от траектории его перемещения.
Такие силы называются консервативными или потенциальными.
Поле сил притяжения или гравитационное поле. Сила тяжести.
Fтяж P mg
Общая физика. Раздел "Основы классической механики"
9
10.
Кафедра физикиПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ
Потенциальная энергия W р — скалярная физическая величина,
представляющая собой часть полной механической энергии
системы, находящейся в поле консервативных сил. Зависит от
положения материальных точек, составляющих систему, и
характеризует работу, совершаемую полем при их перемещении
Работа консервативной силы А12 равна изменению потенциальной
энергии частицы, взятому с обратным знаком.
A12 (W p2 W p1 ) (W p1 W p2 )
Общая физика. Раздел "Основы классической механики"
10
11.
Кафедра физикиПотенциальная энергия поля силы тяжести
Определим вид функции W p для частицы в поле сил тяжести
dA12 ( Pds ) mgds у
A12 mgds у mgl mg h1 h2
2
1
1
ds
h1
A12 W p1 W p2
l h1 h2
ds у
P mg
W mgh
h2
2
у
Общая физика. Раздел "Основы классической механики"
11
12.
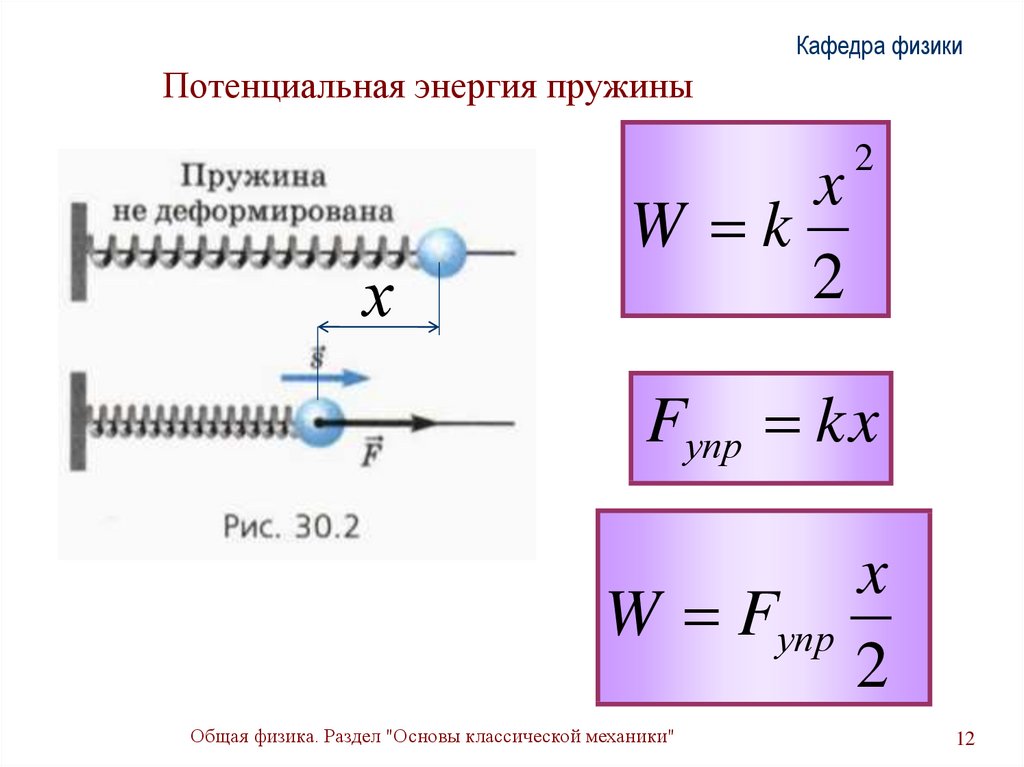
Кафедра физикиПотенциальная энергия пружины
х
x
W k
2
2
Fупр kx
W Fупр
Общая физика. Раздел "Основы классической механики"
x
2
12
13.
Закон сохранения полной механической энергииПолная механическая энергия системы Е - сумма кинетической
К и потенциальной W энергии тел, составляющих замкнутую
систему и взаимодействующих между собой посредством
консервативных сил (сил тяготения и сил упругости) остается
неизменной.
.
14.
Кафедра физикиЗАКОНЫ СОХРАНЕНИЯ. Пример практического применения
Абсолютно упругий удар
Абсолютно упругим называется такой удар, при котором
механическая энергия тел не переходит в другие,
немеханические, виды энергии.
Абсолютно неупругий удар - кинетическая энергия тел
частично или полностью превращается во внутреннюю
энергию; после удара столкнувшиеся тела движутся с
одинаковой скоростью, либо покоятся.
Рассмотрим абсолютно упругий удар двух однородных частиц,
образующих замкнутую систему
Общая физика. Раздел "Основы классической механики"
14
15.
Кафедра физикиЗАКОНЫ СОХРАНЕНИЯ. Пример практического применения
m1
v10
m2
v20
m2
m1
v1
v2
Скорости шаров до взаимодействия v10 и v20 после соударения
v1 и v2 -
Запишем законы сохранения энергии и импульса:
2
2
m1v10
m2v20
m1v12 m2v22
2
2
2
2
m1v10 m2v20 m1v1 m2v2
Общая физика. Раздел "Основы классической механики"
(3.1)
(3.2)
15
16.
Кафедра физикиЗАКОНЫ СОХРАНЕНИЯ. Пример практического применения
Преобразуем выражение (3.1) (a 2 b 2 a b a b ):
m1 v10 v1 v10 v1 m2 v2 v20 v2 v20
(3.3)
Выражение (3.2) запишем в виде:
m1v10 m2v20 m1v1 m2v2
m1 v10 v1 m2 v2 v20
v10 v10 , v20 v20 , v1 v1 , v1 v2
(3.4)
Скорости шаров до после удара будут направлены вдоль одной
прямой, следовательно, векторы в соотношениях (3.3) и (3.4)
коллинеарные (направлены вдоль параллельных прямых)
Общая физика. Раздел "Основы классической механики"
16
17.
Кафедра физикиЗАКОНЫ СОХРАНЕНИЯ. Пример практического применения
После преобразований получим:
2m2v20 m1 m2 v10
v1
m1 m2
2m1v10 m1 m2 v20
v2
m1 m2
Общая физика. Раздел "Основы классической механики"
17














 physics
physics








