Similar presentations:
Тригонометрические формулы и функции
1. Повторение: «Тригонометрические формулы и функции»
Урок вводного повторенияв 11 классе
Подготовила Г.В. Цуканова
2.
Определение тригонометрическихфункций
y
Если M (t) = M (x; y), то
y sin t
–1
1 cos t 1 1 sin t 1
sin t
tgt
, t k,
cos t
2
cos t
ctgt
, t k,
sin t
cost
1
+
+
–
+
M (t)
1 x
–1
y
tgt , ctgt
–
+
x cos t ,
+
–
–
–
sint
+
–
x
3.
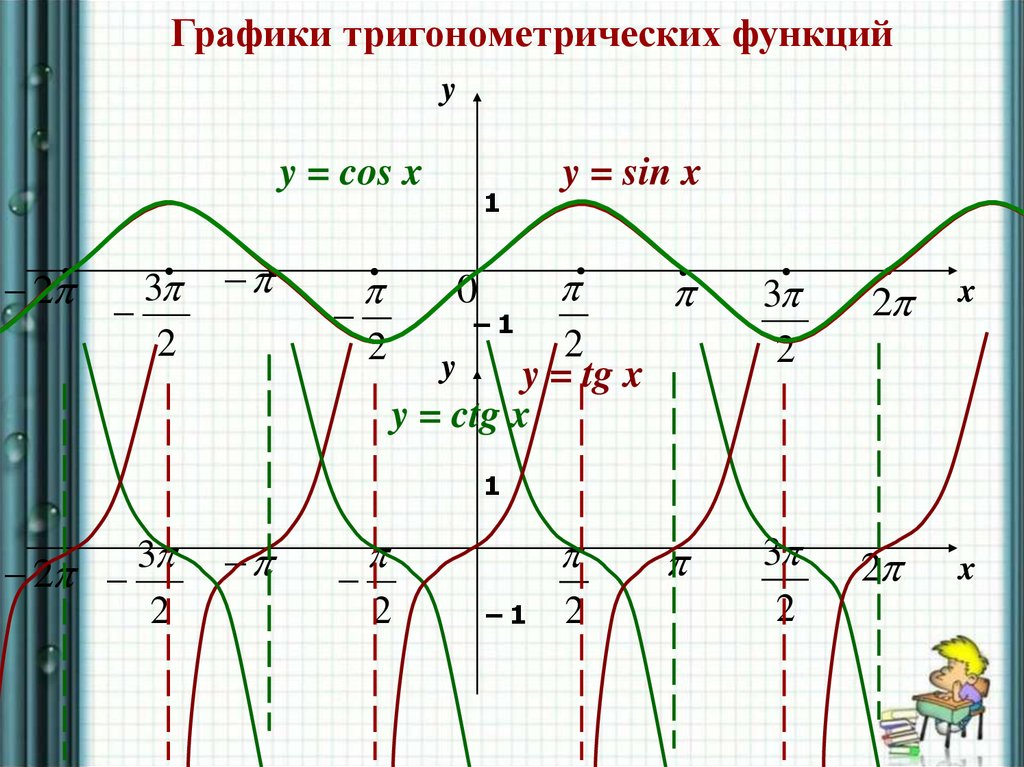
Графики тригонометрических функцийy
y = cos x
2
3
2
1
y = sin x
–1
2
2 y
y = tg x
y = ctg x
0
3
2
2
3
2
2
x
1
3
2
2
2
–1
2
x
4.
Основные тригонометрическиеформулы
sin t cos t 1,
2
2
sin t
tgt
, t k, k Z
cos t
2
cos t
ctgt
, t k, k Z
sin t
1
1 tg t
, t k, k Z
2
cos t
2
2
1
1 ctg t
, t k, k Z
2
sin t
2
5.
Формулы двойного аргументаsin 2 x 2sin x cos x
cos 2 x cos x sin x
2
2
cos 2 x 2cos x 1 1 2sin x
2
2
Формулы понижения степени
1 cos 2 x
2
sin x
2
1 cos 2 x
cos x
2
2
6.
Связь между тригонометрическимифункциями углового и числового аргумента
180
6
30
2
90
3
60
4
3
270
2
2
120 120
180 3
180
22,5
8 8
45
7.
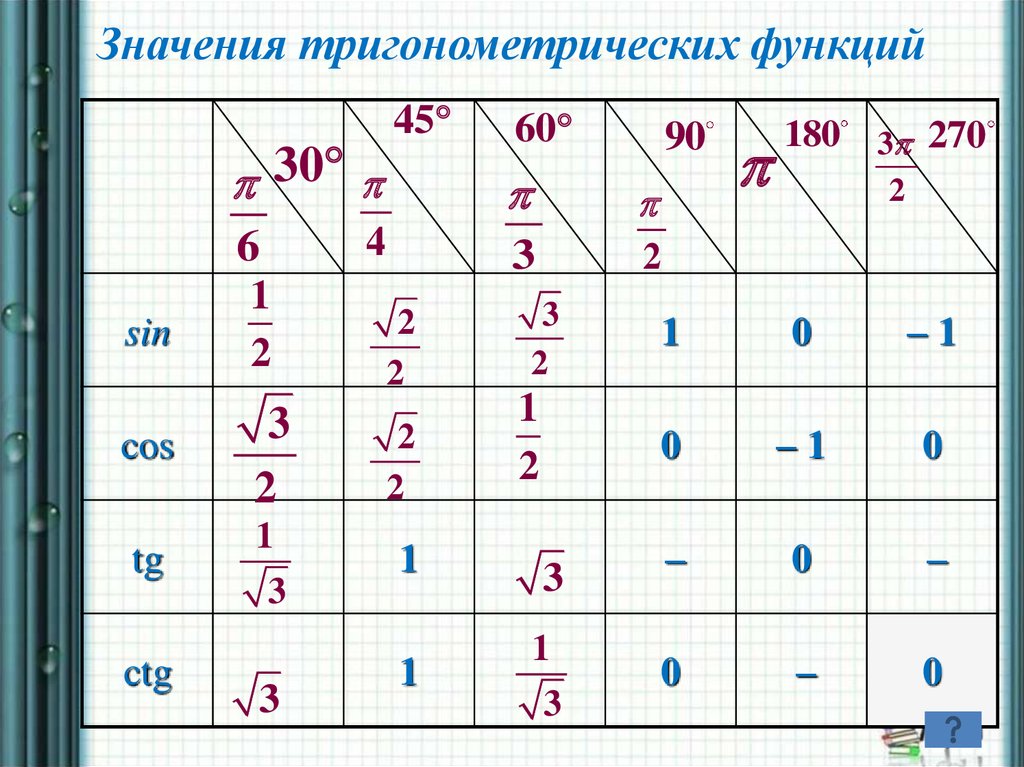
Значения тригонометрических функций45
30
4
3
6
sin
1
2
cos
3
2
2
2
tg
1
3
1
ctg
60
3
2
2
1
90
2
3
2
1
2
3
1
3
180 3 270
2
1
0
–1
0
–1
0
–
0
–
0
–
0
8.
34 • 2
5
4
2
4
2
2
2
0
2
2 2
2 • 7
3
2
4
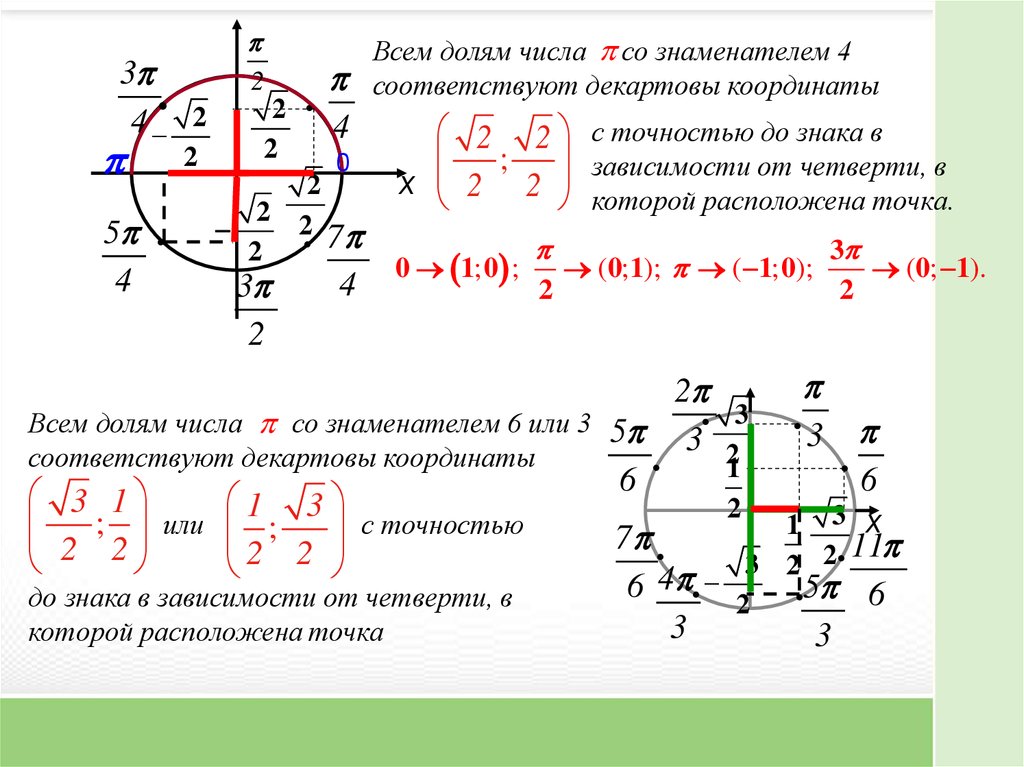
Всем долям числа со знаменателем 4
соответствуют декартовы координаты
2 2 с точностью до знака в
;
зависимости от четверти, в
х 2 2 которой расположена точка.
0 1; 0 ;
2
(0;1); ( 1; 0);
3
(0; 1).
2
2
• 3
Всем долям числа со знаменателем 6 или 3 5
•3
3
21
соответствуют декартовы координаты
6
6
3 1
1 3
2
;
или
с
точностью
1 3 х
;
7
11
2
2
2
2
2
3
2
6 4 • 2 •5 6
до знака в зависимости от четверти, в
3
которой расположена точка
3
9.
Формулы приведенияЕсли под знаком тригонометрической функции выражение вида:
3
5
;
;
2
2
2
и т. д., то функция меняется на
родственную;
Если ; 2 ; 3 и т. д., то функция не меняется.
И в любом случае проверяем знак той функции, которая была
задана.






 mathematics
mathematics








