Геометрия в ЛОГО

1. Геометрия в ЛОГО

Районная конференция
«Шаг в науку»
Геометрия в ЛОГО
Выполнила:
ученица 5 класса
МБОУ Софпорогская основная
школа
Булгакова Вероника.
Руководитель:
Лобова Анна Владимировна,
учитель математики и
информатики
п. Лоухи, 2017 год

2. Объект моего исследования

3. Гипотеза

• Черепашка рисует
геометрические фигуры не
случайным образом, этому есть
геометрическое обоснование.

4. Исследовательские задачи

• Изучить геометрию углов
правильных многоугольников и
выявить их некоторые свойства;
• доказать или опровергнуть гипотезу
своего исследования.

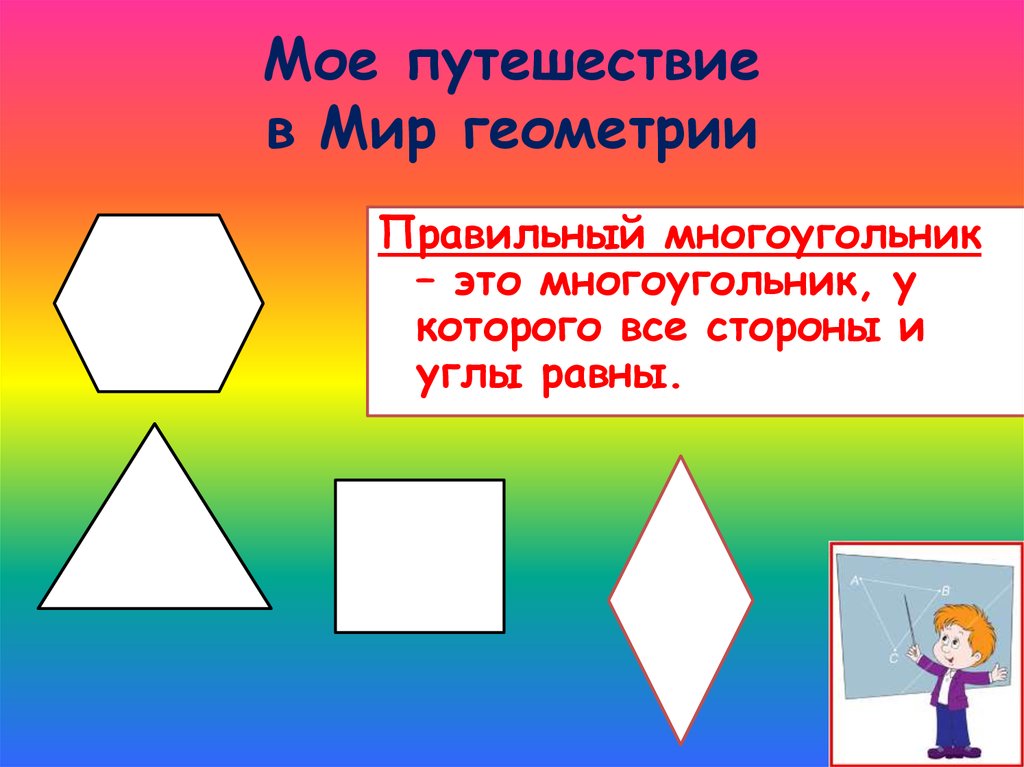
5. Мое путешествие в Мир геометрии

Правильный многоугольник
– это многоугольник, у
которого все стороны и
углы равны.

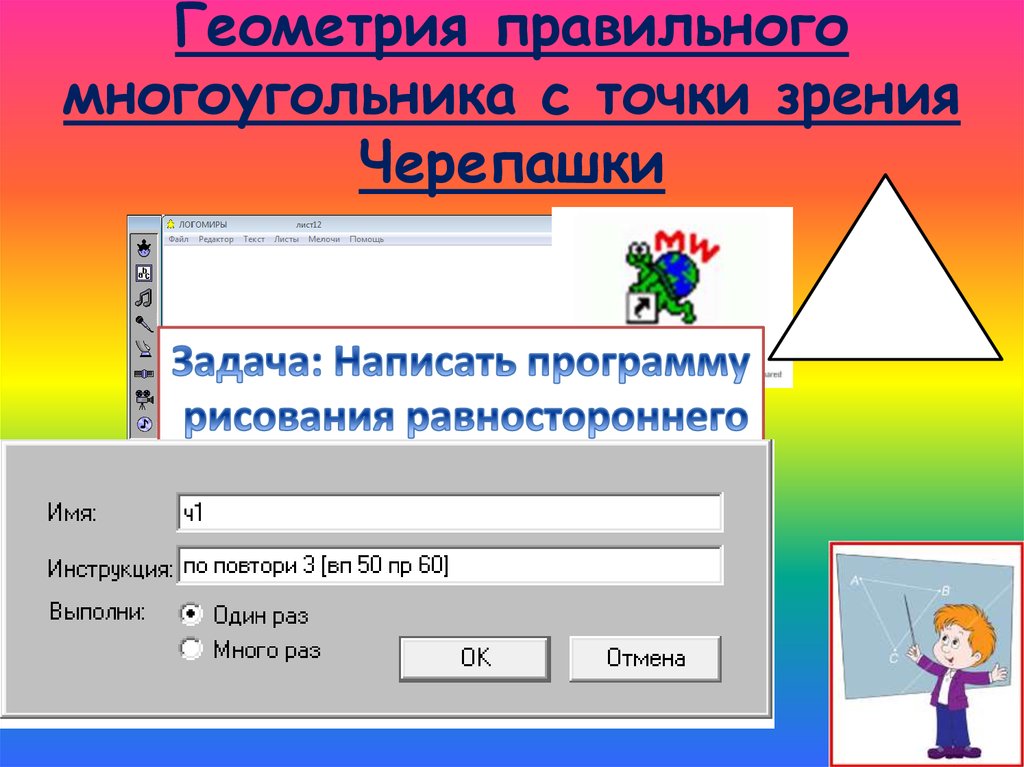
6. Геометрия правильного многоугольника с точки зрения Черепашки

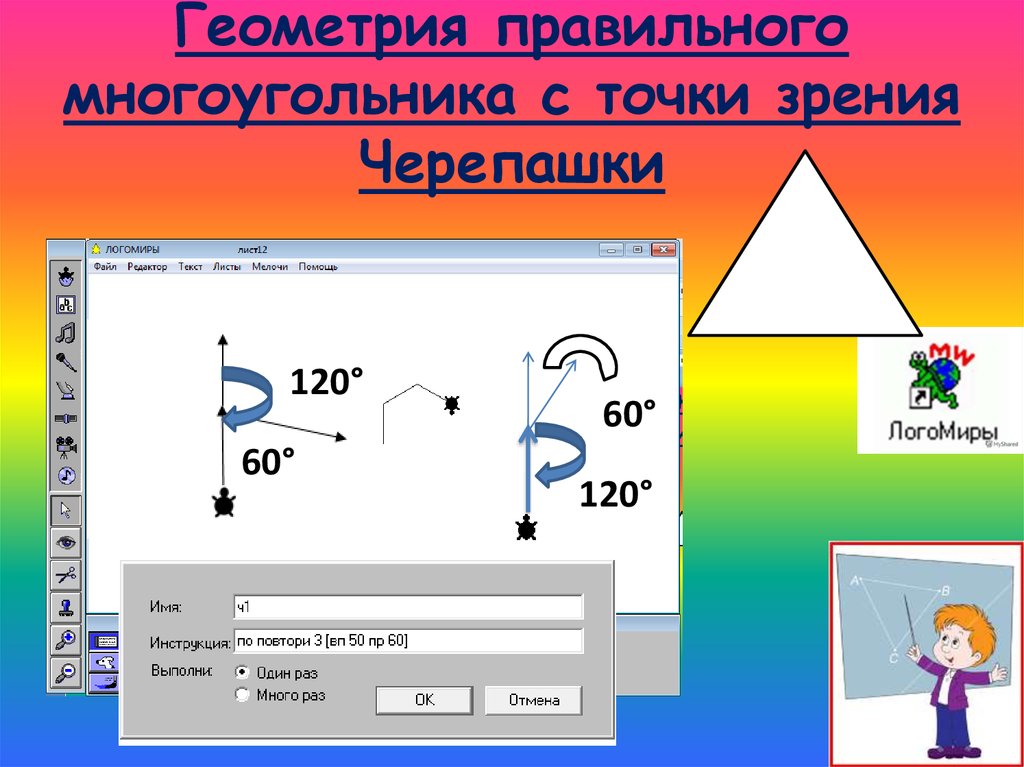
7. Геометрия правильного многоугольника с точки зрения Черепашки

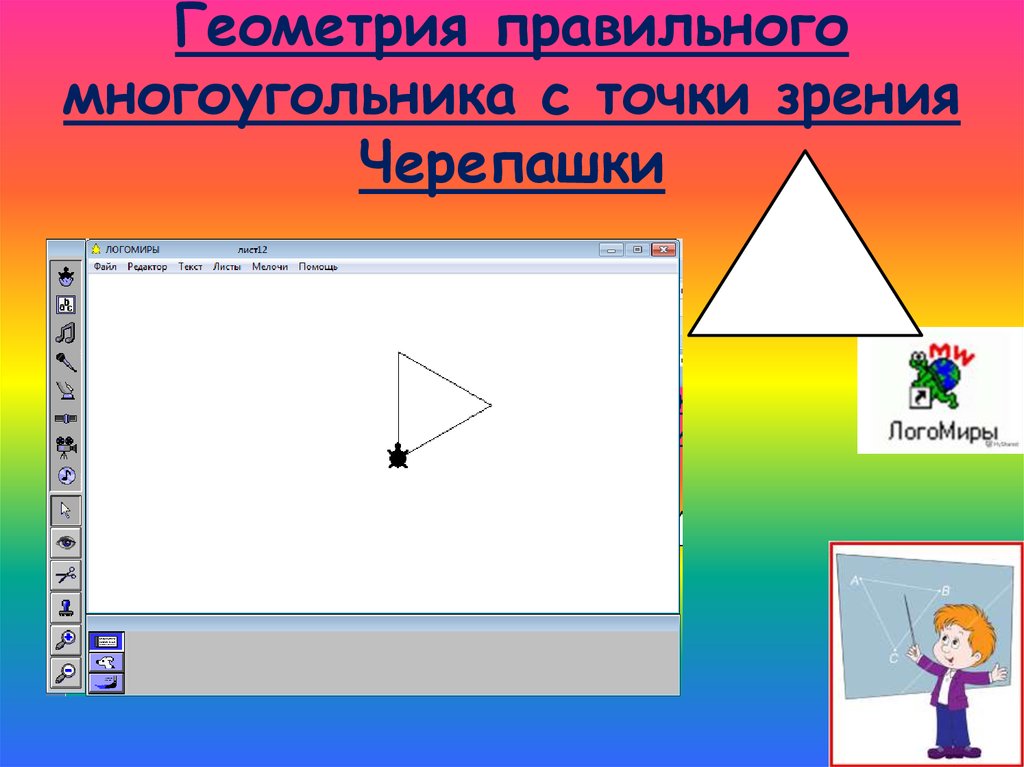
8. Геометрия правильного многоугольника с точки зрения Черепашки

120°
60°
60°
120°

9. Геометрия правильного многоугольника с точки зрения Черепашки

10. Геометрия правильного многоугольника с точки зрения Черепашки

11. Геометрия правильного многоугольника с точки зрения Черепашки

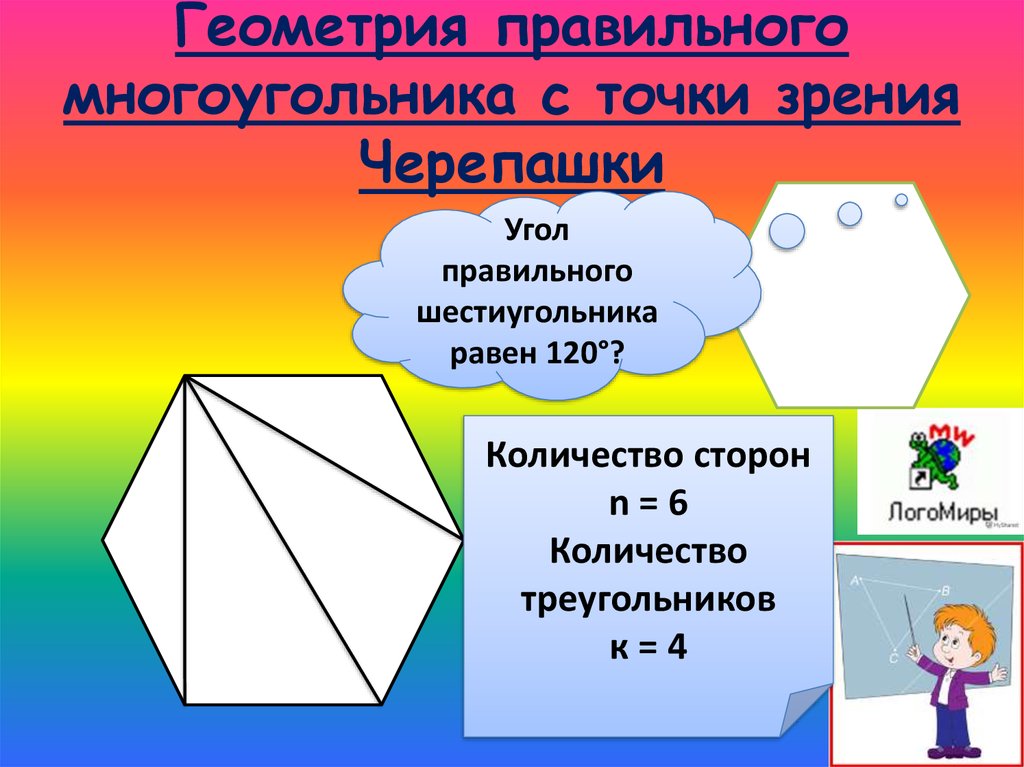
Угол
правильного
шестиугольника
равен 120°?

12. Геометрия правильного многоугольника с точки зрения Черепашки

Угол
правильного
шестиугольника
равен 120°?

13. Геометрия правильного многоугольника с точки зрения Черепашки

Угол
правильного
шестиугольника
равен 120°?
Количество сторон
n=6
Количество
треугольников
к=4

14. Геометрия правильного многоугольника с точки зрения Черепашки

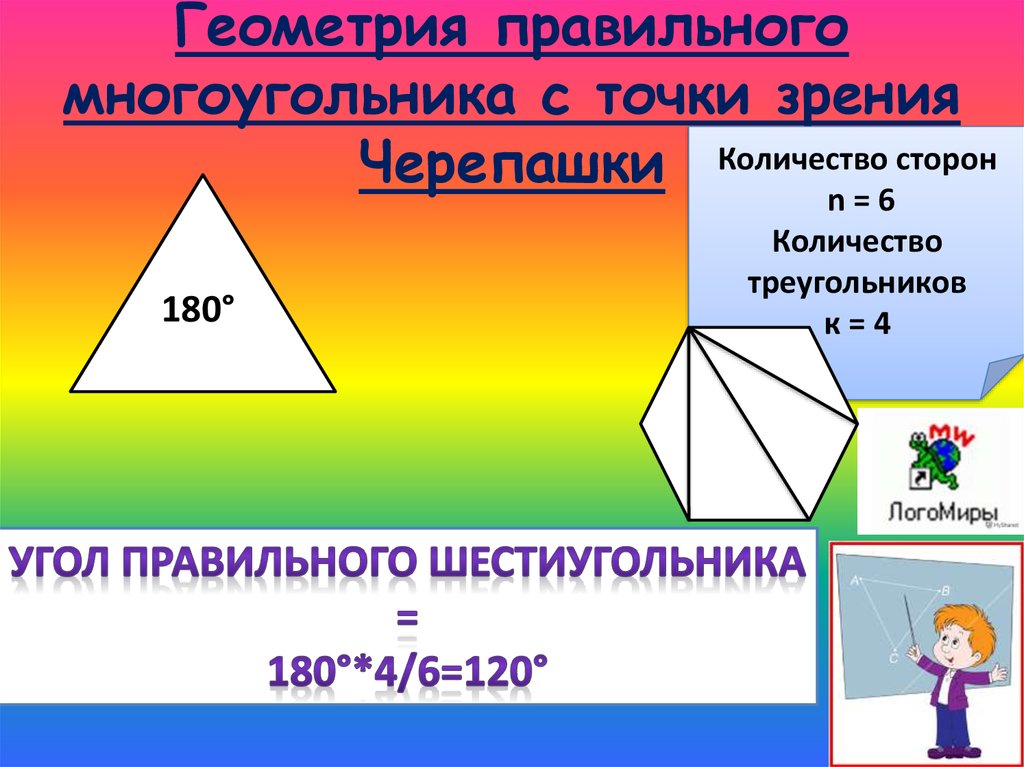
Количество сторон
180°
n=6
Количество
треугольников
к=4

15. Геометрия правильного многоугольника с точки зрения Черепашки

Количество сторон
n=5
Количество
треугольников
к=3

16. Геометрия правильного многоугольника с точки зрения Черепашки

Эксперимент для правильных
многоугольников с
количеством сторон n=3…20
Показал, что любой угол
правильных многоугольников
можно рассчитать по формуле:
180*к/n

17. Геометрия правильного многоугольника с точки зрения Черепашки в задачах ОГЭ по информатике

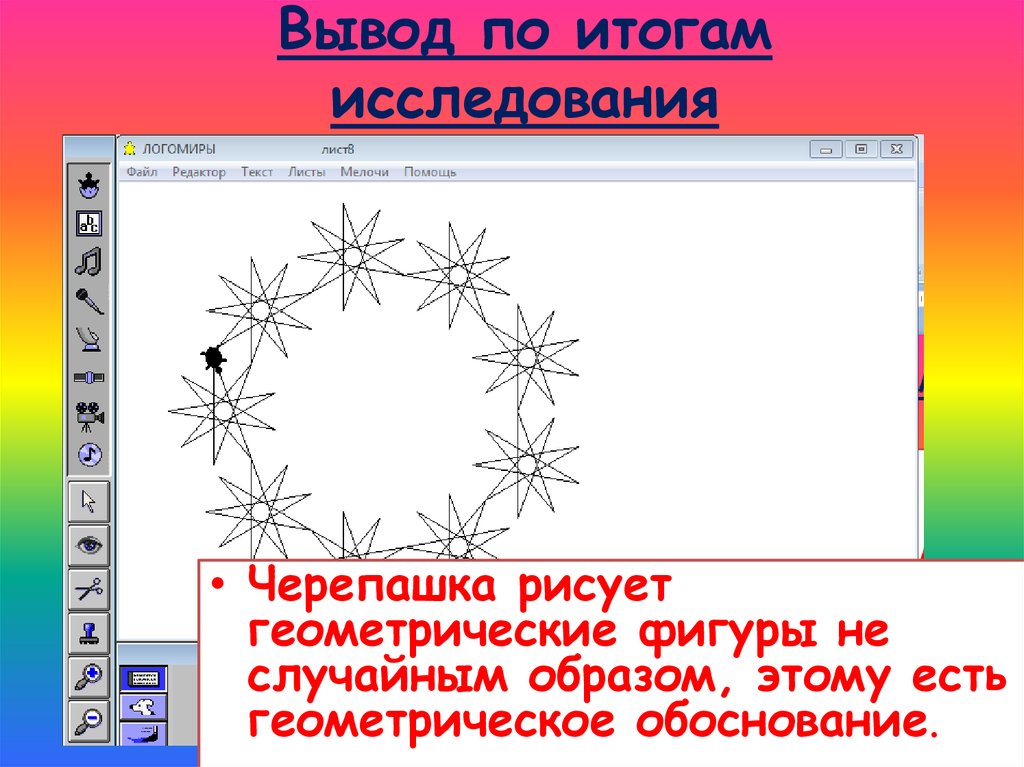
18. Вывод по итогам исследования

• Черепашка рисует
геометрические фигуры не
случайным образом, этому есть
геометрическое обоснование.

19. Моя «Геометрическая мозаика» как творческий итог моего исследования

• В основе Мозаики лежат процедуры
построения правильных многоугольников
с количеством сторон от n=3 до n=20.
• В листе написания программ я провела
эксперимент и поворачивала правильные
многоугольники на