Similar presentations:
Центральные и вписанные углы
1.
ГБОУ СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА № 1909Имени Героя Советского Союза А.К.Новикова
Проект:
«Центральные
и вписанные углы»
Работа ученика
ГБОУ СОШ № 1909
Семенова Виктора
Учитель:
Пакульских Елена
Валентиновна
2.
D Дуга-это часть окружности,заключённая между двумя
точками.
А
О
АВ - дуга
АСB , АДВ - дуги
C
B
если АВ - диаметр , то
АСВ – полуокружность,
АДВ – полуокружность.
3.
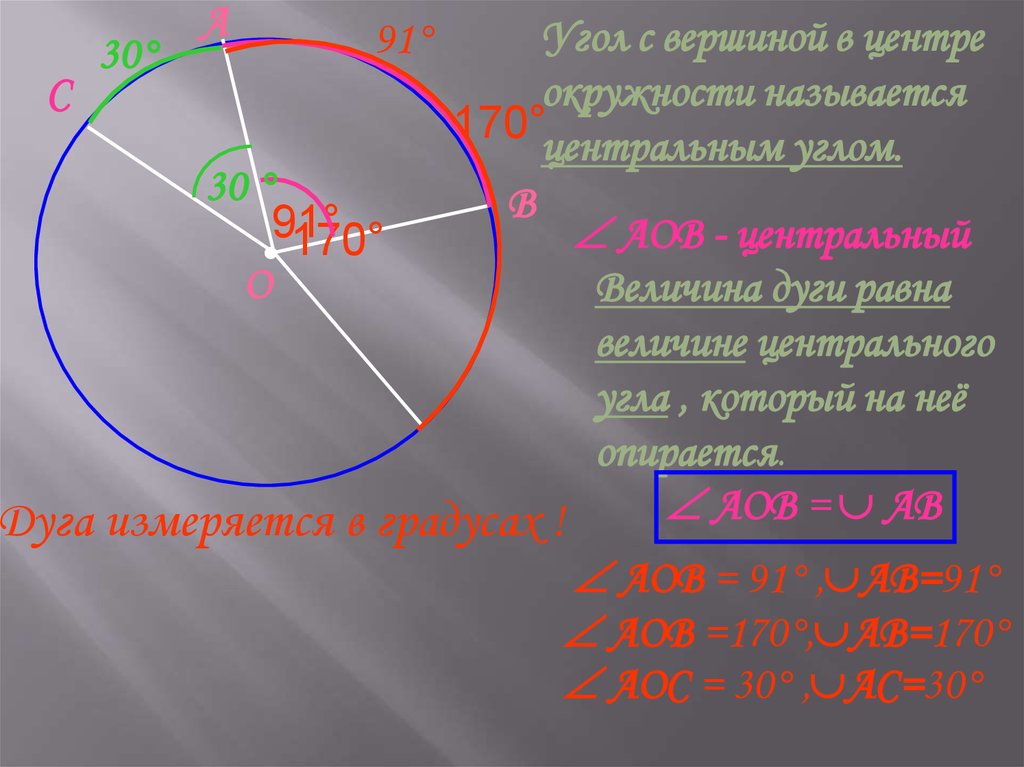
АУгол с вершиной в центре
окружности называется
С
170°центральным углом.
30 °
В
91°
АОВ - центральный
● 170°
О
Величина дуги равна
величине центрального
угла , который на неё
опирается.
АOВ = АВ
Дуга измеряется в градусах !
30°
91°
АOВ = 91° , АВ=91°
АOВ =170°, АВ=170°
АOС = 30° , АС=30°
4.
АC
О
Угол наз-ся вписанным,
если его вершина лежит
на окружности, а
стороны пересекают
окружность.
АBС-вписанный
Вписанный угол измеряется
B
половиной дуги, на которую он
опирается.
АВС=½· АС или АВС=½ · АОС
5.
C3
2
B
Дано: Окр(О;r) ;
А АВС-вписанный;
АОС-центральный.
Доказать:
4
АВС=½ АОС
1 ●О
Доказательство:
1) АОВ-развёрнутый,
═> 1=180˚- 4
2) ∆BOC-р/б, 2= 3,
1=180˚-( 2+ 3)
1=180˚-2· 2
2· 2= 4 ═> 2= ½ 4
АВС=½ · АОС или АВС=½ АС,
ч.т.д.
6.
C4
О
3
B
1
2
Дано: Окр(О;r) ;
АВС-вписанный;
АОС-центральный.
Доказать:
АВС=½ АОС
А
Доказательство:
+
1= ½· 2
3=½· 4
1+ 3=½· ( 2+ 4)
ABC=½· AOC, ч.т.д.
7.
21
3
4
A
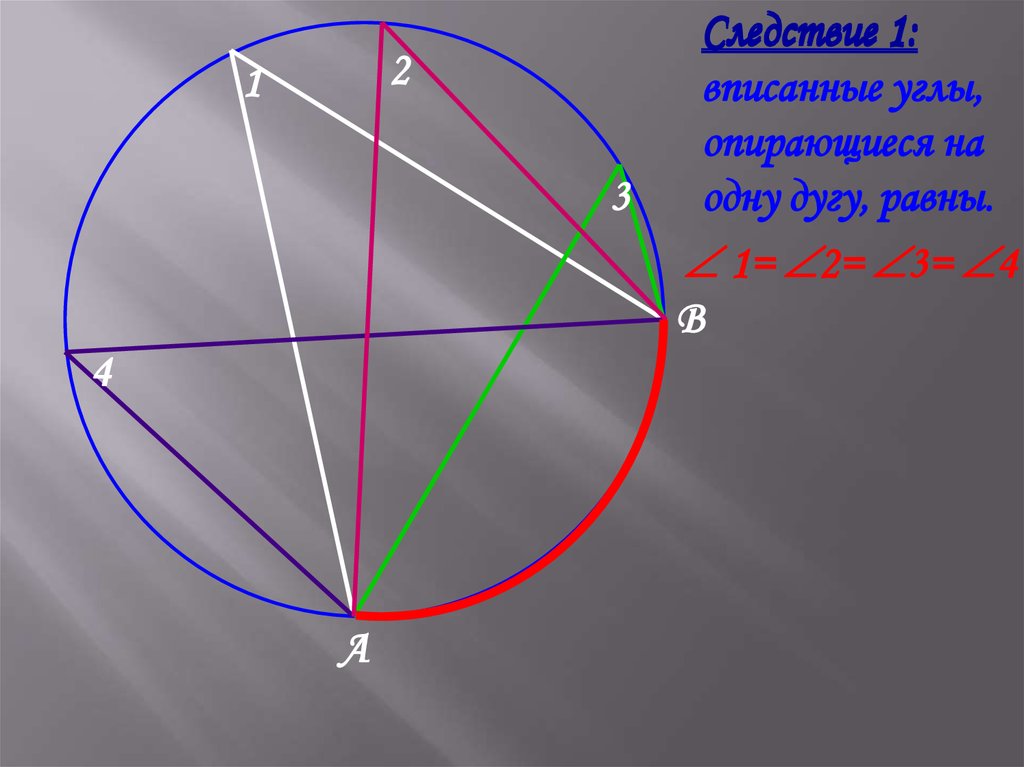
Следствие 1:
вписанные углы,
опирающиеся на
одну дугу, равны.
1= 2= 3= 4
B
8.
FA
F
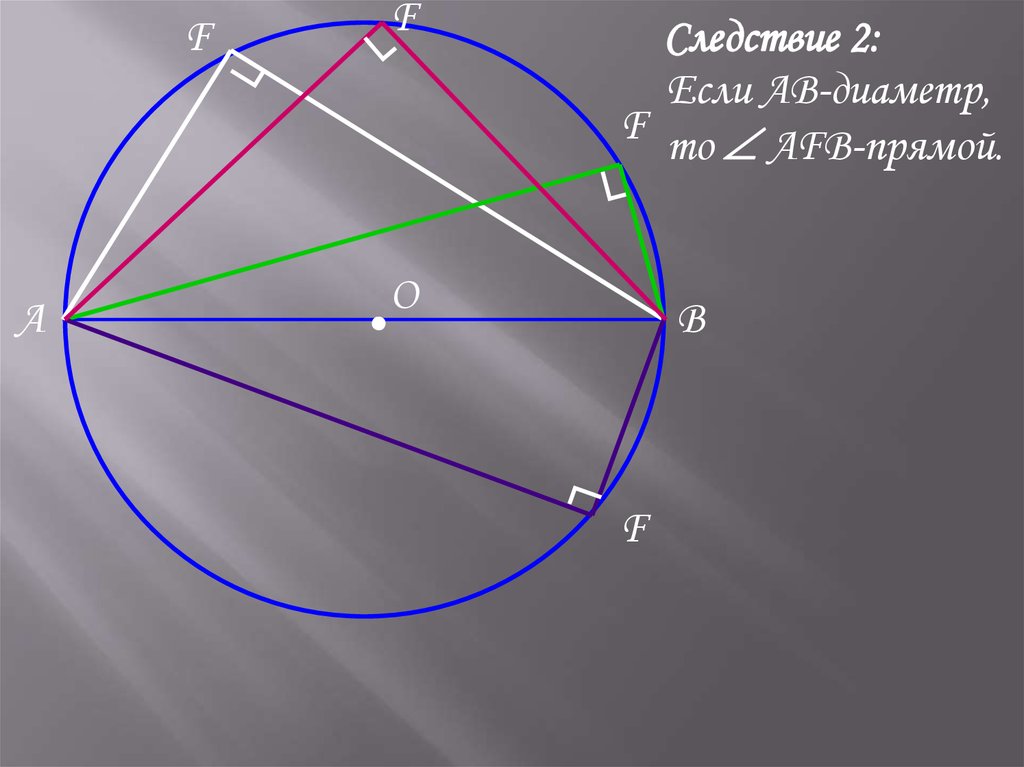
Следствие 2:
Если АВ-диаметр,
F то AFB-прямой.
О
B
F
9.
Какой это угол ?О
10.
zα
40˚
30˚х
120˚ y
Х=120˚:2=60˚
y=40˚·2=80˚
Z=30˚
α=90˚
11.
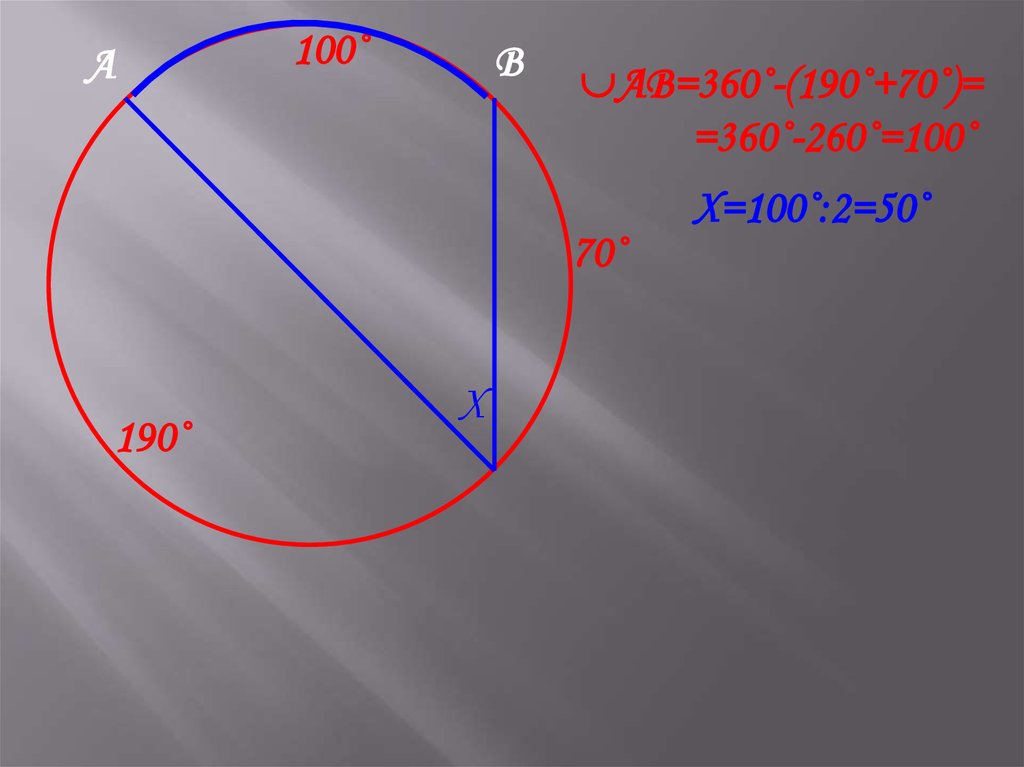
А100˚
В
АВ=
АВ=360˚-(190˚+70˚)=
=360˚-260˚=100˚
70˚
190˚
Х
Х=100˚:2=50˚
12.
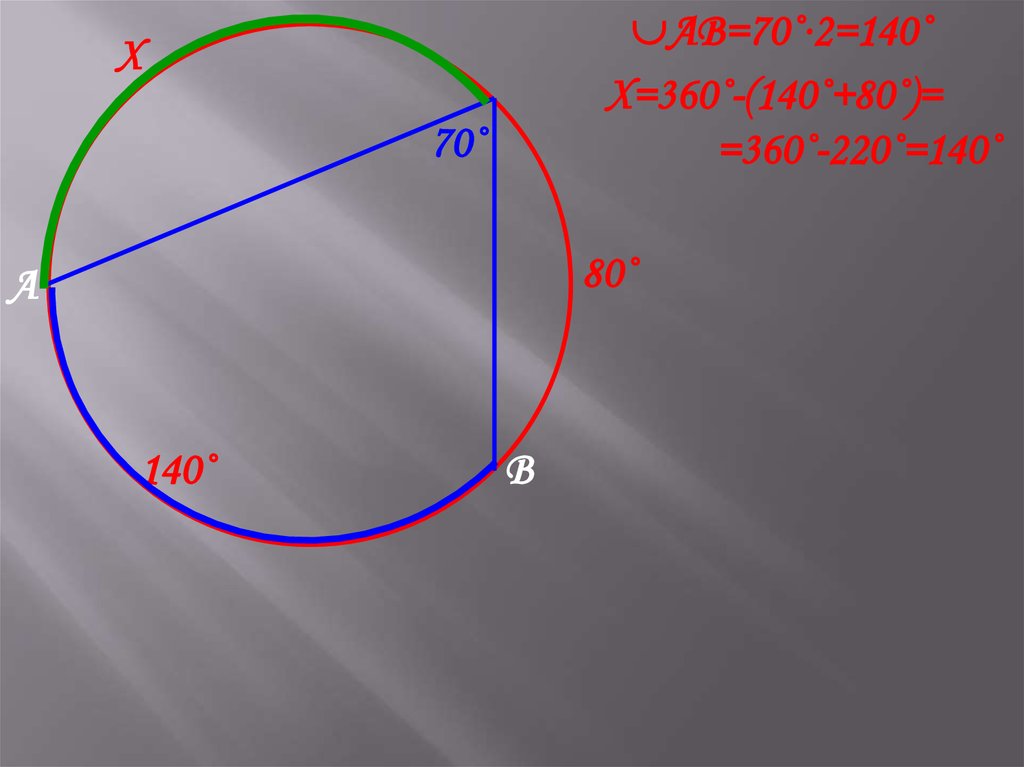
АВ=70˚∙2=140˚АВ
Х=360˚-(140˚+80˚)=
=360˚-220˚=140˚
Х
70˚
80˚
А
140˚
В
13.
ХВ
АВ =180˚
90˚
Х=180˚-130˚=50˚
О
130˚
А
180˚








 mathematics
mathematics








