Similar presentations:
Квадратичная функция и ее свойства
1. ТЕМА УРОКА:
2. Цели урока:
ЦЕЛИ УРОКА:обобщить, систематизировать и закрепить
знания по данной теме;
формировать навыки использования
полученных ранее знаний;
развивать логическое мышление,
наблюдательность, внимание.
3. 1 этап
1 ЭТАП4. 1. Дайте определение квадратичной функции
1. ДАЙТЕ ОПРЕДЕЛЕНИЕ КВАДРАТИЧНОЙФУНКЦИИ
у
0
Определение:
х
у
0
Функция вида у = ах2 + bx + с,
где а, b, c – заданные числа, а≠0,
x – действительная переменная,
называется квадратичной функцией.
х
5. 2. Найдите значение квадратичной функции
2. НАЙДИТЕ ЗНАЧЕНИЕ КВАДРАТИЧНОЙФУНКЦИИ
-2
5102
6. 3. Найдите нули функции
3. НАЙДИТЕ НУЛИ ФУНКЦИИу
1
0
1
2
х
7.
у1
-3
-1
0
1
х
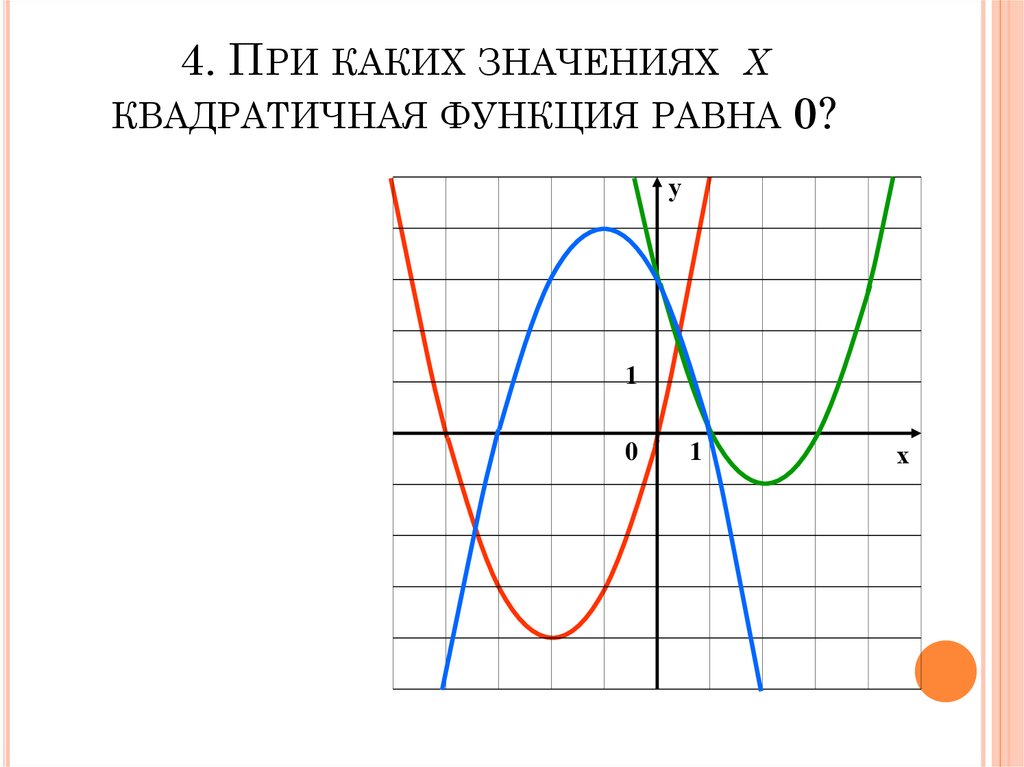
8. 4. При каких значениях x квадратичная функция равна 0?
4. ПРИ КАКИХ ЗНАЧЕНИЯХ XКВАДРАТИЧНАЯ ФУНКЦИЯ РАВНА
0?
у
1
0
1
х
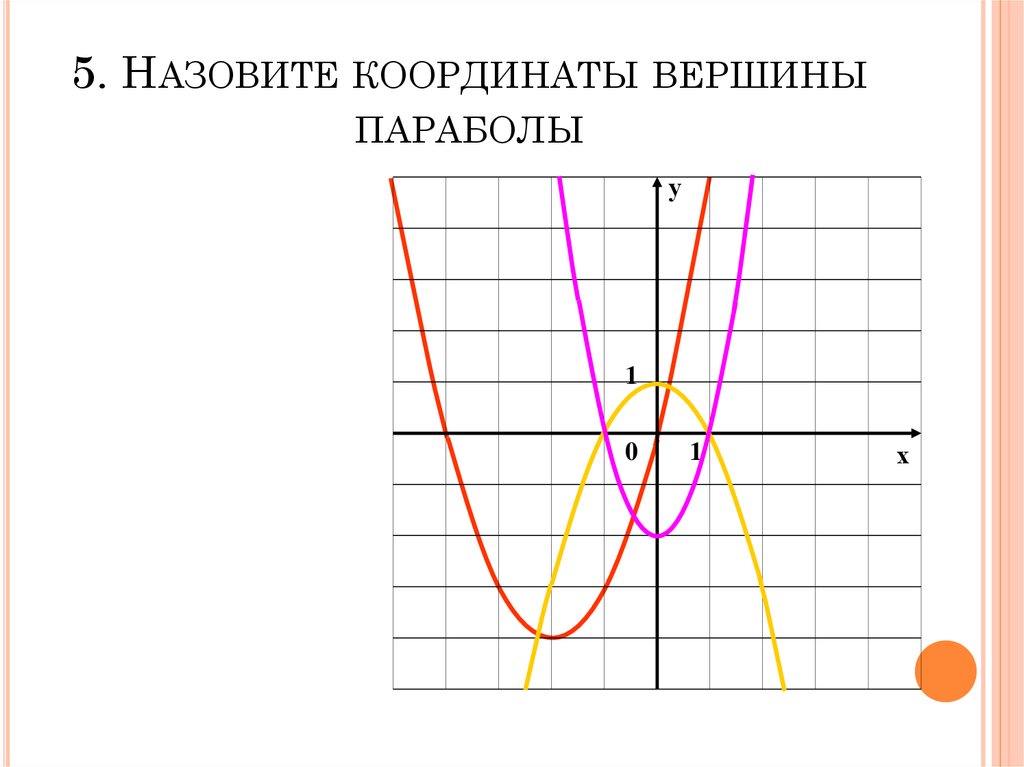
9. 5. Назовите координаты вершины параболы
5. НАЗОВИТЕ КООРДИНАТЫ ВЕРШИНЫПАРАБОЛЫ
у
1
0
1
х
10. 2 этап
2 ЭТАП11.
ПРИГОТОВЬТЕСЬ К ОТВЕТУ НА ЭТИ ЖЕВОПРОСЫ В АВТОМАТИЧЕСКОМ РЕЖИМЕ
ПОКАЗА СЛАЙДОВ
12. Найдите значение квадратичной функции
НАЙДИТЕ ЗНАЧЕНИЕ КВАДРАТИЧНОЙФУНКЦИИ
-2
1502
.
23415
13. Найдите нули функции
НАЙДИТЕ НУЛИ ФУНКЦИИ6
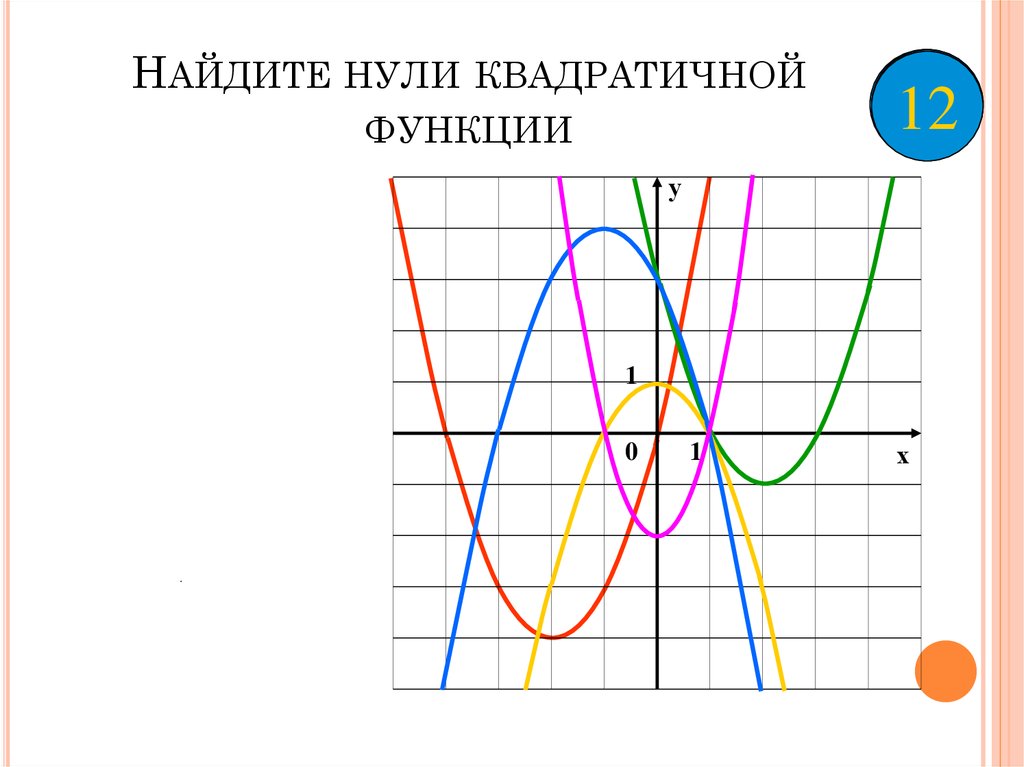
14. Найдите нули квадратичной функции
НАЙДИТЕ НУЛИ КВАДРАТИЧНОЙФУНКЦИИ
10
89
11
12
у
1
0
.
.
1
х
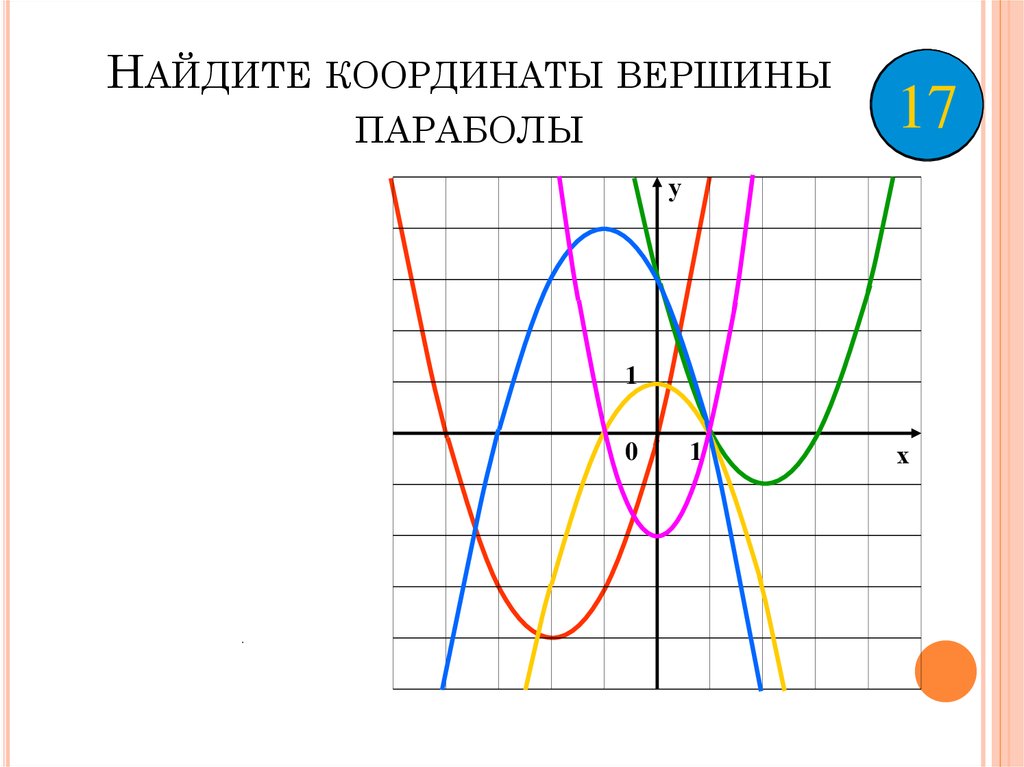
15. Найдите координаты вершины параболы
НАЙДИТЕ КООРДИНАТЫ ВЕРШИНЫПАРАБОЛЫ
15
14
17
16
13
у
1
0
.
1
х
16. Сдайте заполненные бланки учителю
СДАЙТЕ ЗАПОЛНЕННЫЕ БЛАНКИУЧИТЕЛЮ
17. 3 этап
3 ЭТАП18. 4 этап
4 ЭТАП19.
Определитесвойства
квадратичной
функции:
1. При каких значениях x
функция положительна?
2. При каких значениях x
функция отрицательна?
3. При каких значениях x
функция равна 0?
4. При каких значениях x
функция убывает?
5. При каких значениях x
функция возрастает?
6. Назовите наименьшее
или наибольшее
значение функции.
у
1
0
1
x
20. 5 этап
5 ЭТАПТЕСТ
21. 6 этап
6 ЭТАПИТОГ
«Исследователи»
22. Замечательное свойство параболы
23. Если вращать параболу вокруг ее оси вращения то получится поверхность, которую называют параболоидом вращения.
ЕСЛИВРАЩАТЬ ПАРАБОЛУ ВОКРУГ ЕЕ ОСИ ВРАЩЕНИЯ ТО
ПОЛУЧИТСЯ
ПОВЕРХНОСТЬ,
НАЗЫВАЮТ ПАРАБОЛОИДОМ ВРАЩЕНИЯ.
КОТОРУЮ
24. Согнем узкую полоску хорошо отполированного металла по дуге параболы: если на эту параболу направить пучок лучей, параллельных
СОГНЕМУЗКУЮ
ПОЛОСКУ
ХОРОШО
ОТПОЛИРОВАННОГО МЕТАЛЛА ПО ДУГЕ ПАРАБОЛЫ:
ЕСЛИ НА ЭТУ ПАРАБОЛУ НАПРАВИТЬ ПУЧОК ЛУЧЕЙ,
ПАРАЛЛЕЛЬНЫХ
ОТРАЖЕНИЯ
ПАРАБОЛЫ
ВСЕ
ОСИСИММЕТРИИ,
ЛУЧИ
СОБЕРУТСЯ
ТО
ПОСЛЕ
В
ФОКУСЕ
25. И наоборот: все лучи, исходящие из источника света, находящегося в фокусе данной параболы, после отражения оказываются
ИНАОБОРОТ: ВСЕ ЛУЧИ, ИСХОДЯЩИЕ ИЗ ИСТОЧНИКА
СВЕТА, НАХОДЯЩЕГОСЯ В ФОКУСЕ ДАННОЙ ПАРАБОЛЫ,
ПОСЛЕ
ОТРАЖЕНИЯ
ПАРАЛЛЕЛЬНО ЕЕ ОСИ
ОКАЗЫВАЮТСЯ
НАПРАВЛЕННЫМИ
26. Эти свойства параболы используются при изготовлении прожекторов, автомобильных фар, карманных фонариков, зеркал, которые имеют
ЭТИСВОЙСТВА
ИЗГОТОВЛЕНИИ
ФАР,
ПАРАБОЛЫ
ИСПОЛЬЗУЮТСЯ
ПРОЖЕКТОРОВ,
КАРМАННЫХ
ФОНАРИКОВ,
ПРИ
АВТОМОБИЛЬНЫХ
ЗЕРКАЛ,
КОТОРЫЕ
ИМЕЮТ ВИД ПАРАБОЛОИДОВ ВРАЩЕНИЯ.
ЗЕРКАЛЬНАЯ АНТЕННА
РЕФЛЕКТОР МИНИНА
27. ПРОЖЕКТОР
28. Автомобильная фара
АВТОМОБИЛЬНАЯ ФАРА29. На Сицилии введена в эксплуатацию солнечная электростанция, производящая электроэнергию даже ночью. Это не бессмыслица, а
НА СИЦИЛИИВВЕДЕНА В ЭКСПЛУАТАЦИЮ СОЛНЕЧНАЯ
ЭЛЕКТРОСТАНЦИЯ,
ДАЖЕ НОЧЬЮ.
ЭТО
ПРОИЗВОДЯЩАЯ
ЭЛЕКТРОЭНЕРГИЮ
НЕ БЕССМЫСЛИЦА, А РЕЗУЛЬТАТ
СОЮЗА МЕЖДУ ДРЕВНИМ ПРИНЦИПОМ И СОВРЕМЕННЫМИ
ТЕХНОЛОГИЯМИ.
30. Реализовать ее первым попытался ученый Архимед в третьем веке до нашей эры, когда для защиты своего родного города Сиракузы от
РЕАЛИЗОВАТЬЕЕ ПЕРВЫМ ПОПЫТАЛСЯ УЧЕНЫЙ
АРХИМЕД
В ТРЕТЬЕМ ВЕКЕ ДО НАШЕЙ ЭРЫ, КОГДА ДЛЯ ЗАЩИТЫ
СВОЕГО
РИМЛЯН,
РОДНОГО
ОН
ГОРОДА
СИРАКУЗЫ
СКОНЦЕНТРИРОВАЛ
ОТ
НАПАДЕНИЯ
СОЛНЕЧНЫЙ
СВЕТ
ПРОТИВ ВРАЖЕСКИХ КОРАБЛЕЙ ДЛЯ ТОГО, ЧТОБЫ СЖЕЧЬ
ИХ.
31. Архимедом, по существу, было изобретено "распределенное" вогнутое зеркало. Составленное из множества обычных зеркал, отражения
АРХИМЕДОМ, ПО СУЩЕСТВУ, БЫЛО ИЗОБРЕТЕНО"РАСПРЕДЕЛЕННОЕ"
ВОГНУТОЕ
ЗЕРКАЛО.
СОСТАВЛЕННОЕ ИЗ МНОЖЕСТВА ОБЫЧНЫХ ЗЕРКАЛ,
ОТРАЖЕНИЯ ОТ КОТОРЫХ БЫЛИ НАПРАВЛЕНЫ В ОДНУ
ТОЧКУ
32. Домашнее задание:
ДОМАШНЕЕ ЗАДАНИЕ:№ 634, № 635, № 637




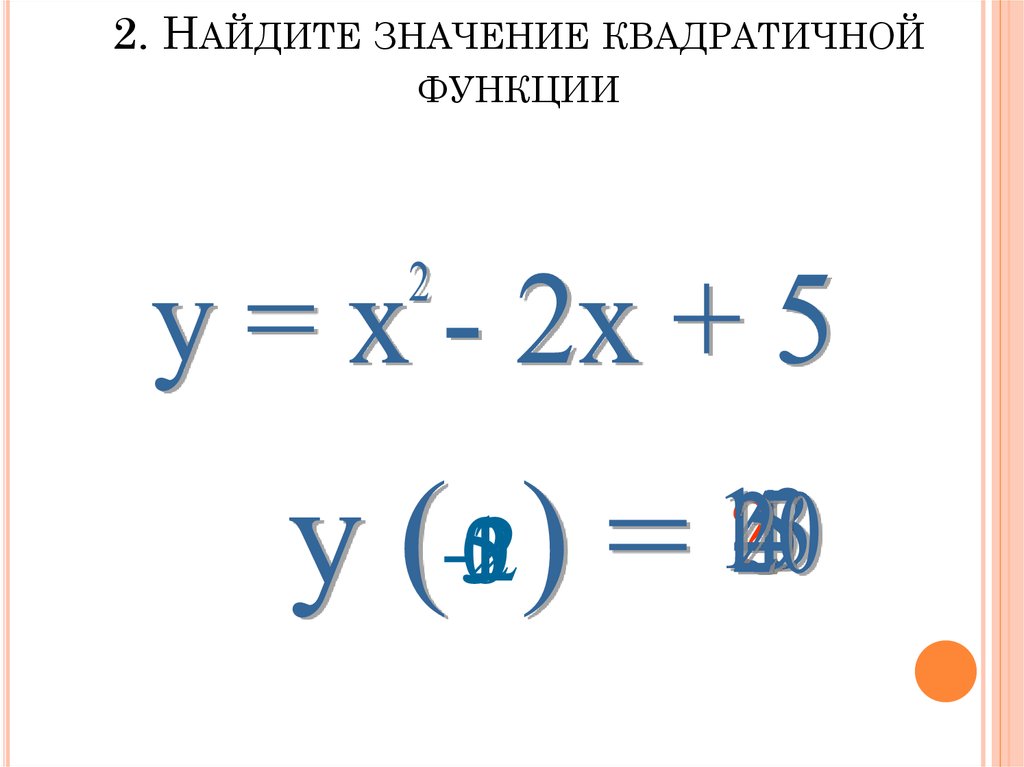

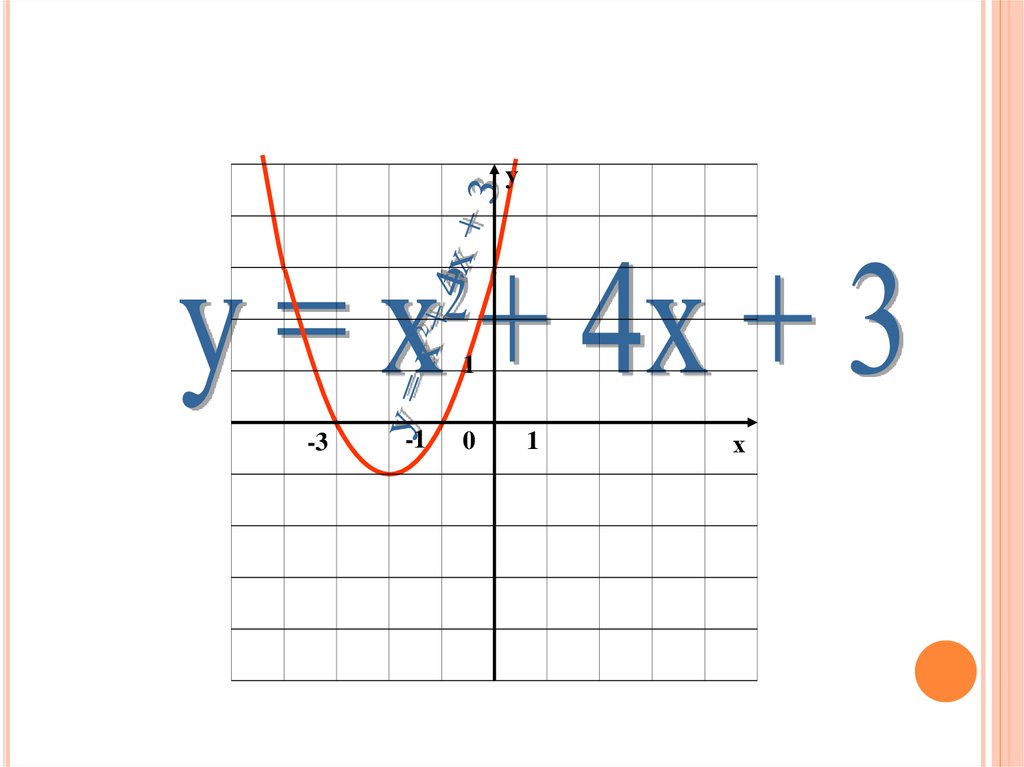





















 mathematics
mathematics








