Взаимное расположение графиков линейных функций

1.

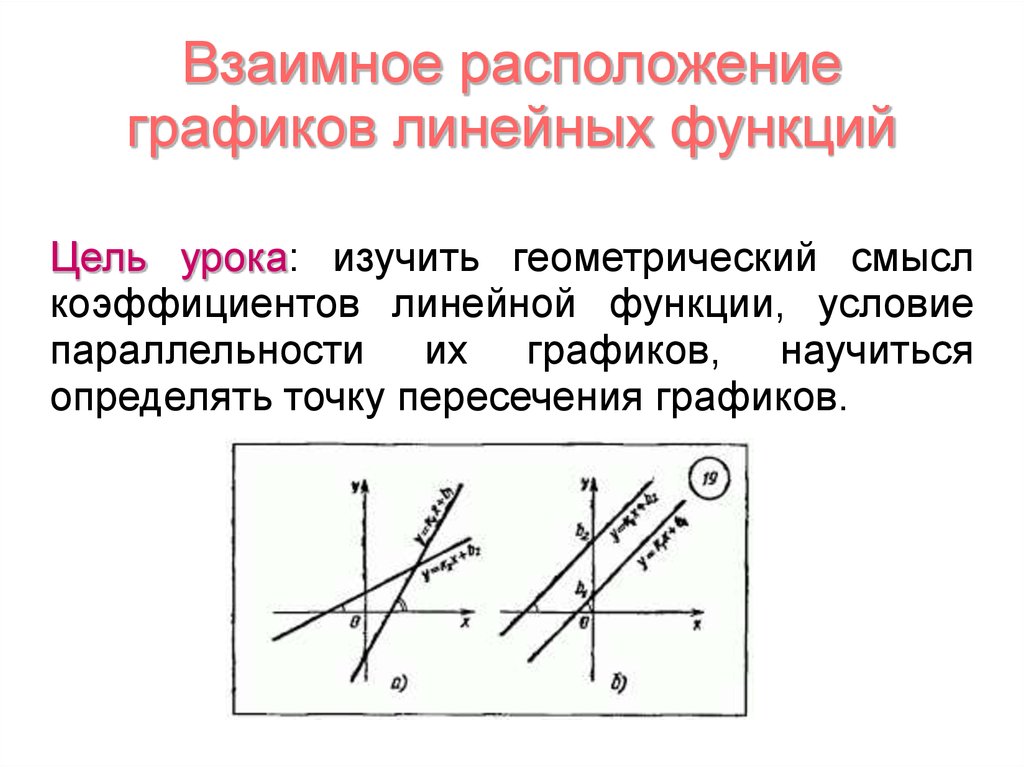
Взаимное расположение
графиков линейных функций
Цель урока: изучить геометрический смысл
коэффициентов линейной функции, условие
параллельности их графиков, научиться
определять точку пересечения графиков.

2.

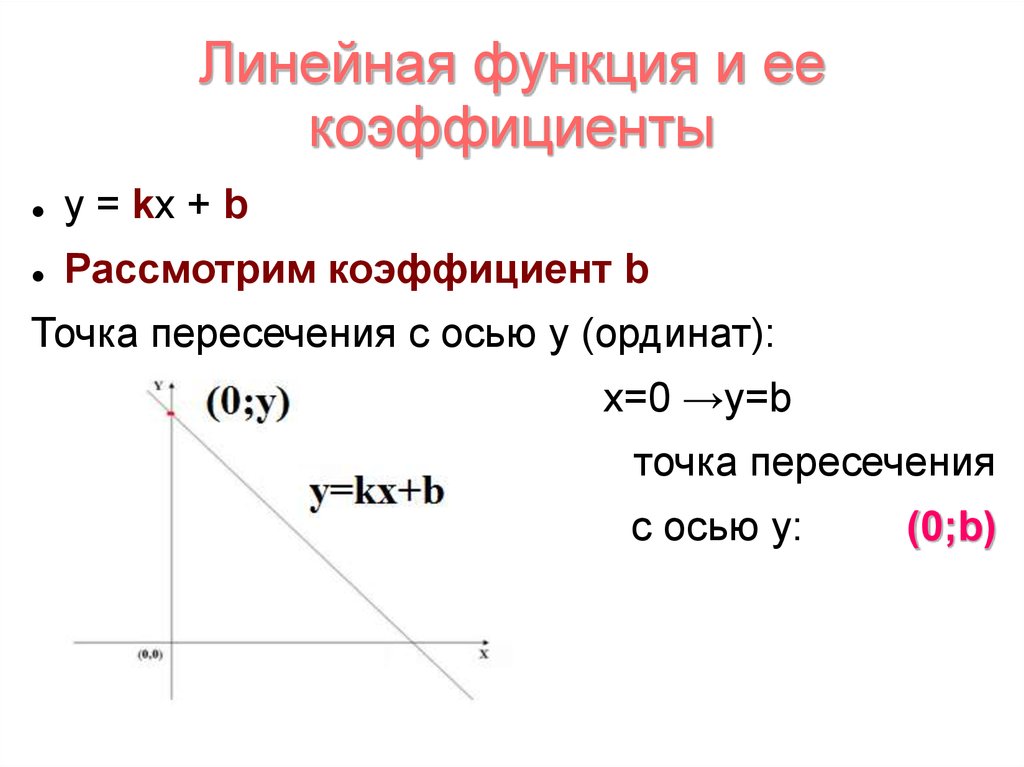
Линейная функция и ее
коэффициенты
y = kx + b
Рассмотрим коэффициент b
Точка пересечения с осью у (ординат):
х=0 →у=b
точка пересечения
с осью у:
(0;b)

3.

Определите точку пересечения
графика функции с осью у:
у=2
у=5х + 19
(0;19)
у=-7х — 24
(0;-24)
(0;2)
(0;0)

4.

Устные упражнения
Приведите пример линейной функции, график
которой пересекает ось ординат
В точке А(0;3)
В точке B(0;-2)
В точке O(0;0)
ВЫВОД: коэффициент b показывает точку
пересечения графика линейной функции с
осью у.

5.

Угловой коэффициент прямой
у=kх+b

6.

Угловой коэффициент прямой

7.

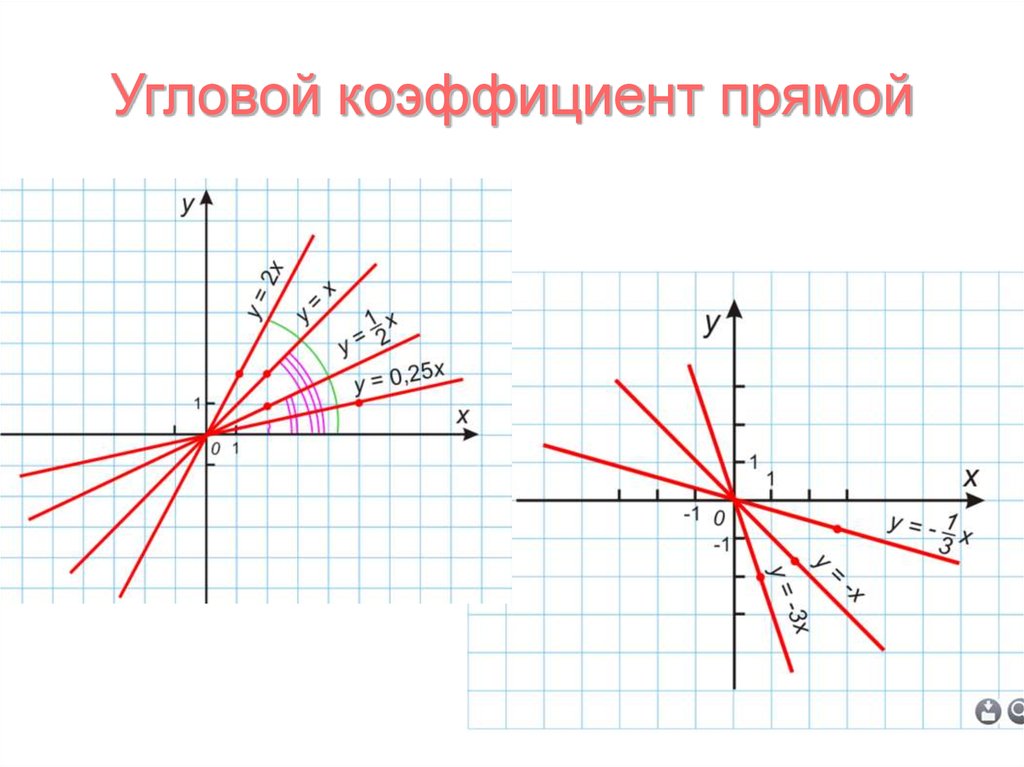
Коэффициент k — угловой
коэффициент
k>0 — угол наклона прямой у=kx+b к оси х
острый;
k<0 — угол наклона прямой у=kx+b к оси х
тупой.

8.

Взаимное расположение
графиков линейных функций
Прямые пересекаются: k1≠k2
у=k1x+b1
y=k2x+b2

9.

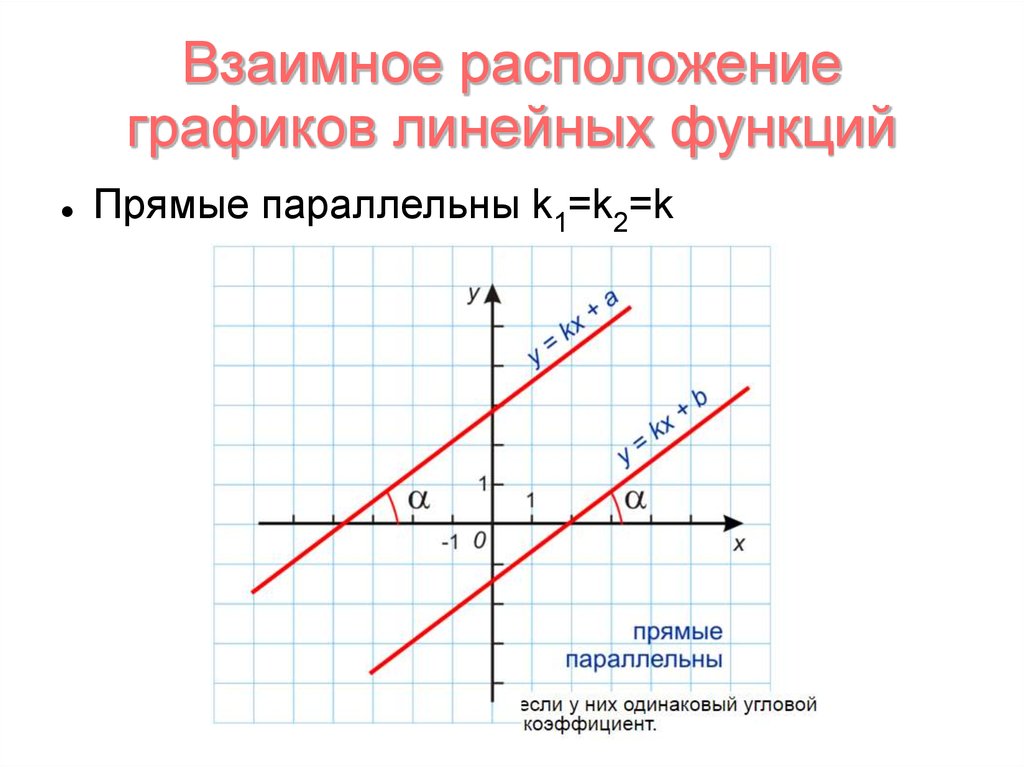
Взаимное расположение
графиков линейных функций
Прямые параллельны k1=k2=k

10.

Устные упражнения:
Каким является угол наклона к оси х прямой,
заданной формулой:
у=6х + 2
у=-4х + 5
у=0,5х
у=4
Каково взаимное расположение прямых:
у=2х + 5 и у =-2х + 5
у=2х и у= 2х + 1

11.

Пример 1 учебника:
Найдите координаты точки пересечения
графиков функций у = -3х + 1 и у = х — 3
М (х0;у0) — искомая точка
у = -3х + 1
у=х—3
у0 = -3х0 + 1
у0 = х 0 — 3
-3х0 + 1 = х0 — 3
-4х0 = -4
х0=1
у0=-3+1=-2 Ответ: (1;-2)

12.

Работа в классе:
№1081 а, 1082, 1083, 1084 а,в, 1086 а,в,
1088 а,в,д.
Домашнее задание:
п.39, № 1081б, 1084 б,г, 1086 б,г, 1088 б,г,е,
1092.

13.

Выводы
• Функция вида y = kx + b, где k и b - действительные числа,
называется линейной функцией. Графиком линейной функции
является прямая.
• Функцию вида y = kx называют прямой пропорциональностью,
и её график проходит через начало координат.
• График функции y = b параллелен оси абсцисс и проходит через
точку с координатами (0; b).
• Коэффициент k называют угловым коэффициентом. От него
зависит угол наклона прямой к оси ОX.
• Если у двух различных прямых равны угловые коэффициенты,
то графики этих функций будут параллельны.