Similar presentations:
Квадратные уравнения
1. АЛГЕБРА, 8 класс Тема урока: «Квадратные уравнения»
МКОУ Большеясырская ООШАЛГЕБРА, 8 КЛАСС
ТЕМА УРОКА:
«КВАДРАТНЫЕ УРАВНЕНИЯ»
Автор: Ананьева О.В..
2.
ОПРЕДЕЛЕНИЕ:Квадрат ным уравнением называется
уравнение вида ах2 + вх +с = 0,
где х –переменная,
а, в и с некоторые числа,
причем а 0.
3.
КВАДРАТНЫЕ УРАВНЕНИЯПОЛНЫЕ
КВАДРАТНЫЕ УРАВНЕНИЯ
а ≠ 0, в ≠ 0,
с ≠ 0
НЕПОЛНЫЕ
КВАДРАТНЫЕ УРАВНЕНИЯ
а ≠ 0, в = 0, с = 0
2х2+5х-7=0
3х2-2х=0
6х+х2-3=0
2х+х2=0
Х2-8х-7=0
125+5х2=0
25-10х+х2=0
49х2-81=0
4.
Определите коэффициентыквадратного уравнения:
а) 6х2 – х + 4 = 0
а = 6, в = -1, с = 4;
б) 12х - х2 + 7 = 0
а = -1, в = 12, с = 7;
в) 8 + 5х2 = 0
а = 5, в = 0, с = 8;
г) х – 6х2 = 0
а = -6, в =1, с = 0;
д) - х + х2 = 15
а = 1, в =-1, с = -15.
5.
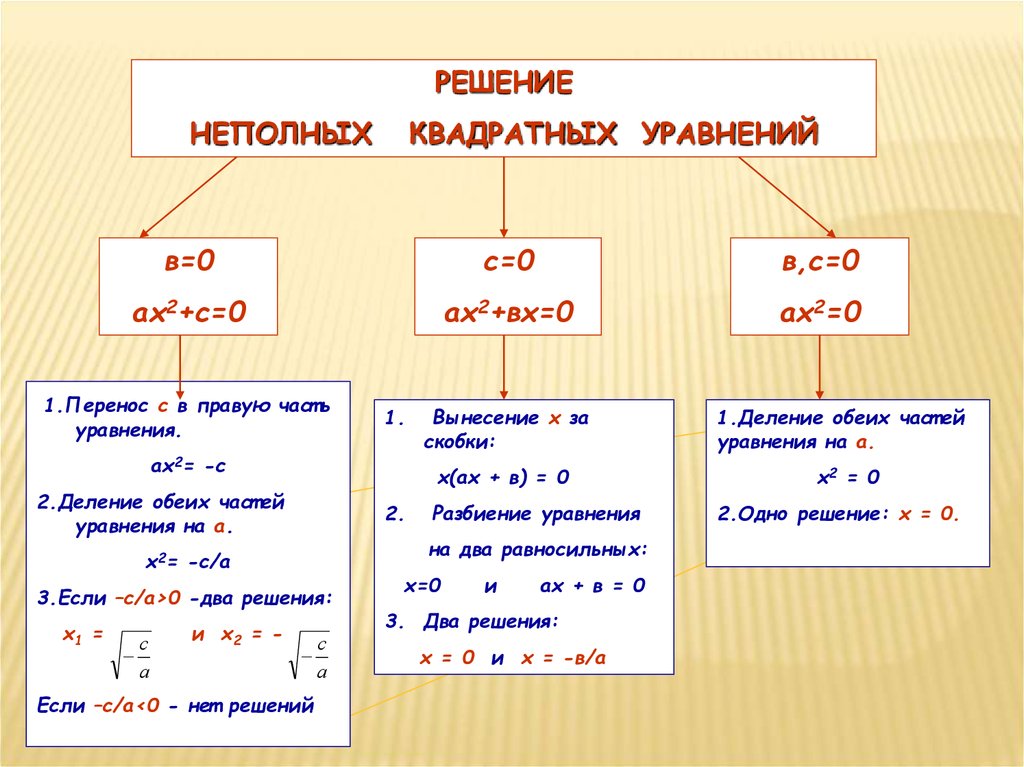
РЕШЕНИЕНЕПОЛНЫХ
КВАДРАТНЫХ УРАВНЕНИЙ
в=0
с=0
в,с=0
ах2+с=0
ах2+вх=0
ах2=0
1.Перенос с в правую част ь
уравнения.
1.
ах2= -с
х(ах + в) = 0
2.Деление обеих част ей
уравнения на а.
2.
3.Если –с/а>0 -два решения:
с
а
и х2 = -
Разбиение уравнения
на два равносильных:
х2= -с/а
х1 =
Вынесение х за
скобки:
Если –с/а<0 - нет решений
с
а
х=0
и
ах + в = 0
3. Два решения:
х = 0 и х = -в/а
1.Деление обеих част ей
уравнения на а.
х2 = 0
2.Одно решение: х = 0.
6.
РЕШИ САМОСТОЯТЕЛЬНО УРАВНЕНИЯ :1 вариант :
а) 1 х 2 8 0
3
27
б) ( х + 2)2 + ( х -3)2 = 13
2 вариант :
а) 2х + х2= 0
б) 49х2 – 81 = 0
3 вариант :
а) 3х2 – 2х = 0
б) 125 + 5х2 = 0
7.
Способы решенияполных квадратных уравнений
1. Выделение квадрата двучлена.
1. Формула: D = b2- 4ac, x1,2=
2. График.
3. Теорема Виета.
b D
2a
8.
РЕШИ УРАВНЕНИЯспособом выделения квадрат а
двучлена :
1 вариант :
- х + 3х2 – 70 =0
2 вариант :
2х2 -9х + 10 = 0
3 вариант :
х2 – 8х -9 = 0
9.
РЕШИ УРАВНЕНИЯс помощью формулы :
1 вариант :
а) -7х + 5х2 + 1 =0
б) (х – 1)(х + 1) = 2 (5х – 10,5)
2 вариант :
а) 2х2 + 5х -7 = 0
б) –х2 = 5х - 14
3 вариант :
а) х2 – 8х + 7 = 0
б) 6х – 9 = х2
10.
РЕШИ УРАВНЕНИЯграфически :
1 вариант:
1/3х2 -х = - 2/3
2 вариант:
а) х2 + 1,5х = 2,5
3 вариант:
а) 6х + х2– 3 =0
11.
Ист орические сведения:Квадрат ные уравнения впервые вст речают ся в
работ е индийского мат емат ика и аст ронома
Ариабхатты.
Другой индийский ученый Брахмагупт а (VII в)
изложил общее правило решения квадрат ных
уравнений, кот орое практ ически совпадает с
современным.
В Древней Индии были распрост ранены
публичные соревнования в решении т рудных
задач.











 mathematics
mathematics








