Решение тригонометрических неравенств

1.

2.

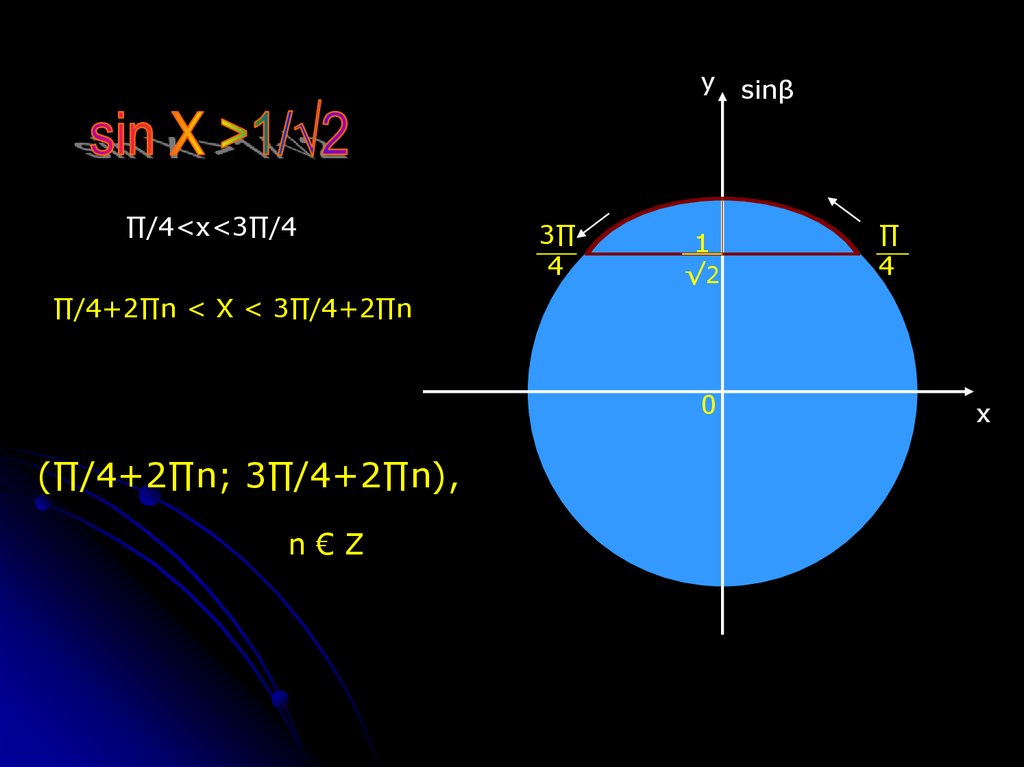
y sinβ
∏/4<x<3∏/4
3∏
4
1
√2
∏
4
∏/4+2∏n < X < 3∏/4+2∏n
0
(∏/4+2∏n; 3∏/4+2∏n),
n€Ζ
x

3.

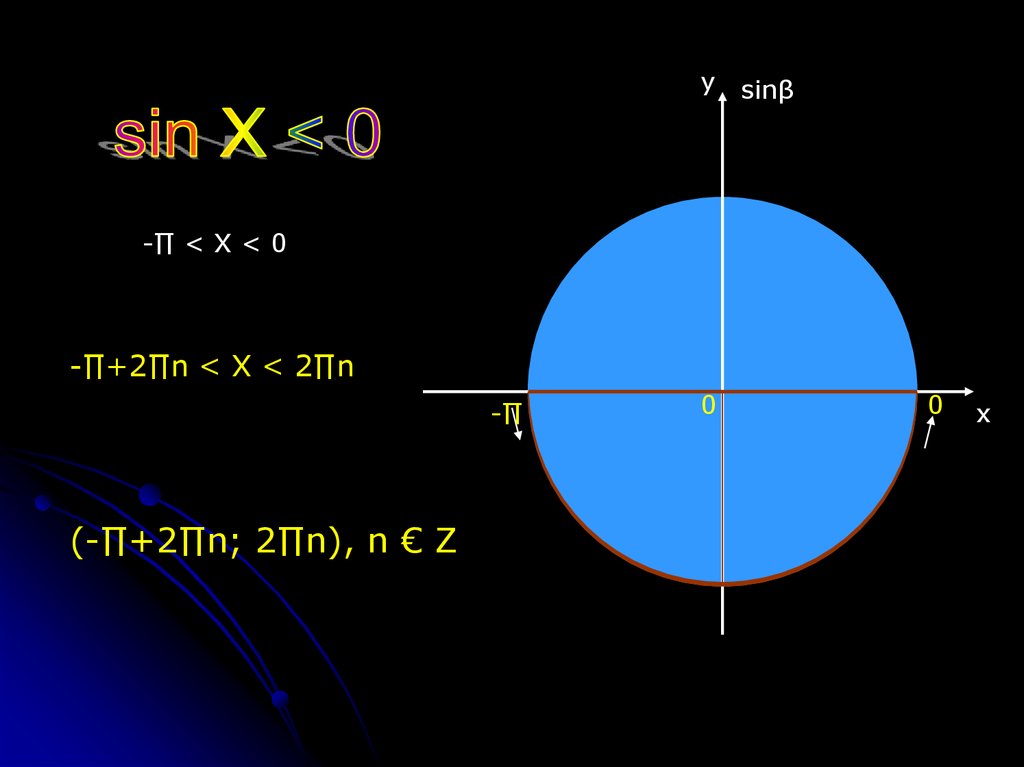
y sinβ
-∏ < X < 0
-∏+2∏n < X < 2∏n
-∏
(-∏+2∏n; 2∏n), n € Ζ
0
0
x

4.

y
3∏/4<x<5∏/4
3∏
4
3∏/4+2∏n < X < 5∏/4+2∏n
1
√2
(3∏/4+2∏n; 5∏/4+2∏n),
n€Ζ
5∏
4
cos β
0
x

5.

y
∏
2
-∏/2 < X < ∏/2
cos β
0
-∏/2+2∏n < X < ∏/2+2∏n
(-∏/2+2∏n;∏/2+2∏n), n € Ζ
∏
2
x

6.

y
∏/6≤x<∏/2
∏/6+∏n ≤ x < ∏/2+∏n
tg β
∏
2
∏ 1
6 √3
[∏/6+∏n; ∏/2+∏n),n€ Ζ
x

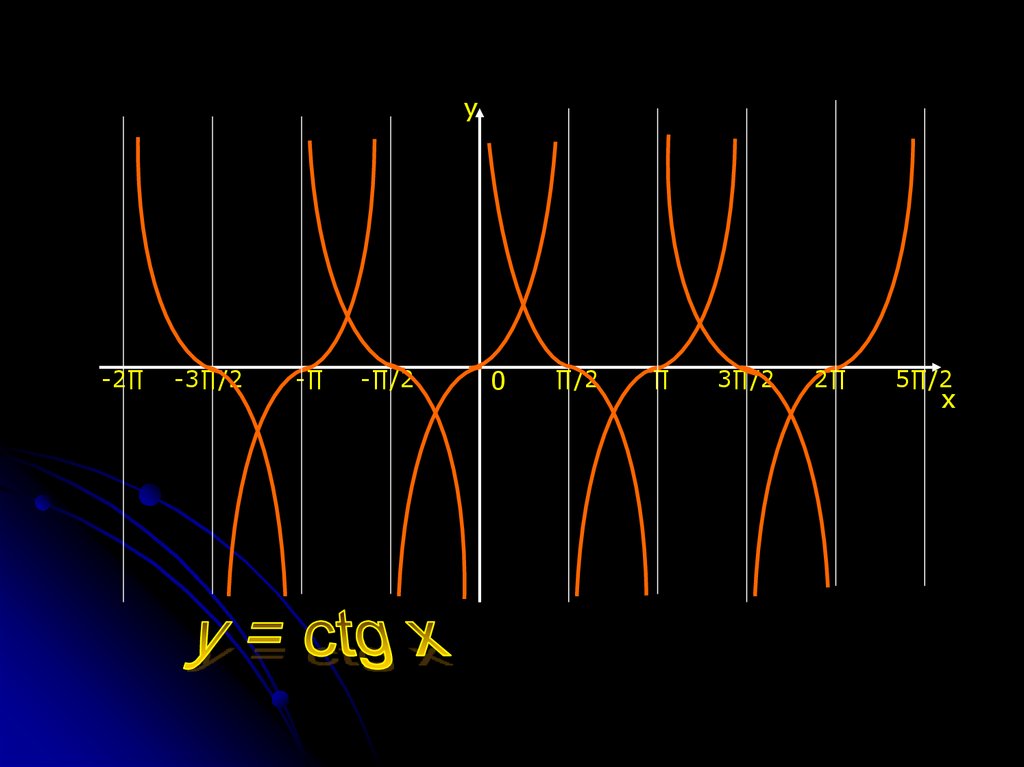
7.

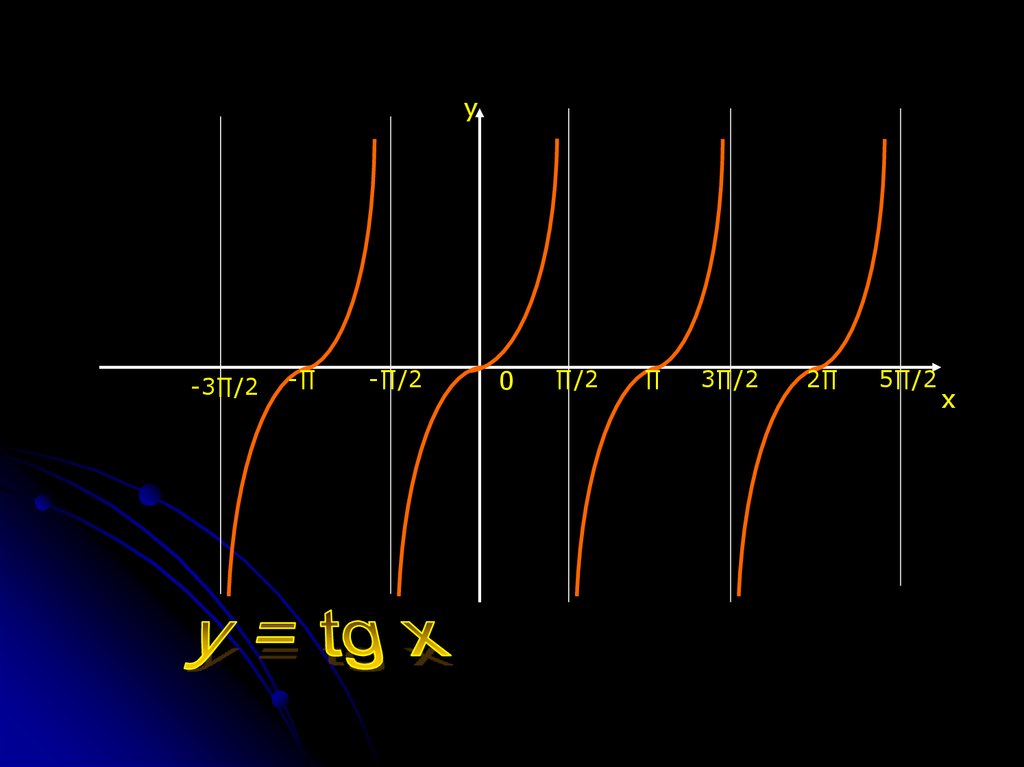
y
tg β
x
-∏/2 < x ≤ -∏/4
-∏/2+∏n < x ≤ -∏/4+∏n
(-∏/2+∏n;-∏/4+∏n],n€ Ζ
∏
2
∏
4
-1

8.

9.

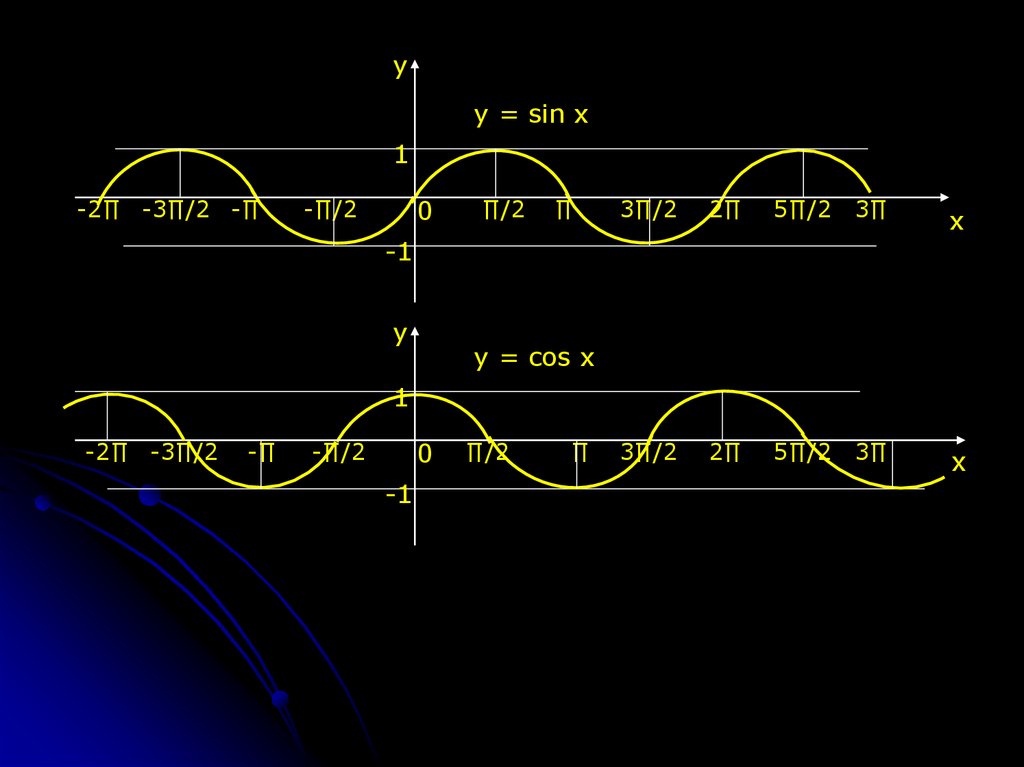
y
y = sin x
1
-2∏ -3∏/2 -∏
0
-∏/2
∏/2
∏
3∏/2
2∏
5∏/2
3∏
x
3∏/2
2∏
5∏/2
3∏
x
-1
y
y = cos x
1
-2∏ -3∏/2
-∏
0
-∏/2
-1
∏/2
∏

10.

у
-3∏/2
-∏
-∏/2
0
∏/2
∏
3∏/2
2∏
5∏/2
х

11.

у
-2∏
-3∏/2
-∏
-∏/2
0
∏/2
∏
3∏/2
2∏
5∏/2
х

12.

13.

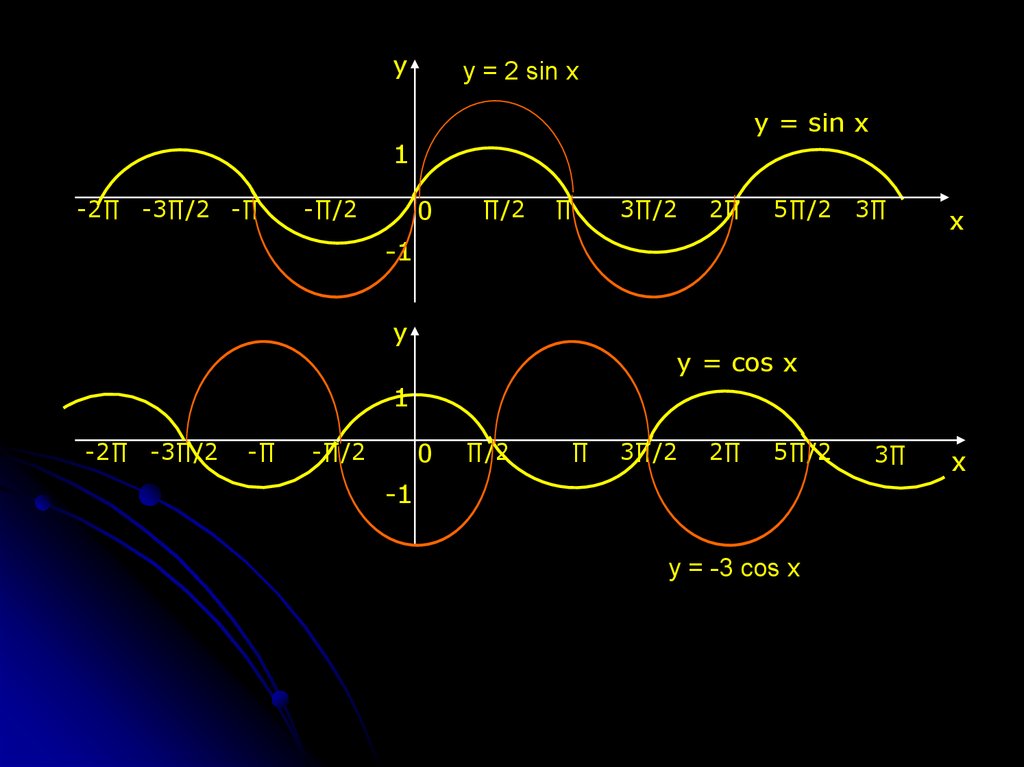
y
y = 2 sin x
y = sin x
1
-2∏ -3∏/2 -∏
0
-∏/2
∏/2
∏
3∏/2
2∏
5∏/2
3∏
-1
y
x
y = cos x
1
-2∏ -3∏/2
-∏
0
-∏/2
∏/2
∏
3∏/2
2∏
5∏/2
-1
y = -3 cos x
3∏
x

14.

y
y = sin 2x
y = sin x
1
-2∏ -3∏/2 -∏
0
-∏/2
∏/2
∏
3∏/2
2∏
5∏/2
3∏
x
3∏
x
-1
y
y = cos x
1
-2∏ -3∏/2
-∏
0
-∏/2
-1
∏/2
∏
3∏/2
2∏
5∏/2
y = cos ½ x