Решение систем уравнений второй степени

1.

Математику уже затем учить надо,
что она ум в порядок приводит.
М.В.Ломоносов
Полет – это математика
В.Чкалов
Если вы хотите участвовать в
большой жизни, то наполняйте свою
голову математикой, пока есть к
тому возможность. Она окажет вам
потом огромную помощь во всей вашей
работе.
М.И.Калинин

2.

3. Цели урока:

1.
Продолжить формирование навыков
решения систем уравнений второй степени
2.
Повторить теоретический материал по данной
теме
3.
Продолжить формирование навыков
сознательного выбора способа решения системы
4.
Развивать потребность в нахождении
рациональных способов решения
5.
Воспитывать такие качества личности, как
познавательная активность, самостоятельность.

4.

Три пути ведут к знанию:
Путь размышлений – самый благородный,
Путь подражания – самый легкий
И путь опыта – самый горький…
Конфуций

5. Мое настроение

6. Математический диктант

Что называется решением системы с
двумя переменными?
Какие системы уравнений
называются равносильными?

7. Математический диктант

№1.
Х 2 У 2 100;
3 Х 2У 2 0.
Является ли решением системы:
(6;-8)
(8;-6)
№2. Выразите:
А) у через х
х2-у-5=0
Б) х через у
5х+ у2=14
В) х через у и у через х:
2х-у=20
Да
Нет
у=х2- 5
х=(14 -у2): 5
у=2х - 20
х=10 + 0,5у

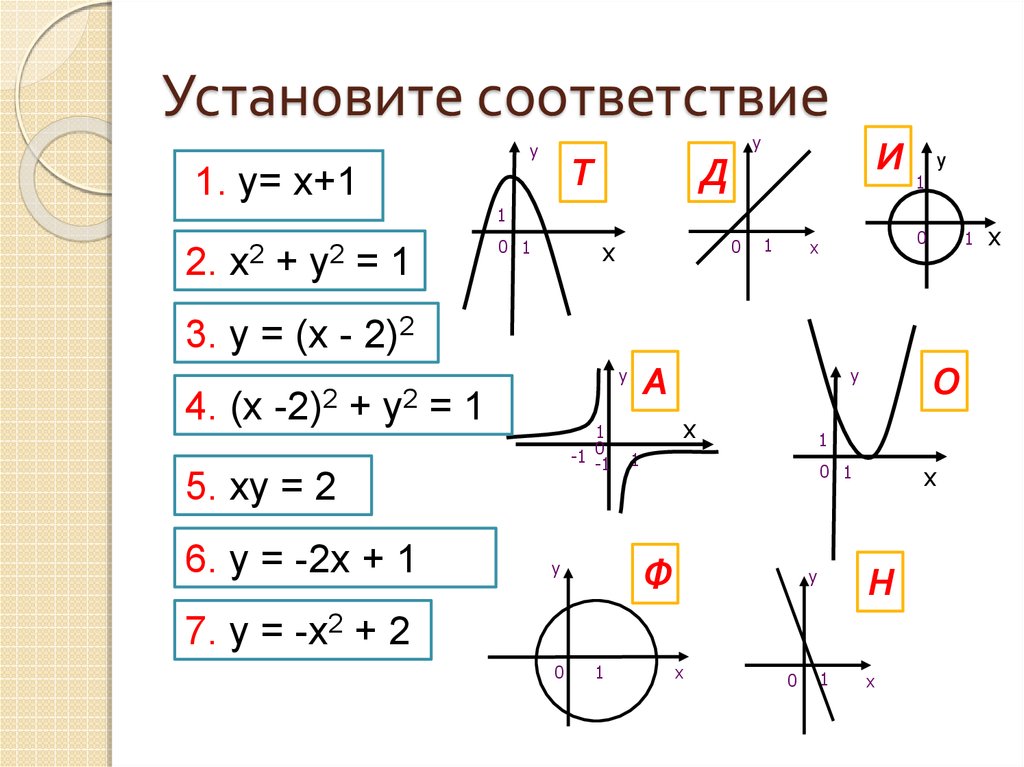
8. Установите соответствие

y
y
1. у= х+1
Т
И
Д
у
1
1
2.
х2
+
у2
0 1
=1
0
х
1
0
x
1
3. у = (х - 2)2
4. (х
-2)2
+
у2
=1
1
0
-1 -1
5. ху = 2
6. у = -2х + 1
А
y
х
1
1
0 1
Ф
y
О
y
х
Н
y
7. у = -х2 + 2
0
1
x
0
1
x
х

9. Домашнее задание

«Прах Диофанта гробница покоит; дивись ей и камень
Мудрым искусством его скажет усопшего век.
Волей богов шестую часть жизни он прожил ребенком.
И половину шестой встретил с пушком на щеках.
Только минула седьмая, с подругою он обручился.
С нею пять лет проведя, сына дождался мудрец;
Только полжизни отцовской возлюбленный сын его прожил.
Отнят он был у отца ранней могилой своей.
Дважды два года родитель оплакивал тяжкое горе,
Тут и увидел предел жизни печальной своей»

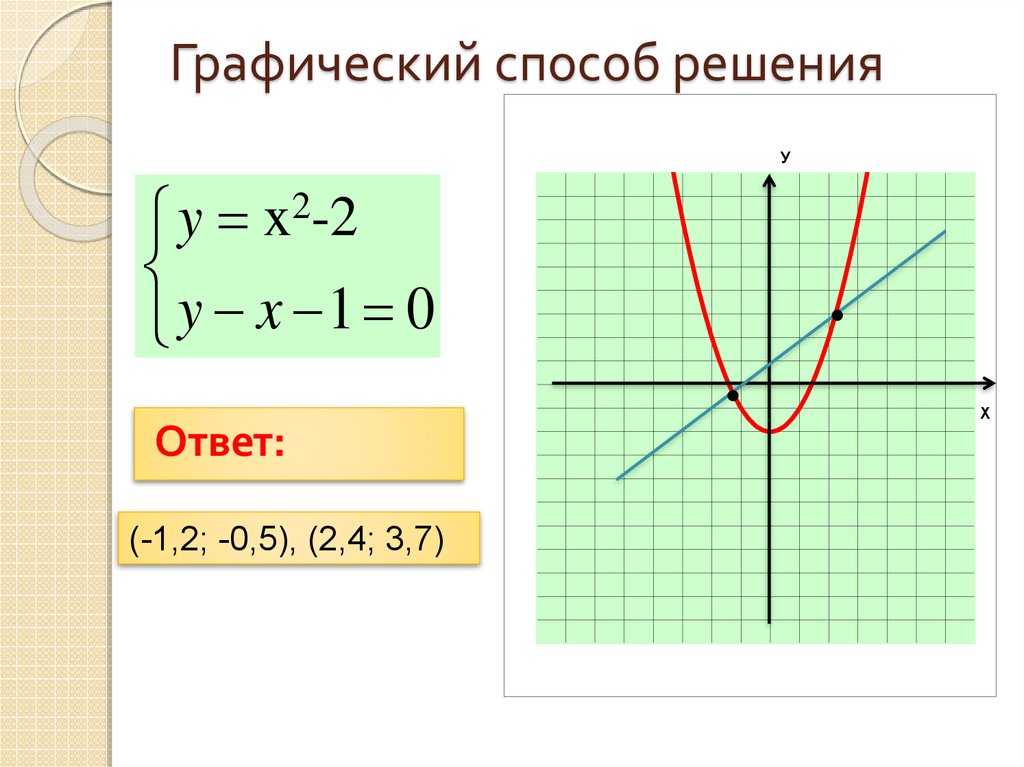
10. Графический способ решения

У
2-2
x
y
y x 1 0
Ответ:
(-1,2; -0,5), (2,4; 3,7)
Х

11. Графический способ решения

ху 6
Ответ
14
У
13
12
11
10
9
8
7
6
5
4
3
2
1
0
-11-10 -9 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9 10 11
-2
-3
-4
-5
-6
-7
-8
-9
-10
-11
-12
-13
-14

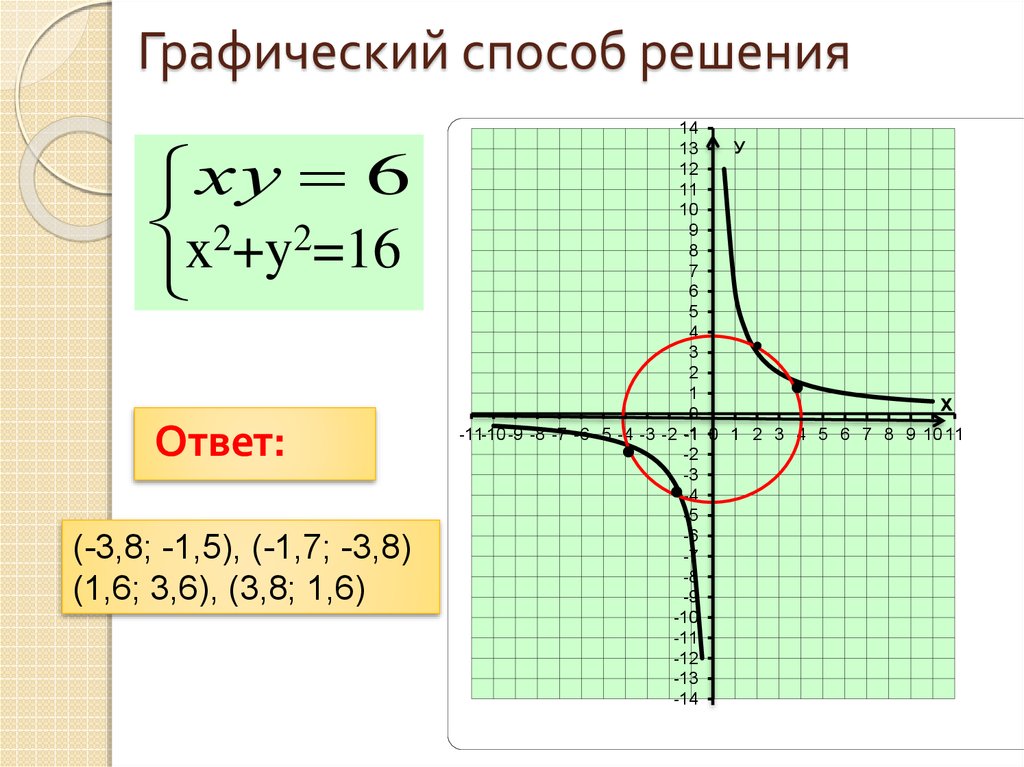
12. Графический способ решения

ху 6
x2+y2=16
Ответ:
(-3,8; -1,5), (-1,7; -3,8)
(1,6; 3,6), (3,8; 1,6)
14
У
13
12
11
10
9
8
7
6
5
4
3
2
1
0
-11-10 -9 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9 10 11
-2
-3
-4
-5
-6
-7
-8
-9
-10
-11
-12
-13
-14

13. Знание – самое превосходное из владений. Все стремятся к нему, само же оно не приходит Абу-р-Райхан ал-Бируни

14. Решите систему

х у 1
х у 1
2
Ответ
Решение 1
Решение 2

15. Решите систему

х 2 у 1
х у 1
2
Ответ
Решение 1
Решение 2

16. Решите систему

( х 15)( у 11) 0
2
2
( х 15) ( у 11) 0
Решение
Ответ

17. Решите систему

х у х у 12
ху 15
2
2
Решение
Ответ

18. Итог урока

1. Назовите решение системы:
( х 4)( у 15) 0
2
2
( х 4) ( у 15) 0
2. Являются ли равносильными системы?
х у 5
ху 2
2
2
( х у ) 9
ху 2
2

19. Итак, сегодня мы с вами

Закрепили знания, умения и навыки по
теме «Решение систем уравнений
второй степени»
Познакомились с великим ученым
Диофантом
Побывали в роли исследователей
Эпиграф

20. Домашнее задание

Задача из «Арифметики» Диофанта:
Найти два числа, зная, что их сумма
равна 20, а сумма их квадратов – 208.
х у 20
2
2
х у 208

21. Домашнее задание

ху 2
2
2
х у 5
( х 11)( у 8) 0
2
2
(
х
11
)
(
у
8
)
0
ху 15
2
2
х у х у 42

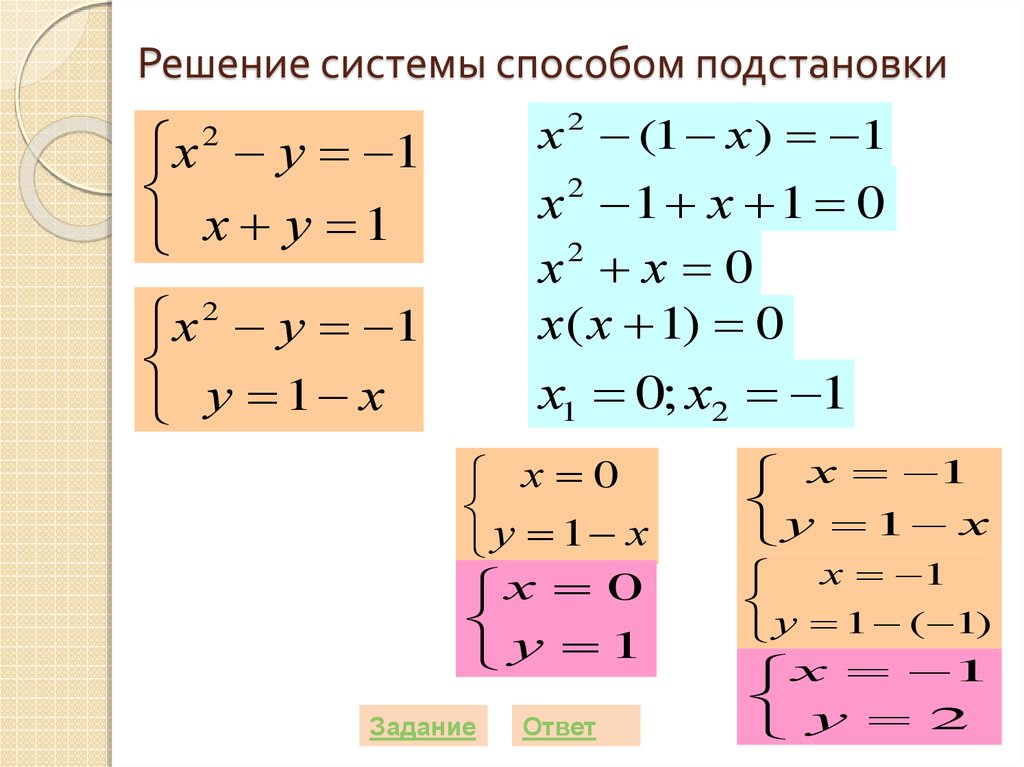
22. Решение системы способом подстановки

х 2 (1 х) 1
х у 1
х у 1
2
х 1 х 1 0
х2 х 0
х( х 1) 0
х1 0; х2 1
2
х 2 у 1
у 1 х
х 0
у 1 х
х 0
у 1
Задание
Ответ
х 1
у 1 х
х 1
у 1 ( 1)
х 1
у 2

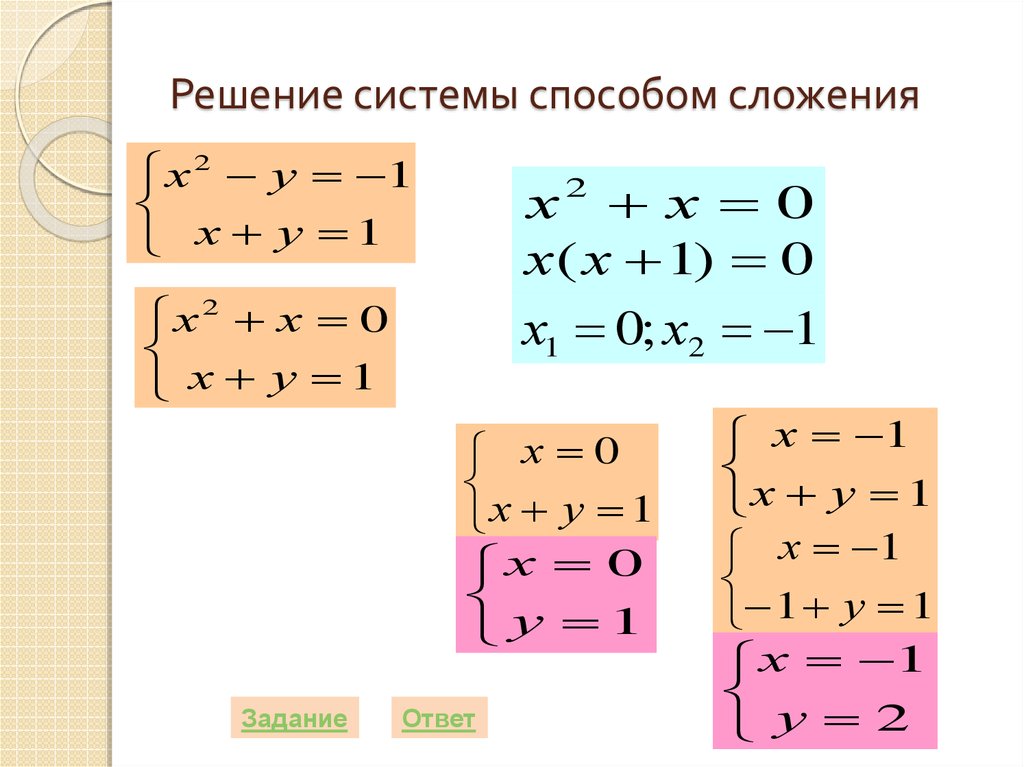
23. Решение системы способом сложения

х 2 у 1
х у 1
х х 0
х( х 1) 0
х1 0; х2 1
2
х2 х 0
х у 1
х 0
х у 1
х 0
у 1
Задание
Ответ
х 1
х у 1
х 1
1 у 1
х 1
у 2

24. Решите систему

х 2 у 1
х у 1
Задание
Решение 1
Решение 2

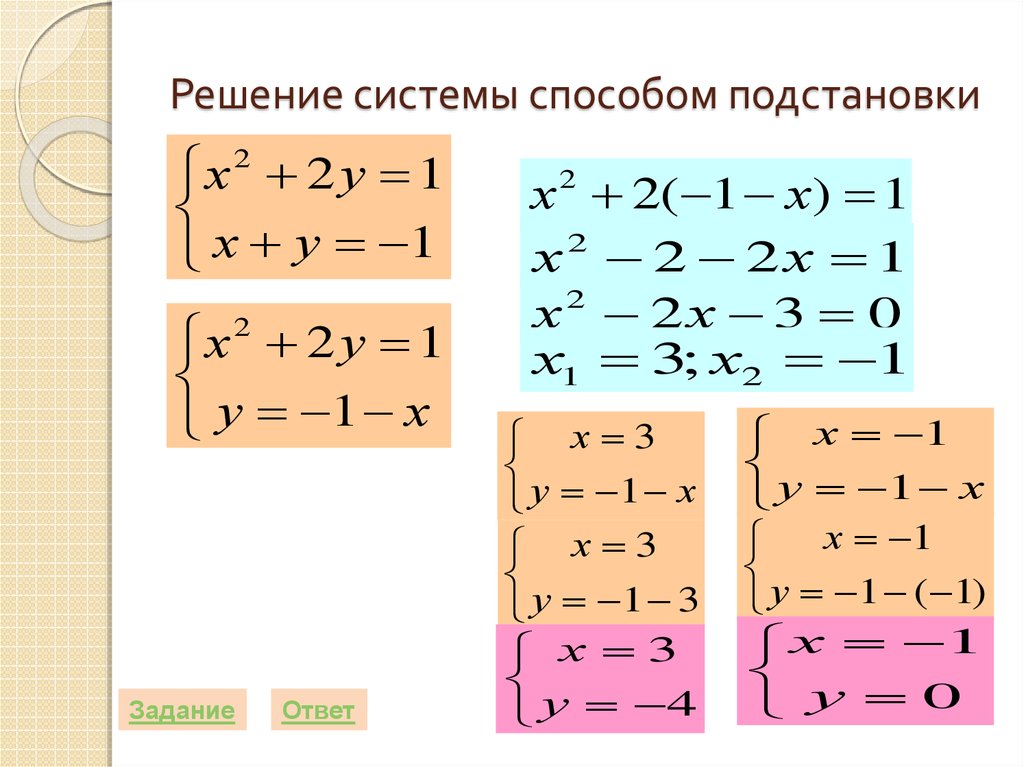
25. Решение системы способом подстановки

х2 2 у 1
х у 1
х2 2 у 1
у 1 х
Задание
Ответ
х 2 2( 1 х) 1
х2 2 2х 1
х2 2х 3 0
х1 3; х2 1
х 3
у 1 х
х 3
у 1 3
х 3
у 4
х 1
у 1 х
х 1
у 1 ( 1)
х 1
у 0

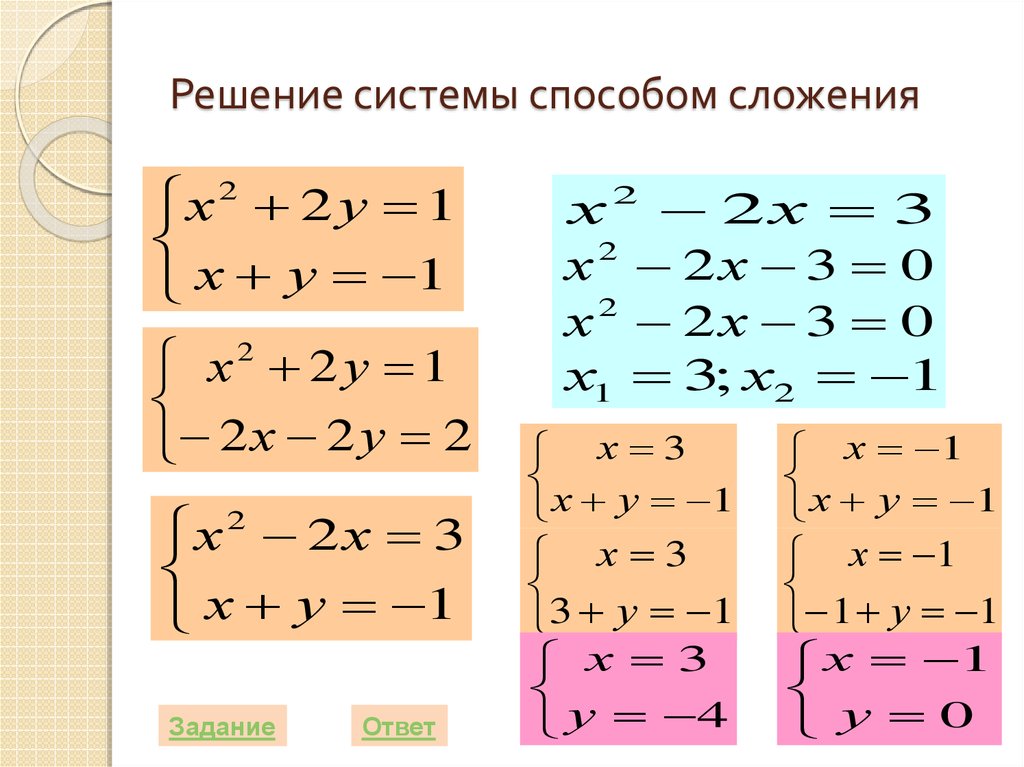
26. Решение системы способом сложения

х2 2 у 1
х у 1
х2 2 у 1
2 х 2 у 2
х 2х 3
х у 1
2
Задание
Ответ
х
2
х
2
х
х1
2х 3
2х 3 0
2х 3 0
3; х2 1
2
х 3
х у 1
х 1
х у 1
х 3
3 у 1
х 3
у 4
х 1
1 у 1
х 1
у 0

27. Решите систему

х2 2 у 1
х у 1
Задание
Решение 1
Решение 2