Similar presentations:
Решение систем уравнений второй степени
1.
Урок по теме:«Решение систем
уравнений второй
степени»
9 класс
FokinaLida.75@mail.ru
2.
Цели урока:• Что называется решением системы уравнений с
двумя переменными;
• Как можно найти решение системы;
• Назвать методы решения систем уравнений;
• Вспомнить алгоритмы;
• Применить эти методы на практике;
• Проверить себя;
• Узнать новое
FokinaLida.75@mail.ru
3.
Тест1. Что называется решением системы уравнений
с двумя переменными?
а) пара значений переменных, обращающая каждое
уравнение системы в верное равенство;
б) значение переменной у;
в) значение переменной х;
г) пары координат точек пересечения графиков
уравнений
FokinaLida.75@mail.ru
4.
2. Какая пара чисел является решениемданной системы уравнений х у 3,
2
2
х
у
3
а) ( 6; 3 );
б) (-3; -6);
в) (2; -1);
г) ( 3; 0 );
FokinaLida.75@mail.ru
5.
3. Какие существуют способы решения системуравнений с двумя переменными?
а) графический способ;
б) способ сложения;
в) иллюстративный способ;
г) способ подстановки
д) способ замены
FokinaLida.75@mail.ru
6.
4. Составьте алгоритм решения систем уравнений сдвумя переменными способом подстановки
а) решить получившееся уравнение с одной
переменной;
б) выразить из какого-нибудь уравнения одну
переменную через другую;
в) найти соответствующее значение второй
переменной ;
г) подставить полученное выражение во второе
уравнение
FokinaLida.75@mail.ru
7.
5. Что называется графиком уравнения с двумяпеременными?
а) множество точек координатной плоскости,
координаты которых обращают уравнение в
верное равенство;
б) координаты точек;
в) пара координат любой точки;
г) множество точек координатной плоскости
FokinaLida.75@mail.ru
8.
6. Составьте алгоритм решения системы уравненийграфическим способом
а) найти точки пересечения графиков уравнений:
б) построить в одной системе координат графики уравнений;
в) записать ответ:
г) определить координаты точек пресечения графиков.
FokinaLida.75@mail.ru
9.
7. Изобразив схематически графики, выясните,имеет ли решения система уравнений и если
имеет, то сколько? х 2 у 2 16,
у х 2
а) одно решение;
б) два решения;
в) три решения;
г) четыре решения
д) нет решений
FokinaLida.75@mail.ru
10.
8. Выберите правильное соответствиеуравнений и графиков уравнений
1.
ху 4;
2.
у х 3;
3.
х у 9;
4.
5.
FokinaLida.75@mail.ru
2
2
8
у ;
х
2
у х 2
а) гипербола (1 и 3 четверти)
б) окружность
в) прямая
г) парабола (ветви направлены
вверх)
д) гипербола (2 и 4 четверти)
е) парабола (ветви направлены
вниз)
11.
9. С помощью графика, изображенного на рисунке,определите, сколько решений имеет система
уравнений?
у
а) одно решение
б) два решения
в) три решения
г) четыре решения
д) нет решений
FokinaLida.75@mail.ru
0
х
12.
10. Установите соответствие между графикамифункций и формулами, которые их задают
А)
1
0
1)
FokinaLida.75@mail.ru
у
Б)
у
10 1
х
2
2)
у ( х 1)
2
3)
у
1
1
1
у ( х 1)
В)
х
2
у
х
0 1
4)
у х 1
х
13.
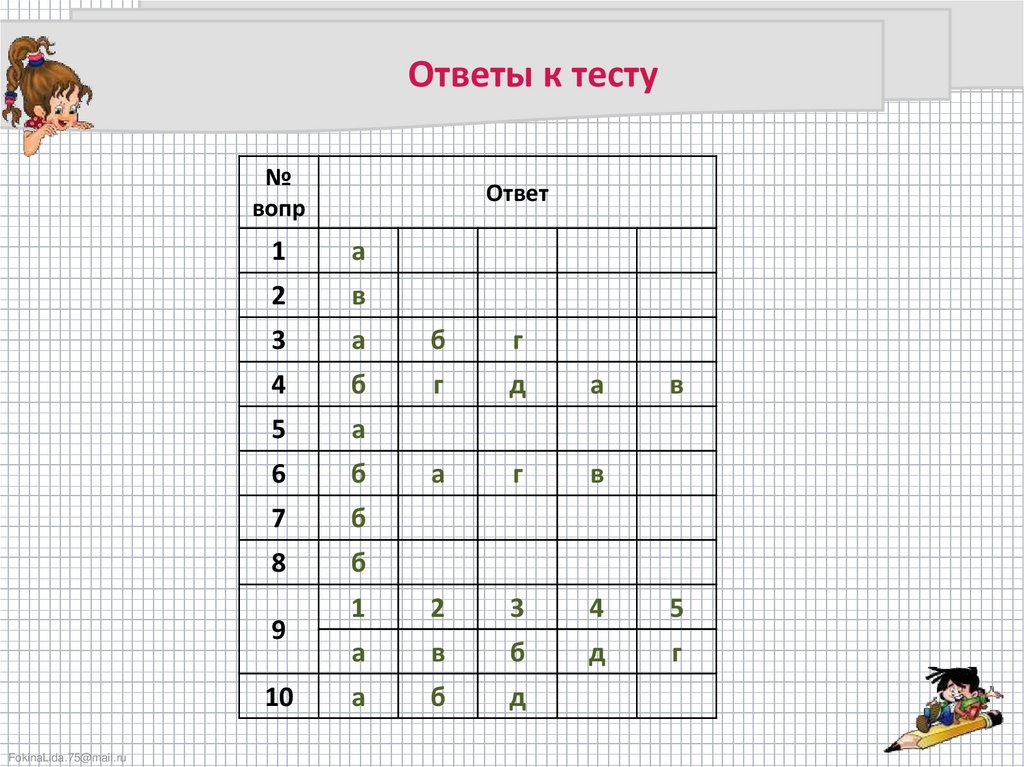
Ответы к тесту№
вопр
1
а
2
в
3
а
б
г
4
б
г
д
а
5
а
6
б
а
г
в
7
б
8
б
1
2
3
4
5
а
в
б
д
г
а
б
д
9
10
FokinaLida.75@mail.ru
Ответ
в
14.
Системы уравненийГрафический способ
Метод
подстановки
FokinaLida.75@mail.ru
Аналитический способ
Метод
сложения
Метод
замены
переменной
15.
Решение системы графическим способому - х=2,
у - х 2 = 0;
Выразим у
через х
y
y=x+2
у=х+2,
2
у= х ;
Построим график
первого уравнения
у=х+2
Построим график
второго уравнения
у= х 2
4
y= х 2
1
-1 0
1 2
Найдем координаты точек
пересечения графиков функций
Ответ: (2; 4);(-1;1)
FokinaLida.75@mail.ru
x
16.
Укажите систему уравнений,которая не имеет решений.
y-10=0
х у 3,
1
2
у
х
1.
у х 2 1,
2
х 5 0.
у х 2 1,
3
у 10 0.
4
ВЕРНО!
x+5=0
ОДНО
решение
ДВА
решения
Все три указанные системы
FokinaLida.75@mail.ru
ПОДУМАЙ!
17.
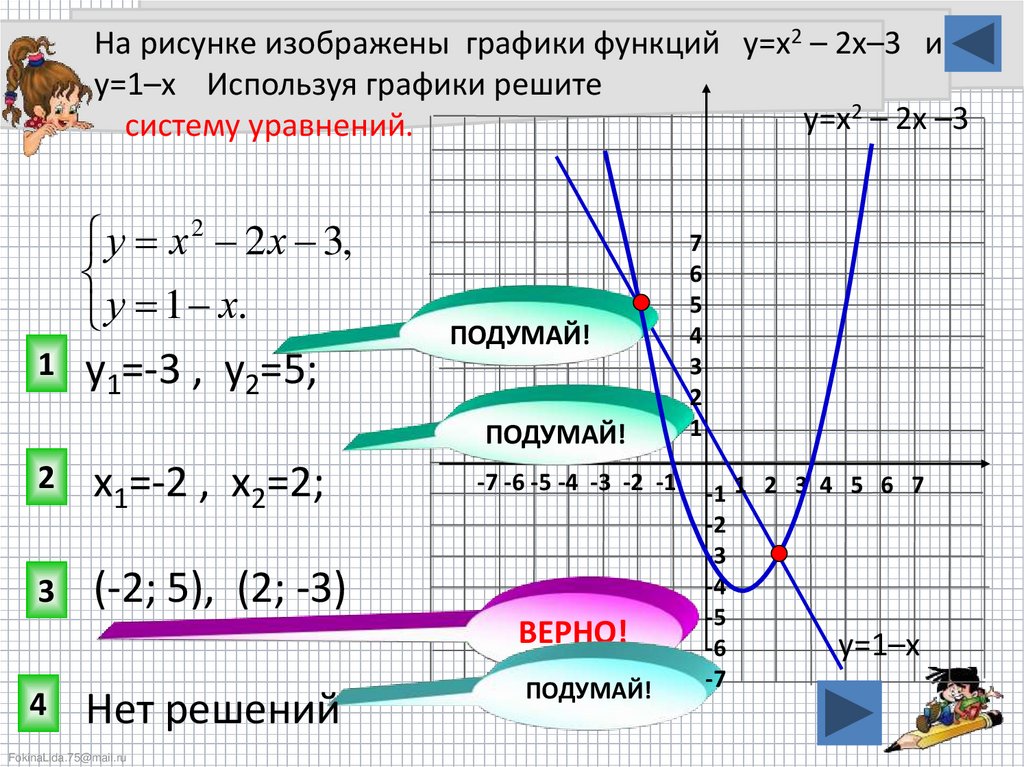
На рисунке изображены графики функций у=х2 – 2х–3 иу=1–х Используя графики решите
у=х2 – 2х –3
систему уравнений.
у х 2 2 х 3,
у 1 х.
1
у1=-3 , у2=5;
ПОДУМАЙ!
ПОДУМАЙ!
2
х1=-2 , х2=2;
3
(-2; 5), (2; -3)
-7 -6 -5 -4 -3 -2 -1
ВЕРНО!
4
Нет решений
FokinaLida.75@mail.ru
ПОДУМАЙ!
7
6
5
4
3
2
1
-1 1 2 3 4 5 6 7
-2
-3
-4
-5
у=1–х
-6
-7
18.
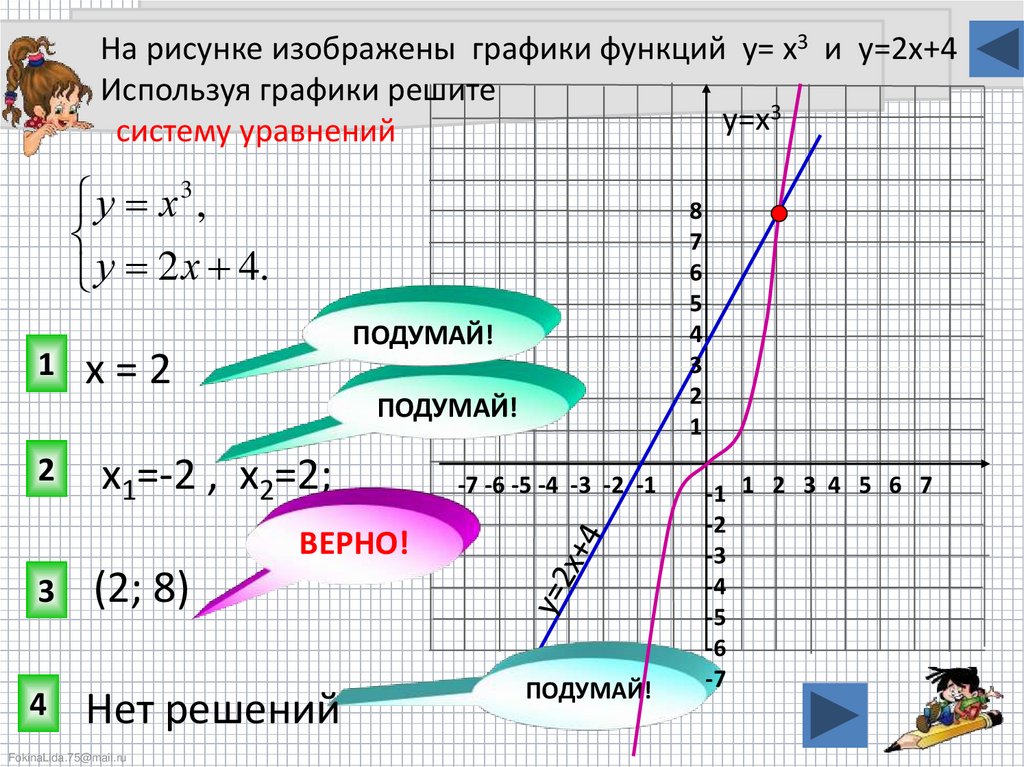
На рисунке изображены графики функций у= х3 и у=2х+4Используя графики решите
3
у=х
систему уравнений
у х3 ,
у 2 х 4.
1
8
7
6
5
4
3
2
1
ПОДУМАЙ!
х=2
ПОДУМАЙ!
2
х1=-2 , х2=2;
-7 -6 -5 -4 -3 -2 -1
ВЕРНО!
3
4
(2; 8)
Нет решений
FokinaLida.75@mail.ru
ПОДУМАЙ!
-1 1 2 3 4 5 6 7
-2
-3
-4
-5
-6
-7
19.
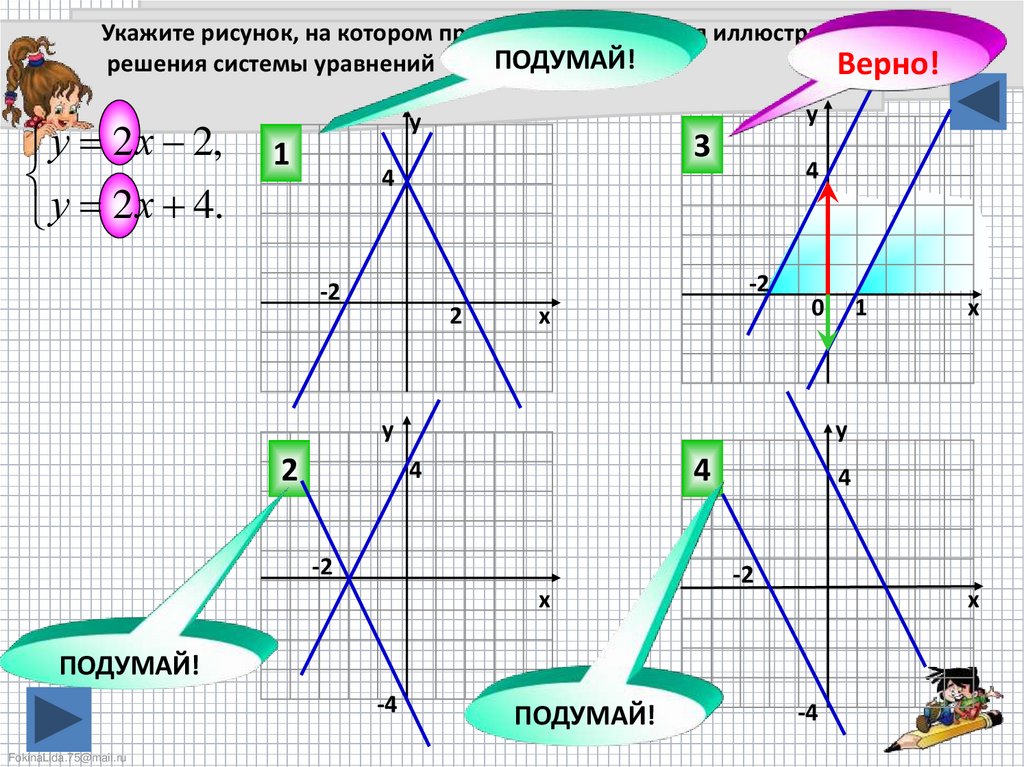
Укажите рисунок, на котором приведена графическая иллюстрацияПОДУМАЙ!
решения системы уравнений
Верно!
у 2 х 2,
у 2 х 4.
у
у
1
3
4
4
-2
-2
2
х
0
у
2
4
-2
х
4
-2
х
ПОДУМАЙ!
FokinaLida.75@mail.ru
х
у
4
-4
1
ПОДУМАЙ!
-4
20.
Решить систему уравненийу х 3;
х 8
FokinaLida.75@mail.ru
21.
Способ подстановки (алгоритм)• Из какого-либо уравнения выразить одну
переменную через другую
• Подставить полученное выражение для
переменной в другое уравнение
• решить полученное уравнение
• Сделать подстановку найденного значения
переменной и вычислить значение второй
переменной
• Записать ответ
FokinaLida.75@mail.ru
22.
Решение системы уравненийспособом подстановки
Выразим х через у
х=2+у,
у у2 0
х=2+у,
х - у=2,
х у2 2 ;
2 у у2 2
Подставим
Решим
уравнение
у у 2 0;
у (1 у ) 0;
х 2 у,
у 0,
у 1
Подставим
х 2 0,
у 0;
х 2 1,
у 1
х 2,
у 0;
х 3,
у 1
у=0 или 1-у=0
у=1
Ответ:(2;0);(3;1).
FokinaLida.75@mail.ru
23.
Способ сложения (алгоритм)• Уравнять модули коэффициентов при какойнибудь переменной
• Сложить почленно уравнения системы
• Составить новую систему: одно уравнение новое,
другое - одно из предыдущей системы
• Решить новое уравнение и найти значение одной
переменной
• Подставить значение найденной переменной во
второе уравнение и найти значение другой
переменной
• Записать ответ: х=…; у=… .
FokinaLida.75@mail.ru
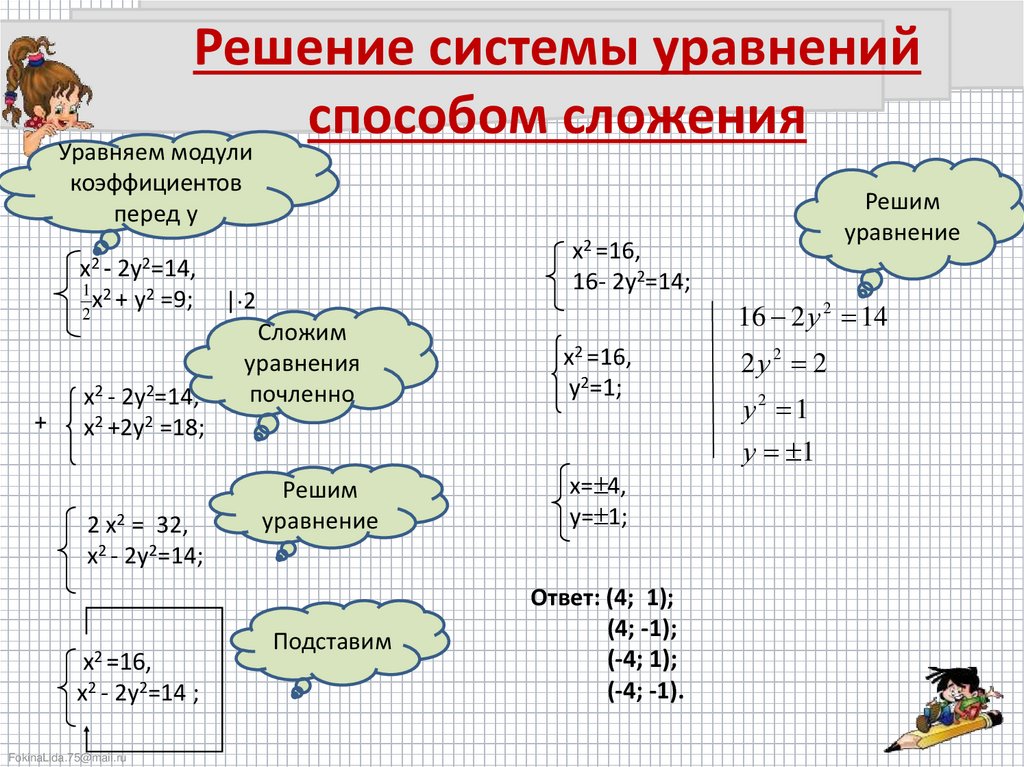
24.
Решение системы уравненийспособом
сложения
Уравняем модули
коэффициентов
перед у
х2 -
+
х2 =16,
16- 2у2=14;
2у2=14,
1 2
х +
2
у2 =9;
х2 - 2у2=14,
х2 +2у2 =18;
2 х2 = 32,
х2 - 2у2=14;
х2 =16,
х2 - 2у2=14 ;
FokinaLida.75@mail.ru
Решим
уравнение
| 2
Сложим
уравнения
почленно
16 2 у 2 14
х2 =16,
у2=1;
2 у2 2
у2 1
у 1
Решим
уравнение
Подставим
х= 4,
у= 1;
Ответ: (4; 1);
(4; -1);
(-4; 1);
(-4; -1).
25.
Метод замены4
х у
8
х у
Пусть
FokinaLida.75@mail.ru
12
3,
х у
18
1
х у
1
a
х у
1
b
x y
26.
Самостоятельная работаРешите графически систему
уравнений
3б
у х 2 2,
у х 4
Решите систему методом
сложения
ху х 56,
х 2 2 у 2 14,
х 2 у 2 9,
2
4б
4б 2
5б
ху у 54
у х 4
х 2 у 18
Решите систему методом подстановки
3б
ху х 2 4,
у х 2
4б
у 3х 0,
2 2
х у 40
Решите систему методом замены
5б
FokinaLida.75@mail.ru
8
6
х у х у 2,
9 10 8
х у х у
6б
1
1
х у 1 х у 1 2,
4
3
7
х у 1 х у 1
27.
Самостоятельная работа (ответы)Решить графически систему
уравнений
3б
(2; 6)
(-1; 3)
Решите систему методом
сложения
4б
4б
5б
нет
(4;1) (4; -1)
решений (-4; 1) (-4; -1) (8; 6) (-7;-9)
Решите систему методом подстановки
3б
4б
(2; 6) (-2;-6)
(-2; 0) (1;3)
Решите систему методом замены
5б
6б
(2,5 ; -0,5)
FokinaLida.75@mail.ru
(1; 1)
28.
«Человека, умеющего наблюдать ианализировать, обмануть просто
невозможно. Его выводы будут
безошибочны, как теоремы Евклида»
Артур Конан Дойл
FokinaLida.75@mail.ru
29.
Решите систему уравненийх 5 у 5,
2
2
х
25
у
75
FokinaLida.75@mail.ru
30.
Решите систему уравненийх 4 у 2,
3
3
х
64
у
56
FokinaLida.75@mail.ru
31.
Домашнее задание:1. № 158 стр. 204 - Сборник
х у 2,
2 х у 2
2
FokinaLida.75@mail.ru
32.
1. Собирай по ягодке – наберёшь кузовок;2. Дело мастера боится;
3. Старая песня на новый лад;
4. У страха глаза велики;
5. Через тернии к звездам;
6. Грамоте учиться всегда пригодится;
7. Где хотенье – там уменье;
8. Терпение и труд всё перетрут;
9. Ах, как я устал от этой суеты;
10. Без труда не вытащишь рыбку из пруда.
FokinaLida.75@mail.ru
33.
FokinaLida.75@mail.ru34.
1. Найдите х+у :x y 16,
x y 2.
2
FokinaLida.75@mail.ru
2
35.
2. Найдите xy :x y 5,
1
10
1
.
x
y
11
FokinaLida.75@mail.ru
36.
3. Подберите решение системыуравнений:
( x y 2) ( y 1) 0,
(
x
1
)(
y
1
)
0
.
2
FokinaLida.75@mail.ru
2
37.
4. Используя теорему Виета и теорему,обратную теореме Виета, решить систему
уравнений:
x y 3,
xy
2
.
FokinaLida.75@mail.ru
38.
5.Используя графическое
представление,
определить, сколько
решений имеет система:
x y 16,
2
y x 4.
2
FokinaLida.75@mail.ru
2





























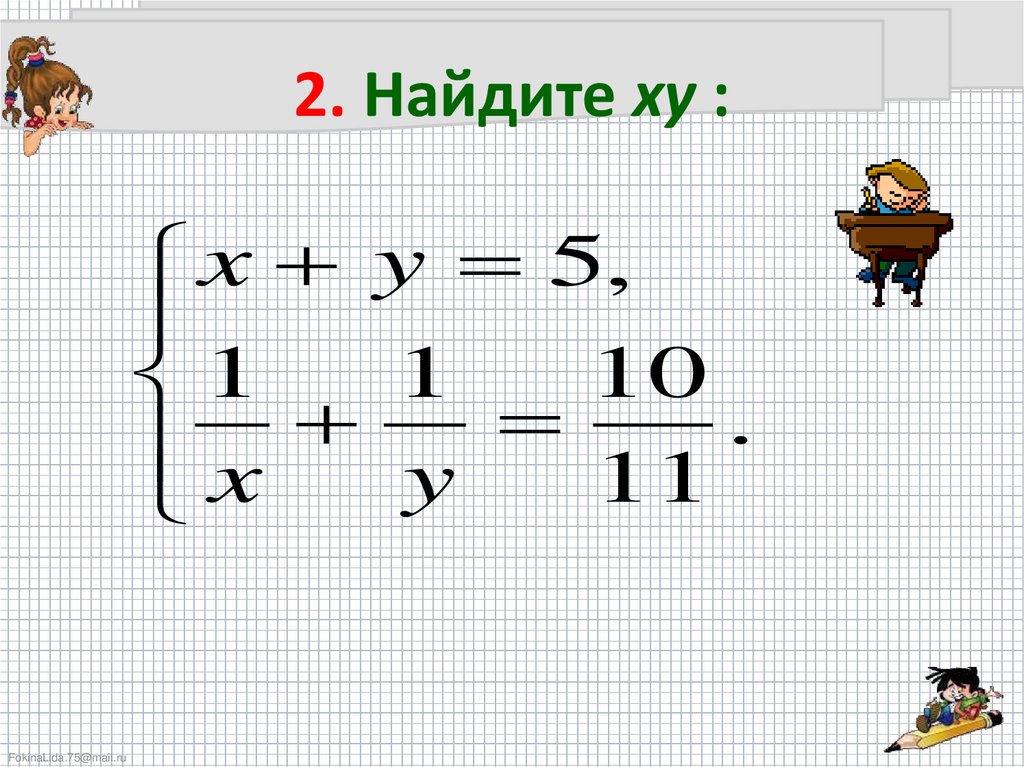



 mathematics
mathematics








