Функция и ее свойства

1. Функция и ее свойства

X
Y
X
0
4
7
Y
0
-4
-7
y
Y=kX+b,
Y=kX,
Y=aX2+bX+c
o
Функция и ее свойства
Х

2.

Х
Y
Функция – зависимость переменной
Y от переменной Х, при которой
каждому значению Х соответствует
единственное значение Y.
Y = f (x)
Переменная Х – аргумент или
независимая переменная;
переменная Y – зависимая
переменная или функция от
переменной Х.

3. O 1 x

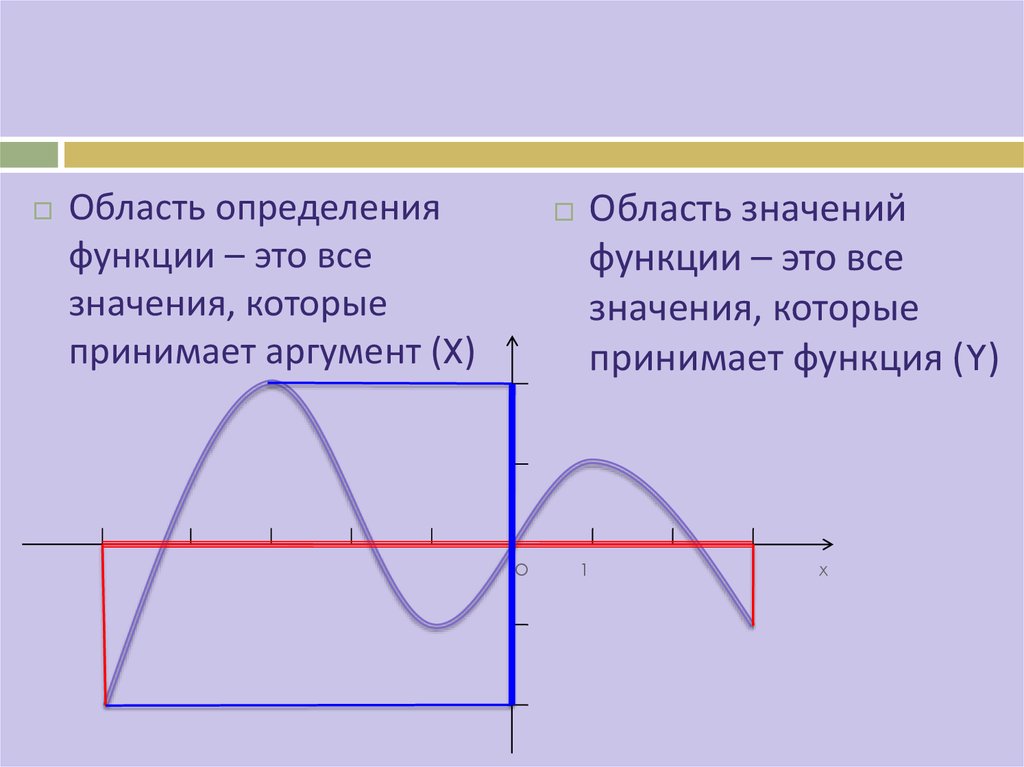
Область определения
функции – это все
значения, которые
принимает аргумент (X)
O
Область значений
функции – это все
значения, которые
принимает функция (Y)
1
x

4. Область определения функции D(x)=[-4 ; 4] или х є [-4 ;4 ]

Y
x
Область определения функции
D(x)=[-4 ; 4]
или
х є [-4 ;4 ]

5. E(y) = [-2;3] или y є [-2;3]

Y
x
Область значений функции
E(y) = [-2;3] или y є [-2;3]

6. Нахождение значения функции при заданном значении аргумента

Найти значение функции F(x) =
при х = -1.
Решение:
F(-1) =
Ответ: -1.

7. Нахождение значения аргумента при заданном значении функции

Найдите значения аргумента, при
которых функция f(x) = (x+5)(2x-3)
принимает значение, равное 0.
Решение:
(x+5)(2x-3) = 0,
Х+5 = 0 или 2х+3 = 0,
Х= -5
2х=-3
х=-1,5
Ответ: -5; -1,5.

8. Как найти D(x)

f (x) = 3х-2
1.
f (x) =
2.
f (x) =
3х+1=0,
3х = -1,
Х=
.
D(x) = (-∞;
Если функция задана уравнением,
содержащим целое выражение, то
D(x) = (-∞;+∞).
Если функция задана уравнением,
содержащим дробное выражение,
то , чтобы найти D(x), надо:
) U(
;+∞)
Найти значения х, при которых
знаменатель равен 0;
Исключить из промежутка (-∞;+∞)
те значения х, которые обращают
знаменатель в 0.