Числовые неравенства. 8 класс

1. Числовые неравенства.

ЧИСЛОВЫЕ НЕРАВЕНСТВА.
8 класс

2. Сравнение действительных чисел.

СРАВНЕНИЕ ДЕЙСТВИТЕЛЬНЫХ ЧИСЕЛ.
1.
2.
3.
4.
5.
6.
Как сравнить действительные числа?
Как сравнить положительные и
отрицательные числа?
Как сравнить десятичные дроби?
Как сравнить обыкновенные дроби?
Как сравнить обыкновенную и
десятичную дроби?
Как сравнить два отрицательных числа?

3. Сравнение действительных чисел.

СРАВНЕНИЕ ДЕЙСТВИТЕЛЬНЫХ ЧИСЕЛ.
Какое общее правило вы
знаете для сравнения
действительных чисел?

4. Сравнить:

а) -15 * 0
г) ¾ * ⅞
б) 3 ⁸⁄₁₁ * 0
в) ²⁸⁄₄ * 2
д) 1,25 * 1¼
е) 0,6 * ³/₇
ж) - ½ * -⅓
з) – 0,07 * - ³/₅₀
и) -5,6786 * - 5,679

5. Определение:

Число а > в, если разность
а – в положительное число;
Число а < в, если разность
а – в отрицательное число

6. Итог урока:

Сформулируйте
универсальное правило
сравнения чисел.

7. Устная работа:

1. Сравнить а и в, если а – в равно:
а) – 3; б) 0,2; в) 0; г) (-3)⁶; д) в - а;
е) 2√3 - 3
2. Расположите в порядке
возрастания числа:
1,2; 1⅓; 1²/₇; 1,4; 1¹⁄₉

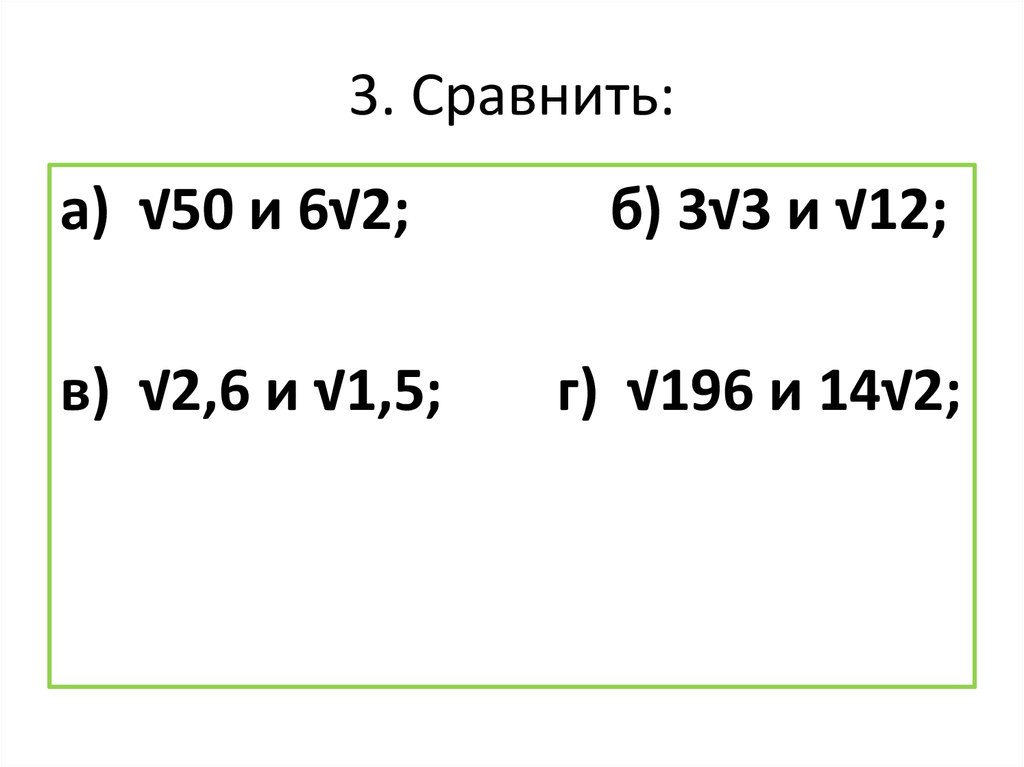
8. 3. Сравнить:

а) √50 и 6√2;
в) √2,6 и √1,5;
б) 3√3 и √12;
г) √196 и 14√2;

9. Проверочная работа.

Вариант 1. Докажите неравенство:
а) (6у -1)(у +2 )< (3у + 4)(2у + 1);
б) 4(х +2) < (х + 3)² - 2х.
Вариант 2. Докажите неравенство:
а) (3у – 1 )(2у +1) > (2у – 1)(2 + 3у);
б) (х – 5)² + 3х > 7(1-х).