Системы содержащие нелинейные уравнения

1.

2.

1. Определите, из какого уравнения системы и какую переменную удобнее
выразить:
а)
2 x y 3,
3x 2 y 1;
б)
4 x 5 y 1,
2 x y 4;
в)
a 3b 2,
a 7b 4;
г)
3a 2b 1,
5a 6b 8.

3.

2. Определите, каким способом удобнее решить систему уравнений. Ответ
объясните.
сложение
подстановка
а)
x 3 y,
2 x y 5;
в)
подстановка
б)
2 x 3 y 4,
x 5 y 7;
3x 7 y 2,
5x 2 y 1;
•2
•7
сложение
г)
2 x 5 y 8,
4 x 3 y 6.
•3
•5

4.

Решить систему способом сложения:
x 2 y 2 4,
y 2 x 2
y = 2 - 2x
?
Каким способом можно решить?
x2+(2-2x)2=4
y=2 - 2x
x2 + 4 – 8x + 4x2 = 4
5x2 – 8x = 0
x(5x - 8) = 0
x1 = 0, x2 = 1,6.
y1 = 2 – 2 • 0 = 2;
y2 = 2 – 2 • 1,6 = -1,2.
Ответ: ( 0; 2), ( 1,6; - 1,2)

5.

Выясним, что представляет собой график уравнения x2 + y2 = 4
Пусть М(a; b) – произвольная точка графика данного уравнения
(a; b) – решение уравнения x2 + y2 = 4 , т.е. верно равенство a2 + b2 = 4
y
Расстояние от точки М до начала координат:
По тереме Пифагора
М (a; b)
т.. к. a2 + b2 = 4, то
b
0
a
ОМ 2 = a2 + b2
ОМ 2 = 4
x
ОМ = 2
График уравнения x2 + y2 = 4 есть окружность
с центром в начале координат и с радиусом,
равным 2.
В ы в од 1 . Графиком уравнения вида x2 + y2 = r2, где r > 0, является окружность
с центром в начале координат и радиусом r.
В ы в од 2 . Система, в которой одно из уравнений является линейным, а второе
имеет вид x2 + y2 = r2, где r > 0, может иметь одно, два решения или вообще не
иметь решений.

6.

№ 654 (а, г)
x y 0,
2
2
x
y
16;
г)
y x,
2
2
x
x
16;
2x2 = 16;
x2 = 8;
x = 8 ;
y = 8 .
О т в е т : ( 8; 8) , ( 8; 8) .

7.

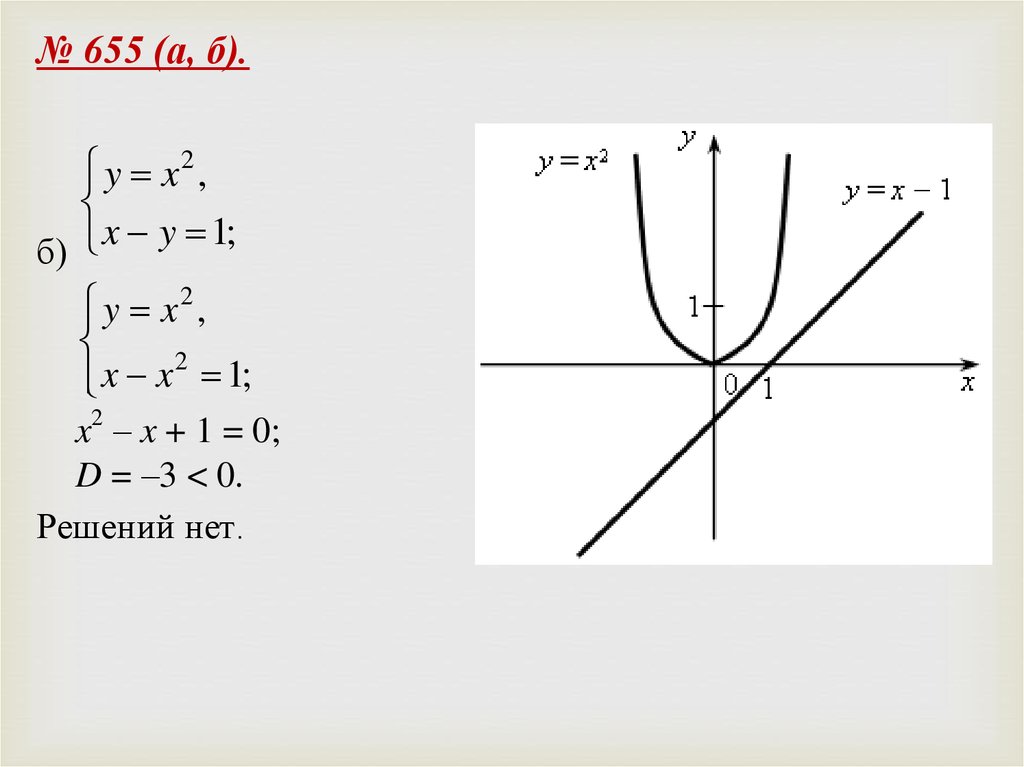
№ 655 (а, б).
y x2 ,
x y 1;
б)
y x 2 ,
2
x x 1;
x2 – x + 1 = 0;
D = –3 < 0.
Решений нет.

8.

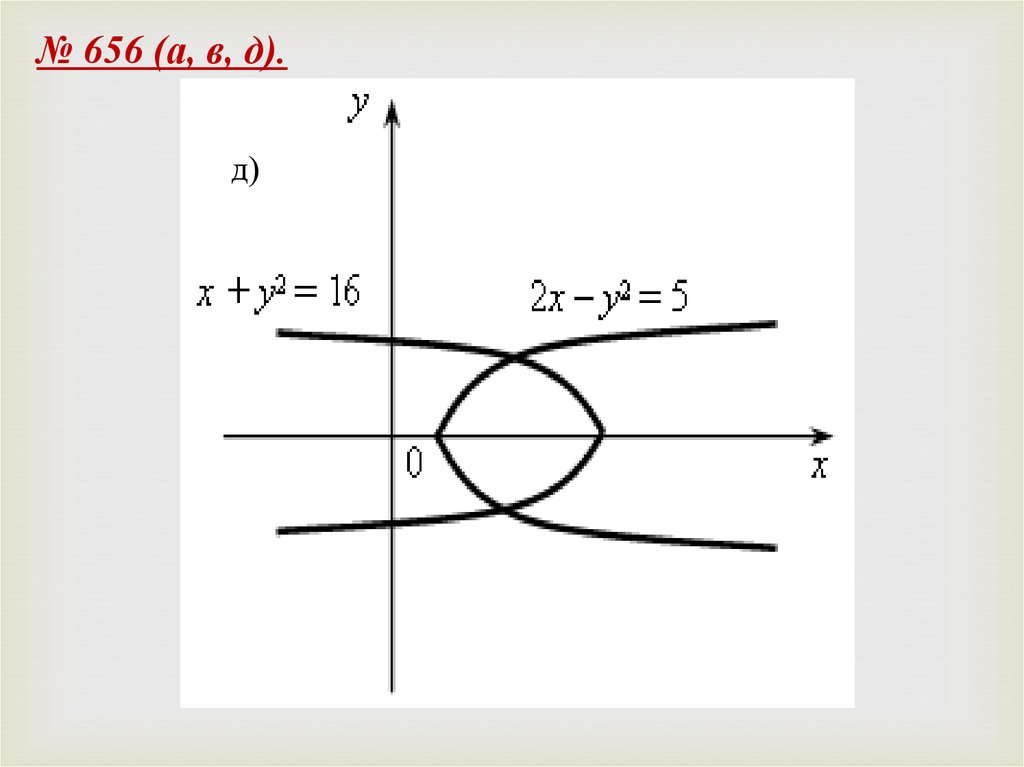
№ 656 (а, в, д).
в)
д)
а)

9.

– Каков алгоритм решения систем уравнений способом
подстановки?
– Любую ли систему уравнений можно решить способом
сложения? Способом подстановки?
– Можно ли решить способом сложения систему,
содержащую нелинейные уравнения?
– Что представляет собой график уравнения вида
x2 + y2 = r2, где r > 0?

10.

№ 654 (б, в), 655 (в), 656 (б, г, е).