Линейные неоднородные дифференциальные уравнения n-го порядка

1. Линейные неоднородные дифференциальные уравнения n-го порядка

Общий вид линейного дифференциального
уравнения n-го порядка такой:
y( n ) a1( x )y( n 1 ) a2 ( x )y( n 2 )
an ( x )y f ( x )
a1( x ),a2 ( x ), ,an ( x ), f ( x ) - заданные функции от x или
числа.
Это уравнение линейно относительно неизвестной
функции y(x) и ее производных (т.е. содержит их в
первой степени).
( 1)

2. Пример линейного дифференциального уравнения второго порядка

y 5 y 6 y ( 2 x 1 )e
x

3. Определение. Если правая часть (не равна нулю тождественно), то линейное уравнение (1) называется неоднородным.

Определение. Если правая часть
f ( x ) 0 (не равна
нулю тождественно), то линейное уравнение (1)
называется неоднородным.
Пример
y 4 y 18 y (2 x 1)e 3 x

4. Теорема о структуре линейного неоднородного дифференциального уравнения n-го порядка

Общее решение y ( x) линейного
неоднородного дифференциального уравнения (1)
равно сумме общего решения Y ( x) соответствующего
ему однородного уравнения (2) и какого-нибудь
частного решения y ( x) данного неоднородного
уравнения (1).
y ( x ) Y ( x) y ( x )
Y ( x) - общее решение однородного уравнения,
y ( x) - частное решение неоднородного уравнения

5. Доказательство (для случая n = 2)

Докажем, что функция y( x) будет удовлетворять
обоим условиям определения общего решения
дифференциального уравнения 2-го порядка.
Y ( x) C1 y1 ( x) C2 y2 ( x)
1.
где y1 ( x), y2 ( x) - ФСР однородного уравнения.
y( x) Y ( x) y ( x) C1 y1 ( x) C2 y2 ( x) y ( x)
содержит 2 произвольные постоянные.

6. Для доказательства подставим функцию в линейное неоднородное дифференциальное уравнение второго порядка .

Получим
C y ( x) C y ( x) y ( x) a ( x) C y ( x) C y ( x) y ( x) a ( x) C y (x) C y (x) y (x) f (x)
1 1
2 2
1
1 1
2 2
2
1 1
2 2
Преобразуем:
C1 y1 ( x) a1 ( x) y 1 ( x) a2 ( x) y1 ( x) C2 y2 ( x) a1 ( x) y 2 ( x) a2 ( x) y2 ( x)
y ( x) a1 ( x) y ( x) a2 ( x) y ( x) f ( x)
Так как y1 ( x), y2 ( x) - это решения однородного уравнения, то
y1 ( x) a1 ( x) y 1 ( x) a2 ( x) y1 ( x) 0, y2 ( x) a1 ( x) y 2 ( x) a2 ( x) y2 ( x) 0

7. И так как - решение неоднородного уравнения, то

И так как y ( x) - решение неоднородного уравнения, то
y ( x) a ( x) y ( x) a ( x) y ( x) f ( x)
1
2
то есть
f ( x) f ( x ) .
Значит функция y( x) C1 y1 ( x) C2 y2 ( x) y ( x)
при подстановке в неоднородное
дифференциальное уравнение превращает его в
тождество, то есть является решением этого
уравнения при любых значениях произвольных
постоянных C1 , C2 .

8. 2. Пусть заданы начальные условия:

y ( x0 ) y0
y ( x0 ) y1
(3),
где
y0 , y1 - некоторые числа.
Покажем, что из функции y( x) C1 y1 ( x) C2 y2 ( x) y ( x)
можно получить частное решение, удовлетворяющее
начальным условиям (3).
Для нахождения значений произвольных постоянных
составим систему двух уравнений с двумя
неизвестными C1 , C2 , подставив функцию y(x) в
начальные условия (3):

9. Получим:

C1 y1 ( x0 ) C2 y2 ( x0 ) y ( x0 ) y0
C1 y1 ( x0 ) C2 y2 ( x0 ) y ( x0 ) y1
или
C1 y1 ( x0 ) C2 y2 ( x0 ) y0 y ( x0 )
C1 y1 ( x0 ) C2 y2 ( x0 ) y1 y ( x0 )
Главный определитель этой системы:
y1 ( x0 )
y1 ( x0 )
y2 ( x0 )
W ( x0 )
y2 ( x0 )

10. - это определитель Вронского системы решений .

W ( x0 ) - это определитель Вронского
системы решений y1 ( x), y2 ( x) .
По условию решения
оставляют ФСР
(фундаментальную систему решений) однородного
дифференциального уравнения, то есть они
линейно независимы.
Следовательно, по необходимому условию
линейной независимости W ( x0 ) 0 .
А если основной определитель системы линейных
уравнений не равен нулю, эта система имеет
единственное решение: C1 C1o , C2 C2o .
Если эти значения произвольных постоянных
подставить в функцию y(x) , то мы получим частное
решение yчастн. ( x) C1o y1 ( x) C2o y2 ( x) y ( x) ,

11.

удовлетворяющее начальным условиям (3).
Таким образом, функция y(x) удовлетворяет и
второму условию определения общего решения
дифференциального уравнения второго порядка,
значит она является общим решением
дифференциального уравнения (1), что и
требовалось доказать.

12. Линейные неоднородные дифференциальные уравнения n-го порядка с постоянными коэффициентами.

y ( n) a1 y ( n 1)
an y f ( x)
где a1 ,a2 , ,an - действительные числа.
Например,
y 5 y 6 y (2 x 3)e7 x

13. Метод неопределенных коэффициентов для отыскания частного решения линейных неоднородных дифференциальных уравнений n-го порядка

с постоянными коэффициентами.
Этот метод применим, если правая часть линейного
неоднородного дифференциального уравнения (1)
f ( x) имеет специальный вид.
Рассмотрим два случая специального вида правой
части f ( x) .

14. 1 случай.

f ( x) Pm ( x)e x
где Pm ( x) b0 xm b1 xm 1 bm - многочлен степени m.
а). Если не является корнем характеристического
уравнения, то частное решение y ищем в виде
произведения y ( Axm Bxm 1 M )e x -
m
m 1
многочлена Ax Bx M той же степени m c
неопределенными коэффициентами A, B, , M на
функцию e x , какая была в правой части уравнения f ( x) .

15. 1 случай.

f ( x) Pm ( x)e x
где Pm ( x) b0 xm b1 xm 1 bm - многочлен степени m.
б). Если является корнем характеристического
уравнения кратности r (т.е. число
встречается среди
корней характеристического уравнения ровно r раз), то частное
решение y ищем в виде произведения
y ( Axm Bxm 1
M )e x xr -
многочлена Axm Bxm 1 M той же степени m c
неопределенными коэффициентами A, B, , M на
функцию e x , какая была в правой части уравнения f ( x)
и на x r .

16. Соответствие многочлена в правой части уравнения и многочлена с неопределенными коэффициентами в частном решении :

многочлен в правой части
2x 1
5x
x 2 3x 7
многочлен с неопределенными
коэффициентами в частном
решении
Ax B
Ax2 Bx C
3x2 x
8x 2
5
A

17. Примеры

1. Найти общее решение.
y 3 y (10 x 1)e2 x
Решение.
1). Решаем однородное уравнение, соответствующее
данному неоднородному:
y 3 y 0 .
Решение ищем в виде y ekx , составляем
характеристическое уравнение:
k 2 3k 0
k1 0, k2 3 - корни характеристического
уравнения, значит общее решение однородного уравнения:
Y C1 C2e 3 x

18. 2). Ищем частное решение неоднородного уравнения

По условию f ( x) (10 x 1)e2 x , здесь
(10 x 1) - многочлен первой степени, значит в частном
решении многочлен с неопределенными
коэффициентами будет Ax B , и в целом частное
решение имеет вид:
y ( Ax B)e2 x,
так как e x сейчас e 2 x , значит 2 - не является корнем
характеристического уравнения (нет совпадений) - 1 случай
а).
Дальше наша задача - только найти неизвестные
коэффициенты A, B.
Найдем их из условия, что
является
решением неоднородного уравнения, т.е. при
подстановке в это уравнение превращает его в
тождество.

19. Займемся этой подстановкой.

Сначала найдем производные.
y Ae2 x 2( Ax B)e2 x (2 Ax 2B A)e2 x
y 2 Ae2 x 2(2 Ax 2B A)e2 x
Подставим их в данное уравнение:
2 Ae2 x 2(2 Ax 2B A)e2 x 3(2 Ax 2B A)e2 x (10x 1)e2 x
2x
e
Разделим левую и правую часть на
и приведем
подобные:
10 Ax 10B 7 A 10 x 1

20. Это равенство выполняется при любых x, это значит, что будут равны коэффициенты при одинаковых степенях x и свободные члены в

левой и правой
части,
то есть получим систему двух уравнений
относительно двух неизвестных A и B:
10 A 10
10 B 7 A 1
Из этой системы получаем:
A 1, B 0,8
Значит, частное решение найдено: y ( x 0,8)e2 x .

21. По теореме о структуре линейного неоднородного дифференциального уравнения общее решение равно

сумме общего решения однородного уравнения и
частного решения неоднородного уравнения.
По этой теореме в нашей задаче получаем ответ:
y C1 C2e 3 x ( x 0,8)e2 x

22. Примеры

2. Найти общее решение.
y 2 y y 5e x
Решение.
1). Решаем однородное уравнение, соответствующее
данному неоднородному:
y 2 y y 0 .
Решение ищем в виде y ekx , составляем
характеристическое уравнение:
2
k 2 2k 1 0 или (k 1) 0
k1,2 1 - два равных корня характеристического
уравнения, значит общее решение однородного уравнения:
Y C1e x C2e x x

23. 2). Ищем частное решение неоднородного уравнения

По условию f ( x) 5e x , здесь
5 - многочлен нулевой степени, значит в частном
решении многочлен с неопределенными
коэффициентами будет A, и в целом частное решение
имеет вид:
y Ae x x2 ,
так как e x сейчас e x, значит 1 , и это число
является корнем характеристического уравнения
кратности 2 (два совпадения) - 1 случай, б).
Дальше наша задача - найти неизвестный коэффициент
A.

24. Подставим в исходное уравнение

Сначала найдем производные.
y A ( e x x2 2 xe x ) Ae x ( x 2 2 x)
y Ae x ( x2 2 x) Ae x ( 2 x 2) Ae x ( x 2 4 x 2)
Подставим их в данное уравнение:
Ae x ( x2 4 x 2) 2 Ae x ( x2 2 x) Ae x x2 5e x
Преобразуем: 2 A 5,
и частное решение:
A 2,5
y 2,5 e x x2

25. По теореме о структуре линейного неоднородного дифференциального уравнения общее решение равно

сумме общего решения однородного уравнения и
частного решения неоднородного уравнения.
По этой теореме в нашей задаче получаем ответ:
y C1e x C2e x x 2,5 e x x2

26. Примеры

3. Найти общее решение.
y 5 y 30 x2 8x 1
Решение.
1). Решаем однородное уравнение, соответствующее
данному неоднородному:
y 5 y 0 .
Решение ищем в виде y ekx , составляем
характеристическое уравнение:
k 2 5k 0
k1 0, k2 5 - корни характеристического
уравнения, значит общее решение однородного уравнения:
Y C1 C2e 5 x

27. 2). Ищем частное решение неоднородного уравнения

По условию f ( x) 10 x2 8x 1 или f ( x) (10 x2 8x 1) e0 x ,
здесь 10 x2 8x 1 - многочлен второй степени, значит в
частном решении многочлен с неопределенными
коэффициентами будет Ax2 Bx C , и в целом частное
решение имеет вид:
y* ( Ax2 Bx C )e0 x x
x
e
так как
- это e0 x , значит 0 , а 0 является корнем
характеристического уравнения кратности 1 ( одно
совпадение) - 1 случай, б).
Раскроем скобки:
Дальше наша задача - найти неизвестные
коэффициенты A, B, C .
Найдем их из условия, что y Ax3 Bx 2 Cx является
решением неоднородного уравнения, т.е. при подстановке в это
уравнение превращает его в тождество.

28. Подставим в исходное уравнение .

Подставим
уравнение
в исходное
.
Сначала найдем производные.
y 3 Ax 2 2Bx C
y 6 Ax 2B
Подставим их в данное уравнение:
6 Ax 2B 5(3 Ax2 2Bx C ) 30 x2 8x 1
Преобразуем: 15 Ax2 (6 A 10B) x 2B 5C 30x2 8x 1
Приравняем коэффициенты при одинаковых степенях x и
свободные члены в левой и правой части, получим систему трех
уравнений относительно неизвестных A,B,C :

29. Система имеет вид:

15 A 30
6 A 10 B 8
2 B 5C 1
Из этой системы получаем: A 2, B 2, C 1
Значит, частное решение найдено:
y 2 x3 2 x 2 x

30. По теореме о структуре линейного неоднородного дифференциального уравнения общее решение равно

сумме общего решения однородного уравнения и
частного решения неоднородного уравнения.
По этой теореме в нашей задаче получаем ответ:
y C1 C2e 5 x 2 x3 2 x2 x

31. 2 случай

f ( x) Pm ( x)e x cos x или
f ( x) Pm ( x)e x sin x
или
f ( x) Pm1 ( x)e x cos x Pm2 ( x)e x sin x ,
где Pm ( x) b0 xm b1 xm 1 bm
а) число i не является корнем
характеристического уравнения. Тогда частное решение
ищем в виде:
y* ( A1 xm B1 xm 1
N1 )e x cos x ( A2 x m B2 x m 1
N2 )e x sin x
m max(m1 , m2 ) , если в правой части - многочлены разных
степеней.

32. б). число является корнем характеристического уравнения кратности r.

y* ( A1 xm B1 xm 1
N1 )e x cos x ( A2 x m B2 x m 1
N 2 )e x sin x x r

33. Примеры.

1). Найти общее решение
y 2 y 5cos x
Решаем однородное уравнение, соответствующее
данному неоднородному:
y 2 y 0 .
Решение ищем в виде
, составляем
характеристическое уравнение:
k 2 2k 0
k1 0, k2 2 - корни
характеристического уравнения, значит общее
решение однородного уравнения:
Y C1 C2e 2 x

34. 2). Ищем частное решение неоднородного уравнения.

2). Ищем частное решение y * неоднородного
уравнения.
По условию f ( x) 5cos x , здесь 5 - многочлен
нулевой степени, значит в частном решении
многочлены с неопределенными коэффициентами
будут A и B , и в целом частное решение имеет
вид:
y* A cos x B sin x ,
0x
так как e x cos x - это e cos x в нашей задаче,
значит i 0 1 i i - это число не является
корнем характеристического уравнения - 2 случай,
а).
Дальше наша задача - найти неизвестные
коэффициенты A и B .

35. Подставим в исходное уравнение .

Подставим
уравнение
в исходное
.
Сначала найдем производные.
y* A sin x B cos x
y* A cos x B sin x
Подставим их в данное уравнение:
A cos x B sin x 2( Asin x B cos x) 5cos x
Преобразуем:
( A 2B)cos x ( B 2 A)sin x 5cos x
Получим систему двух уравнений относительно A и B:
A 2 B 5
B 2 A 0

36. Из этой системы получаем:

A 1, B 2
Значит, частное решение найдено:
y* cos x 2sin x .
(Заметим, что в
частном решении
не было sin x, а в полученном
есть и cos x и
).
Как мы знаем общее решение неоднородного уравнения
получается так:
Значит ответ:
y C1 C2e 2 x cos x 2sin x

37. Пусть линейное дифференциальное уравнение имеет вид:

1. y a1 y a2 y f1 ( x) f 2 ( x)
Тогда частное решение данного уравнения равно
сумме частных решений: y* y1* y2* , где
y1* - частное решение уравнения
y a1 y a2 y* f1 ( x)
y2* - частное решение уравнения y a1 y a2 y* f 2 ( x)

38. Пример

Найти вид общего решения:
y 6 y 12 y 8 y 2 xe 2 x 5e 2 x cos 2 x sin 2 x

39. Решение

1. Найдем общее решение однородного дифференциального
уравнения:
y 6 y 12 y 8 y 0
y ekx ,
k 3 6k 2 12k 8 0 ( k 2)3 0 k1,2,3 2
Y C1e 2 x C2 xe 2 x C3 x 2e 2 x - общее решение
однородного уравнения

40. Найдем вид частного решения ( - корни характеристического уравнения)

Найдем вид частного решения
( k1,2,3 2
- корни характеристического уравнения)
y 6 y 12 y 8 y 2 xe 2 x 5e 2 x cos 2 x sin 2 x
f1 ( x )
1. y1* ( Ax B)e 2 x x3
f2 ( x )
f3 ( x )
( 2 три совпадения)
2 x
2 x
2. y2* Ae
cos
2
x
B
e
sin 2 x ( i 2 2i - совпадений нет)
1
1
3. y3* A2 cos 2 x B2 sin 2 x
( i 2i - совпадений нет)
y* y1* y2* y3*
2 x
y* ( Ax B)e 2 x x3 Ae
cos 2 x B1e 2 x sin 2 x A2 cos 2 x B2 sin 2 x
1
y Y y*
2 x
y C1e 2 x C2 xe 2 x C3 x 2e 2 x ( Ax B)e 2 x x3 Ae
cos 2 x B1e 2 x sin 2x A2 cos 2x B2 sin 2x
1
- это вид общего решения

41. Пример.

Найти общее решение y 2 y H sin x
1. y 2 y 0 Y C1 cos x C2 sin x
2. y 2 y H sin x
2a.
y* A cos x B sin x,
y* A sin x B cos x,
y* A 2 cos x B 2 sin x
A 2 cos x B 2 sin x 2 ( A cos x B sin x) H sin x
A( 2 2 )cos x B( 2 2 )sin x H sin x
A 0
A( 2 2 ) 0
H
*
y
sin x
H
2
2
2
2
B( ) H
B 2 2
y C1 cos x C2 sin x
H
sin x
2
2

42. 2b.

y 2 y H sin x
2b.
.
y* ( A cos x B sin x) x,
y* ( A sin x B cos x) x A cos x B sin x,
y* ( A 2 cos x B 2 sin x) x A sin x B cos x A sin x B cos x
( A 2 cos x B 2 sin x) x 2 A sin x 2 B cos x
( A 2 cos x B 2 sin x) x 2 A sin x 2 B cos x 2 ( A cos x B sin x) x H sin x
2 A sin x 2B cos x H sin x
H
2
A
H
A
Hx
*
y
cos x
2
2
2
2 B 0
B 0
y C1 cos x C2 sin x
Hx
cos x
2

43. Метод вариации произвольных постоянных

Это метод отыскания частного решения линейного
неоднородного дифференциального уравнения
y a1 ( x) y a2 ( x) y f ( x)
a1 ( x), a2 ( x) - функции от x или числа.
(1)

44. Теорема

Если y1 ( x), y2 ( x) - фундаментальная система решений
(ФСР) однородного уравнения
(2)
y a1 ( x) y a2 ( x) y 0,
то функция
y* C1 ( x) y1 ( x) C2 ( x) y2 ( x)
является частным решением неоднородного
уравнения (1), если производные C1 ( x), C2 ( x)
удовлетворяют линейной системе уравнений:
C y C y 0
1 1
2 2
C1 y1 C 2 y2 f ( x)

45. Доказательство

Ищем частное решение неоднородного уравнения (1)
в виде y* C1 ( x) y1 ( x) C2 ( x) y2 ( x) , где C1 ( x), C2 ( x) неизвестные пока функции.
y* C1 y1 C2 y2 C1 y1 C2 y2
У нас две неизвестные функции C1 , C2 , надо два
уравнения для их определения. Одно уравнение
получится из условия, что y * удовлетворяет
уравнению (1), второе уравнение можно задать
произвольно. Зададим его так, чтобы y * имело
наиболее простой вид:
C y1 C2 y2 0
Тогда y* C1 y1 C2 y2 .

46. Найдем вторую производную:

y* C1 y1 C1 y1 C2 y2 C2 y2
Подставим y* , y* , y* в уравнение (1).
C1 y1 C1 y1 C2 y2 C2 y2 a1 ( x)(C1 y1 C2 y2 ) a2 ( x)(C1 y1 C2 y2 ) f ( x)
Запишем его так:
C1 ( y1 a1 y1 a2 y1 ) C2 ( y2 a1 y2 a2 y2 ) C1 y1 C2 y2 f ( x)
Здесь обе скобки равны нулю, так как y1 , y2 - решения
однородного уравнения (2) по условию. Тогда имеем:
C1 y1 C2 y2 f ( x)

47. Таким образом, для того, чтобы функция

y* C1 ( x) y1 C2 ( x) y2
была решением неоднородного уравнения (1),
производные
должны являться решением
следующей системы уравнений:
C y C y 0
1 1
2 2
C1 y1 C 2 y2 f ( x)
Определитель этой системы
(3)
y1
y1
y2
0 , так как
y2
это определитель Вронского системы линейно
независимых решений y1 , y2 уравнения (2), значит
система (3) имеет единственное решение:

48. то есть

C1 1 ( x), C2 2 ( x),
C1 ( x), C2 ( x) найдем интегрированием
C1 ( x) 1 ( x)dx, C2 ( x) 2 ( x)dx
(4).
Окончательно, с учетом (4) частное решение
неоднородного уравнения (1) имеет вид:
y* C1 ( x) y1 C2 ( x) y2

49. Пример

Найти общее решение:
y 4 y
1
cos 2 x
Решение.
y 4 y 0,
y ekx
k 2 4 0, k 2 4,
k1,2 4 ( 1) 4 ( 1) 4 2i
y1 cos2 x, y2 sin 2 x
- ФСР
y C1 cos2 x C2 sin 2 x - общее решение
однородного уравнения.

50. Составим систему уравнений:

В нашем случае эта система имеет вид:
C1 cos 2 x C2 sin 2 x 0
1
2
C
sin
2
x
2
C
cos
2
x
1
2
cos 2 x
Решаем ее: из первого уравнения
C2 sin 2 x ,
C1
cos 2 x
подставим во второе:
2C2 sin 2 2 x
1
2C2 cos 2 x
cos 2 x
cos 2 x
или C2 1 , тогда C1 sin 2 x .
2
2cos 2 x

51. Найдем .

Найдем C1 , C2 .
Интегрируем:
sin 2 x
1 d (cos 2 x) 1
dx
ln | cos 2 x | C1
2cos 2 x
4 cos 2 x
4
1
1
C2
dx x C2
2
2
C1
Подставляем найденные выражения для C1 , C2 в
формулу y C1 y1 C2 y2
Получим
Или
1
1
y ln | cos 2 x | C1 cos 2 x x C2 sin 2 x
4
2
y C1 cos 2 x C2 sin 2 x
cos 2 x
1
ln | cos 2 x | x sin 2 x
4
2
Значит частное решение:
y*
cos 2 x
1
ln | cos 2 x | x sin 2 x
4
2

52. Ответ:

53. Пример 2

Найти общее решение.
ex
y y
1 ex
Решение.
y y 0
k 2 k 0, k1 0, k2 1
y1 1, y2 e x - ФСР
y C1 C2e x - общее решение
однородного уравнения

54. Составим систему уравнений:

В нашем случае эта система имеет вид:
C 1 C e x 0
1
2
x
e
x
C1 0 C2 e
1 ex
Решаем ее: из второго уравнения
1
,
C2
x
1 e
подставим в первое:
x
e
C1
1 ex

55. Найдем .

Найдем C1 , C2 .
Интегрируем:
ex
d (e x 1)
C1
dx
ln(e x 1) C1
x
x
1 e
1 e
C2
dx
dt
dt
dt
ln | t 1| ln | t | C2
x
1 e
(t 1)t
t 1
t
1 ex t
ex t 1
x ln(t 1)
dt
dx
t 1
1
A
B
(t 1)t t 1 t
1
At B (t 1)
(t 1)t
(t 1)t
1 At B (t 1)
t 0: 1 B ( 1)
t 1:
1 A
1
1
1
(t 1)t t 1 t
ln |1 e x 1| ln |1 e x | C2 x ln(1 e x ) C2

56. Определили

C1 ln(e x 1) C1 , C2 x ln(1 e x ) C2
Подставляем найденные выражения для
формулу
,
y ln(e x 1) C1 ( x ln(1 e x ) C2 )e x
или
y C1 C2e x xe x (1 e x )ln(1 e x ) -
это общее решение неоднородного уравнения.
в

57. Уравнение Эйлера

1. xn y ( n) a1xn 1 y ( n 1) ... an 1xy an y f ( x)
x et
x2 y a1xy a2 y 0

58. Продолжение.

x et ,
y x
x2 y a1xy a2 y 0
t ln x
dy dt
1
yt yt e t
dt dx
x
d ( yt e t ) dt
1
y xx
ytt e t yt e t ytt e t yt e t e t e 2t ytt yt
dt
dx
x
e 2t e 2t ytt yt a1et yt e t a2 y 0
ytt yt a1 yt a2 y 0
(k 2 k ) a1k a2 0
k (k 1) a1k a2 0
y e kt

59. Продолжение.

1. Пусть k1 k2
y C1ek1t C2ek2t
x et
y C1x k1 C2 x k2 - общее решение.
Так как x et , e kt x k , поэтому решение сразу
можно искать в виде
y xk
k
Подставить в данное уравнение и сократить на x

60. Продолжение.

x2 y a1xy a2 y 0
y xk
Получится характеристическое уравнение
k (k 1) a1k a2 0
В общем случае для уравнения
xn y ( n ) a1xn 1 y ( n 1) ... an 1xy an y 0
каждое произведение x m y ( m ) заменяется в
характеристическом уравнении на произведение k
убывающих на 1 чисел: k (k 1)(k 2)...(k m 1) .

61. Пример

Найти общее решение
x 2 y 4 xy 6 y 0
y xk
k (k 1) 4k 6 0
k 2 5k 6 0
k1 2, k2 3
y C1x 2 C2 x3

62. Пусть k корень характеристического уравнения кратности r.

y1 ekt , y2 tekt , y3 t 2ekt ,..., yr t r 1ekt , значит
y1 x k , y2 x k ln x, y2 x k (ln x)2 ,..., y2 x k (ln x)r 1 ,
так как t ln x

63. Пример

Найти общее решение
x 2 y xy y 0
y xk
k (k 1) k 1 0
k 2 2k 1 0
(k 1) 2 0
k1,2 1
y1 x, y2 x ln x,
y C1x C2 x ln x

64. Случай комплексно-сопряженных корней характеристического уравнения

k1,2 i
1.
y1 e t cos t , y2 e t sin t ,
x et
t ln x
y1 x cos( ln x), y2 x sin( ln x)
y C1x cos( ln x) C2 x sin( ln x)

65. Пример

Найти общее решение
x 2 y 3xy 13 y 0
y xk
k (k 1) 3k 13 0
k 2 4k 13 0
k1,2 2 3i
y1 x 2 cos(3ln x), y2 x 2 sin(3ln x)
y C1x 2 cos(3ln x) C2 x 2 sin(3ln x)

66. Самостоятельно

1.
x3 y 2 x 2 y xy y 0
2.
x 2 y xy y 0
3.
x 2 y 2 y sin ln x

67. Ответы

1.
k1 1, k2,3 1,
2.
k1,2 i
3.
y
C1
C2 x C3 x ln x
x
y C1 cos(ln x) C2 sin(ln x)
y C1x 2 C2 x 1 0,1cosln x 0,3sin ln x

68. Неоднородные уравнения Эйлера

Найти общее решение x3 y x2 y 2 xy 2 y x3
1. x3 y x2 y 2 xy 2 y 0
y xk
k (k 1)(k 2) k (k 1) 2k 2 0
(k 1)[k (k 2) k 2] 0
(k 1)(k 2 3k 2) 0
k1,2 1, k3 2,
Y C1et C2tet C3e2t Y C1x C2 x ln x C3 x 2

69. Продолжение.

x3 y x2 y 2 xy 2 y x3
Продолжение.
2. В
(k 1)(k 2 3k 2) 0 раскроем скобки:
k 3 4k 2 5k 2 0
По этому характеристическому уравнению составляет левую
часть дифференциального уравнения, а правую часть
t
x
e
получаем из правой части данного заменой
yt 4 yt 5 yt 2 y e3t
y* Ae3t , 3 (совпадений нет)
y* 3 Ae3t , y* 9 Ae3t , y* 27 Ae3t ,
27 Ae3t 4 9 Ae3t 5 3 Ae3t 2 Ae3t e3t
1
4A 1 A
4
1 3t
1 3
*
y e y x
4
4
*

70. Ответ

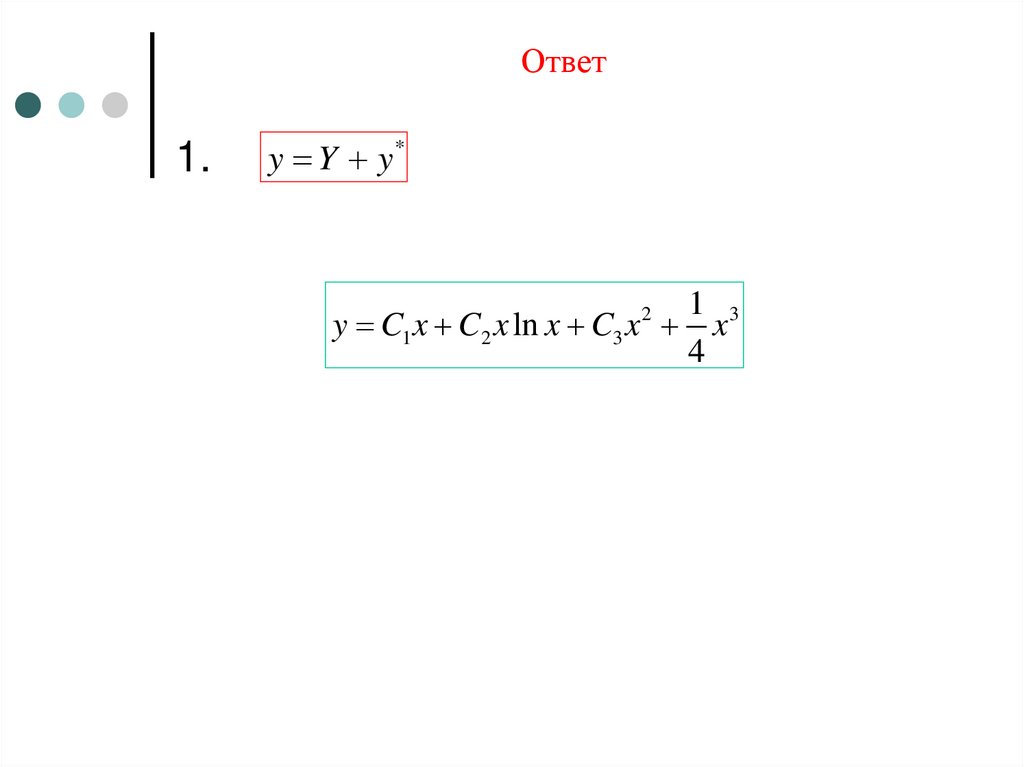
1.
y Y y*
1 3
y C1 x C2 x ln x C3 x x
4
2