Similar presentations:
Графическое решение показательных уравнений и неравенств
1. Графическое решение показательных уравнений и неравенств
Учитель:Санникова Наталья
Владимировна
2.
Функция вида у = аx (a>0), х≠0 называется показательной.Показательная функция бывает двух видов
в зависимости от основания.
Пусть а > 1
а = 2, у =
у
2х
7
1) D(у) = (- ∞; +∞);
у = 2х
6
2) Е(у) = (0; +∞);
5
3) функция не обладает свойством четности и
нечетности;
4
3
4) Функция возрастает на D(у) (- ∞; +∞);
2
5) При х = 0, у = 1 – особая точка!
1
6) х = 0, асимптота графика
7)
-3
х
-3
-1
0
1
2
3
у
1/8 1/4 1/2
1
2
4
8
-2
-2
-1
1
2
3
х
3.
Функция вида у = аx (a>0), х≠0 называется показательной.Показательная функция бывает двух видов
в зависимости от основания.
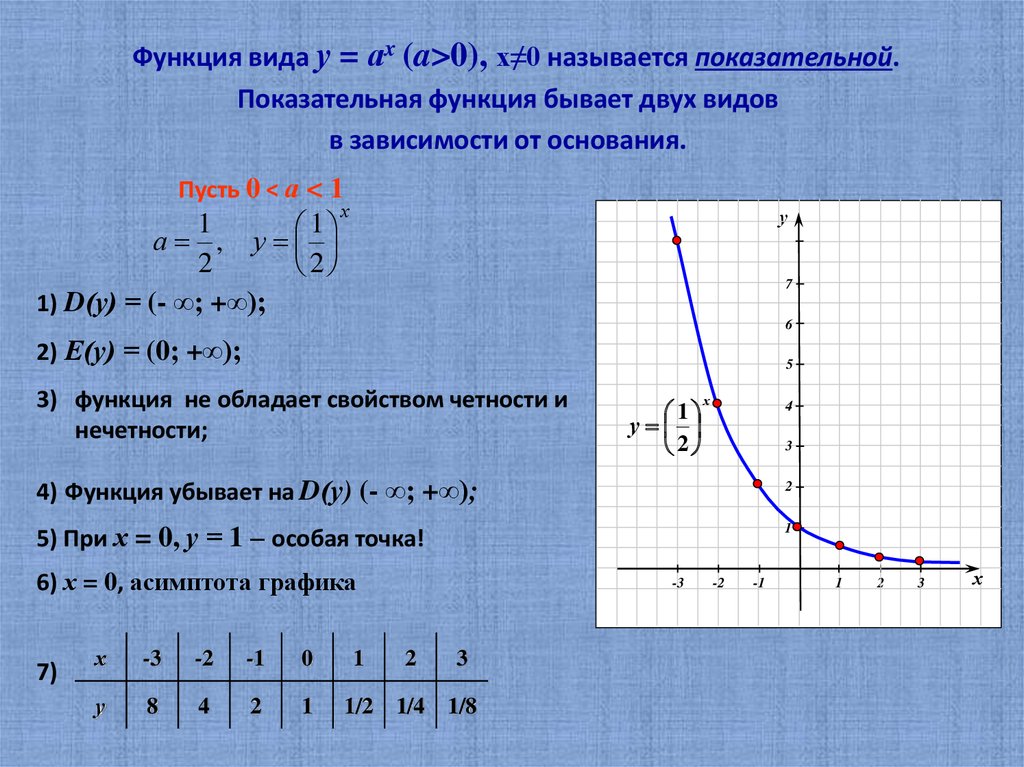
Пусть 0 < а < 1
1
1
а , у
2
2
1) D(у) = (- ∞; +∞);
х
у
7
6
2) Е(у) = (0; +∞);
5
3) функция не обладает свойством четности и
нечетности;
1
у
2
х
4
3
4) Функция убывает на D(у) (- ∞; +∞);
2
5) При х = 0, у = 1 – особая точка!
1
6) х = 0, асимптота графика
7)
х
-3
-2
-1
0
у
8
4
2
1
1
-3
2
3
1/2 1/4 1/8
-2
-1
1
2
3
х
4. Вопросы для зачета
1. График четной функции симметричен относительно2. Запишите функцию, которая является показательной:
y 2 x; y x ; y 2 ; y x
2
x
Область определения показательной функции
Допишите свойство: a x a y
График нечетной функции симметричен относительно
Запишите основание показательной функции
возрастающей на D(у) (- ∞; +∞);
x
y
7. Допишите свойство: a a
8. Асимптота графика показательной функции
9. Область значений показательной функции
x y
10. Допишите свойство: a
11. Запишите основание показательной функции
убывающей на D(у) (- ∞; +∞);
3.
4.
5.
6.
5. Графическое решение уравнений и неравенств
1. 2 х 8Для того чтобы решить уравнение
построим графики функций: y 2 x и y 8
18
16
y 2x
14
12
10
8
6
4
2
0
-5
-4
-3
-2
-1
0
1
2
3
4
5
6.
2 3 1x
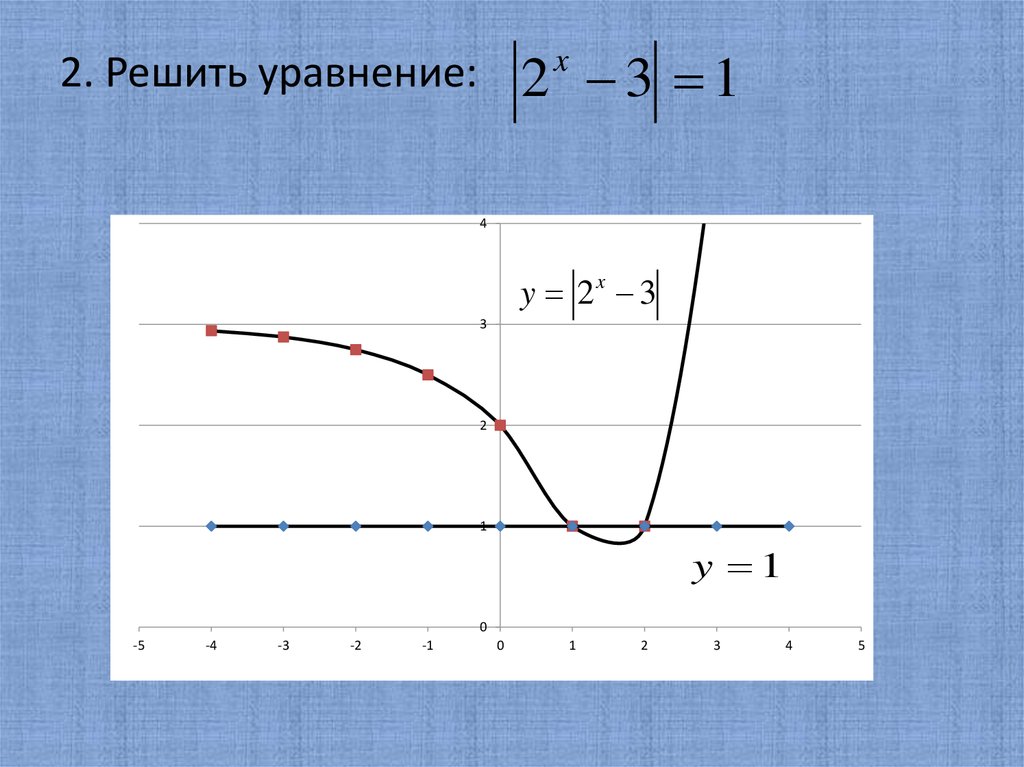
2. Решить уравнение:
4
y 2x 3
3
2
1
y 1
0
-5
-4
-3
-2
-1
0
1
2
3
4
5
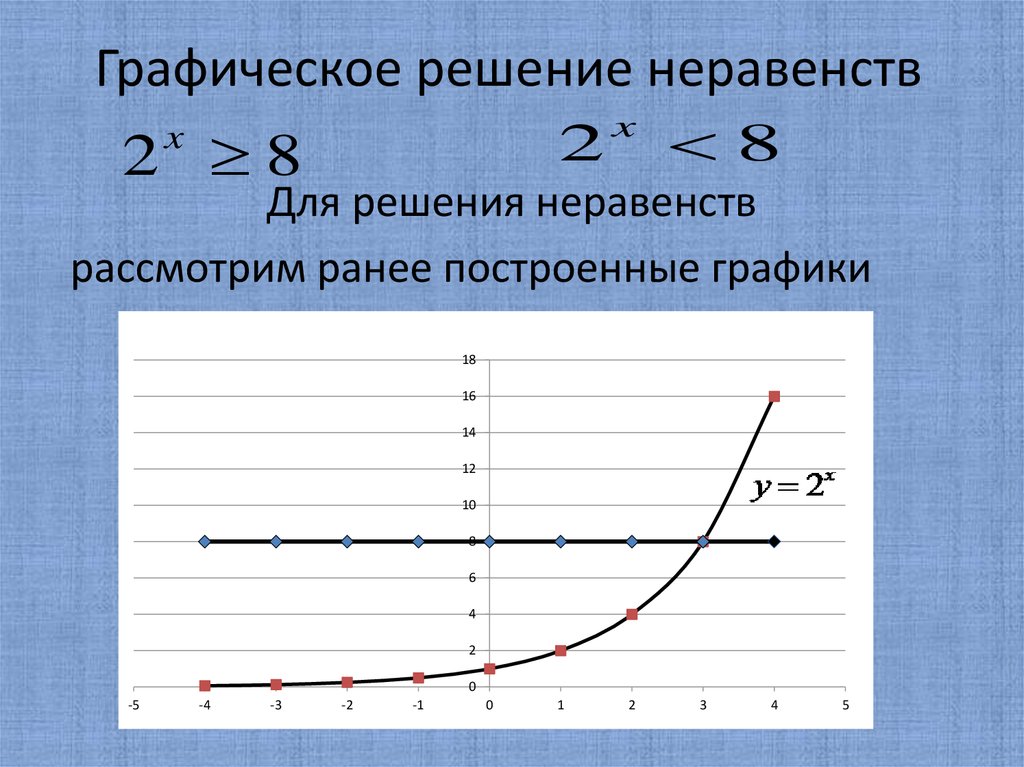
7. Графическое решение неравенств
2 82
x
x
8
Для решения неравенств
рассмотрим ранее построенные графики
18
16
14
12
10
8
6
4
2
0
-5
-4
-3
-2
-1
0
1
2
3
4
5
8.
2 3 12 3 0
x
x
4
3
2
1
0
-5
-4
-3
-2
-1
0
1
2
3
4
5
9. Как решить уравнение графически
1. Построить график правой и левой частиуравнения
2. Найти точки пересечения графиков
3. Если точки есть, то находим координаты
абсцисс точек (х)
4. Записываем ответ
10. Как решить неравенство графически
1. Построить график правой и левой частиуравнения
2. Найти точки пересечения графиков
3. Находим промежутки на оси Ох,
удовлетворяющие условию неравенства
4. Записываем ответ
11. Домашнее задание
№ 200 – решение неравенств№ 197 – определение точек пересечения
графиков








 mathematics
mathematics








