Решение тригонометрических уравнений

1.

Удачи!
sin 4x sin
– sin
2x1 = 0
x
=
cos x = 0

2.

В какой четверти лежит
угол α, если выполняется
условие sinα>0, cosα <0
( Во II)

3.

В какой четверти лежит
угол α, если выполняется
условие sinα < 0, tgα >0
(в III )

4.

Закончите
предложение:
cos(π/2 +α)=…
(-Sinα)

5.

Закончите
(sin2α)
2sinαcosα

6.

Может ли быть верным
равенство
sin²α + cos²α = 3/2 ?
( Нет)

7.

Вычислите
sin²α + tgα∙сtgα + cos²α
(2)

8.

Какие значения может
принимать sinх?
( от -1 до 1 включительно)

9.

Закончите
sin(π-α)=…
(Sinα)
предложение:

10.

Закончите
предложение
cos²α - sin²α =
( cos2α)

11. Формулы решения уравнений sinx =а, cosx = а, tg х=а.

x ( 1) arcsin a k , k Z
k
sinx =а
cosx = а
tg х = а
x arccos a 2 k , k Z
x arctga k , k Z

12.

Вычислите
( π/2)
аrcsin1

13.

Вычислите
( π/2)
аrcсos0

14.

Вычислите
( π/3)
аrctg√3

15.

Вычислите
( π/6)
аrcsin1/2

16.

Вычислите
( 3π/4)
аrccos(-√2/2)

17.

Вычислите
(-π/4)
аrctg(-1)

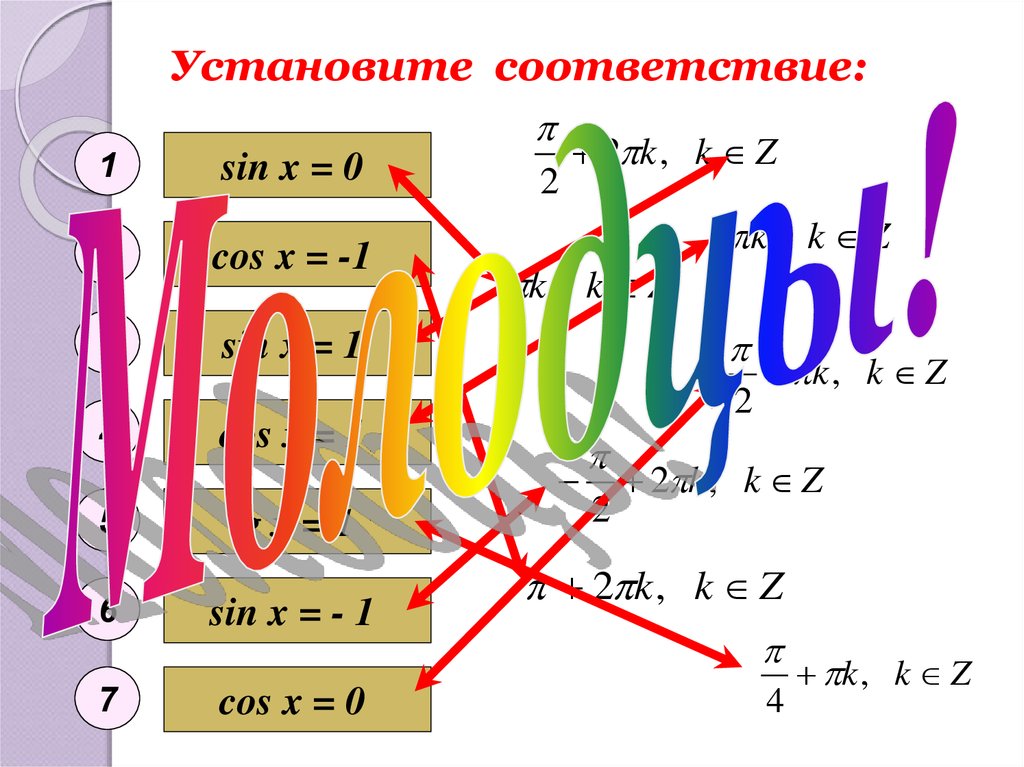
18. Установите соответствие:

1
sin x = 0
2
cos x = -1
3
sin x = 1
4
5
6
7
cos x = 1
tg x = 1
sin x = - 1
cos x = 0
2
2 k , k Z
k , k Z
2 k , k Z
2
2
k , k Z
2 k , k Z
2 k , k Z
4
k , k Z