Решение заданий с параметром. Занятие №1

1.

Решение
заданий с
параметром
Занятие №1

2.

ах +4 = 0
х² - 5х + а = 0
х³ - а = 0
ах ≥ 5
х² + 4а < 0
х + 5а > 0

3.

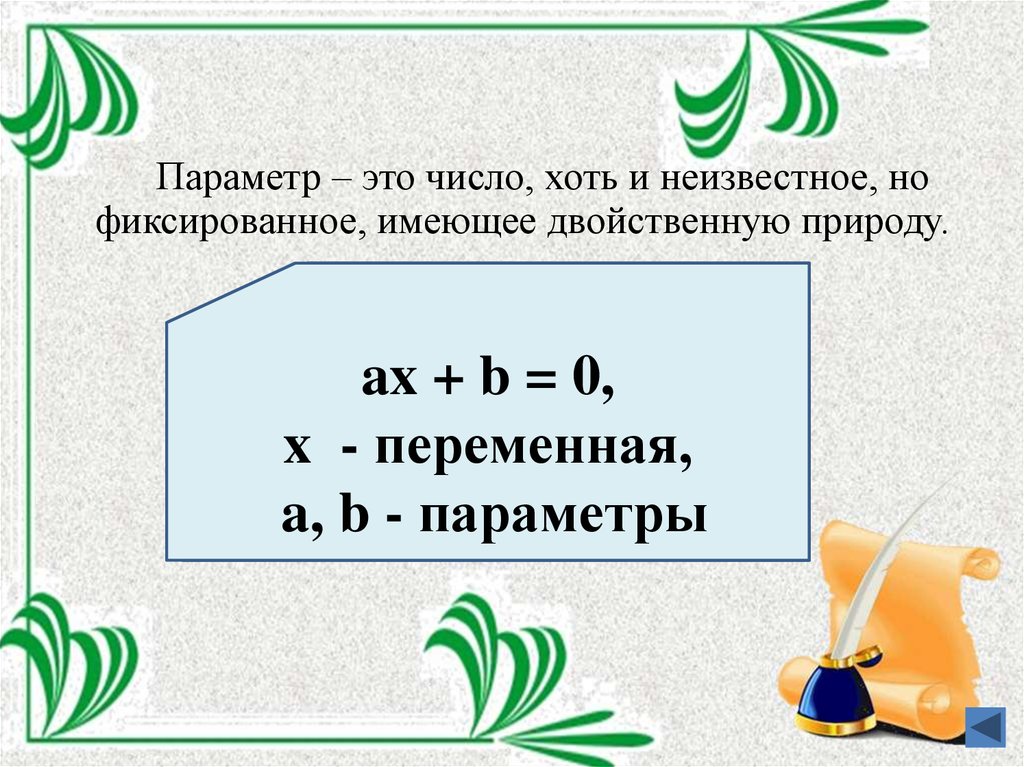
Параметр – это число, хоть и неизвестное, но
фиксированное, имеющее двойственную природу.
ax
ax
y 2=+bx+c=0,
+kx
b =+ 0,
b,
гдегде
xx и-xпеременная,
y- –переменная
переменные,
a,
ka,и
b,bbc,-–-параметры
параметры
параметры

4.

Сравнить –а и 5а
1) если а <0, то –а>0,
5a<0, значит –а>5a
2) если а=0, то –а=0,
5а=0, значит –а=5а
3) если а>0, то –а<0,
5a>0, значит –а<5a.

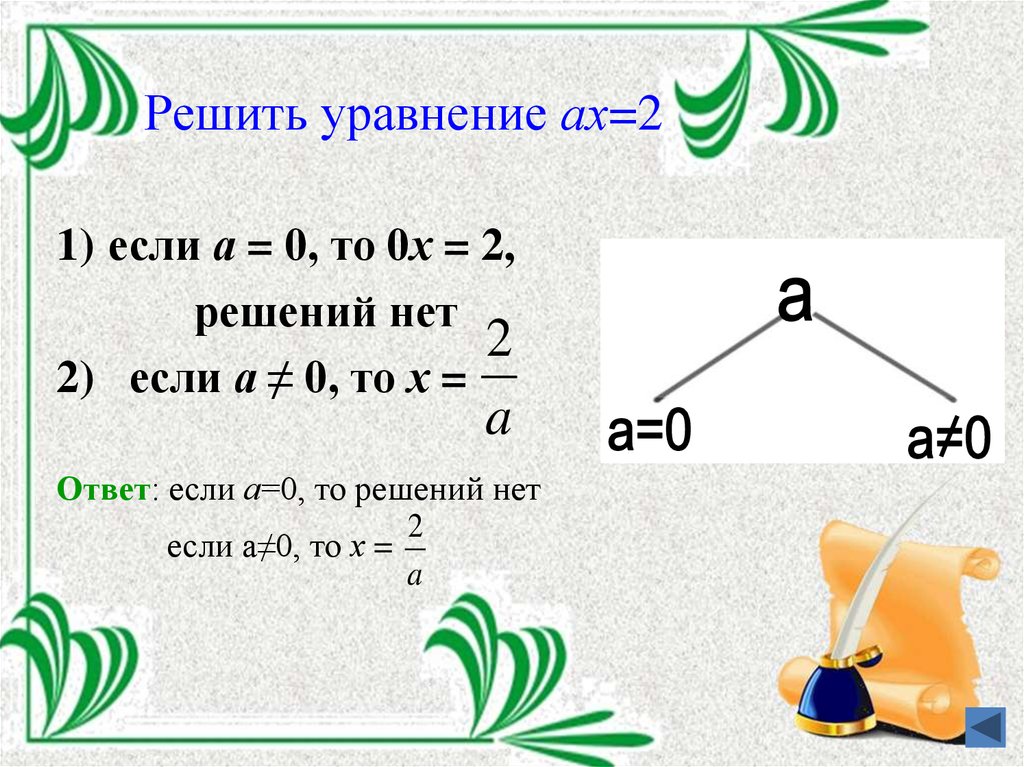
5. Решить уравнение ах=2

1) если а = 0, то 0х = 2,
решений нет
2
2) если а ≠ 0, то х =
a
Ответ: если а=0, то решений нет
2
если а≠0, то х =
a

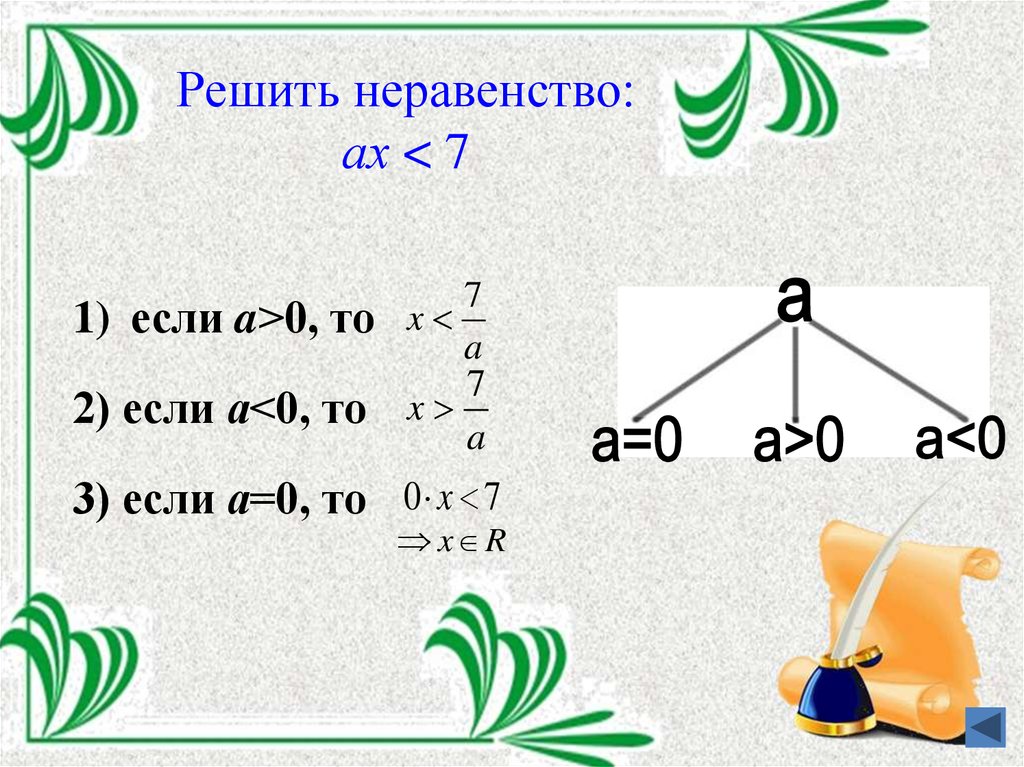
6. Решить неравенство: ах < 7

Решить неравенство:
ах < 7
1) если a>0, то
2) если а<0, то
7
x
a
7
x
a
3) если а=0, то 0 x 7
x R

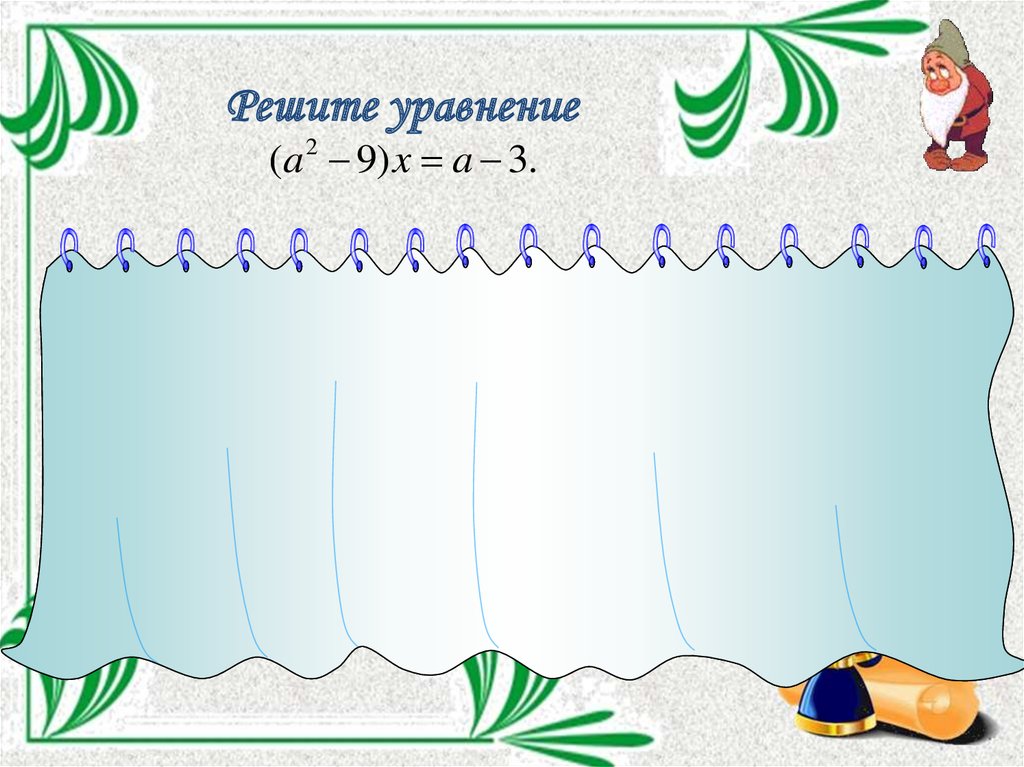
7.

Решите уравнение
(a 2 9) x a 3.
(a 2 9) x a 3
а 3,
1) а 9 0
а 3.
2
При а = 3 0х = 0, х – любое число.
При а = – 3 0х = – 6 – корней нет.
2) При а ±3 х = аа 39 , х = а 1 3 – один корень.
2
1
.
Ответ: при а = 3 х R, при а = -3 корней нет, при а = ±3 х =
а 3

8. Решить уравнение

x a
0
x 3
x a
0
x 3
x a 0,
x a,
x 3 0
x 3.
Ответ: если а = -3, то решений нет
если а ≠ -3, то х = а.

9. Решить уравнение

x b ( x 4) 0
x b 0
x b
x b, b
x b ( x 4) 0 x 4 0, x 4, x 4, b 4.
x b 0
x b
Ответ: если b<-4, то x=-4 или x=b
если b=-4, то x=-4
если b>-4, то x=b.

10.

При каких значениях параметра
а
уравнение ах2–х+3=0 имеет один корень?
ах2–х+3=0
1) При а = 0 – х+3=0 – линейное уравнение.
Следовательно, имеет 1 корень.
2) При а ≠ 0 ах2–х+3=0 – квадратное уравнение.
Следовательно, имеет 1 корень, если D=0.
1
D = 1 – 12а 1– 12а = 0 а = 12 .
1
Ответ: при а = 0, а =
.
12

11.

При каких значениях параметра а
уравнение x 1 1 a не имеет решений ?
x 1 1 a х 1 а 1.
х 1 0 Данное уравнение не имеет решений, если
а 1 0,
а 1.
Ответ: при а < -1.

12.

Умение решать задачи –
практическое искусство, подобное
плаванию, или катанию на лыжах … :
научиться этому можно лишь
подражая избранным образцам и
постоянно тренируясь..
Д. Пойа