Similar presentations:
Линейные уравнения с параметром
1.
Работу подготовилаКоваленко Ирина Анатольевна,
учитель математики школы №3
город Стародуб Брянская область
2.
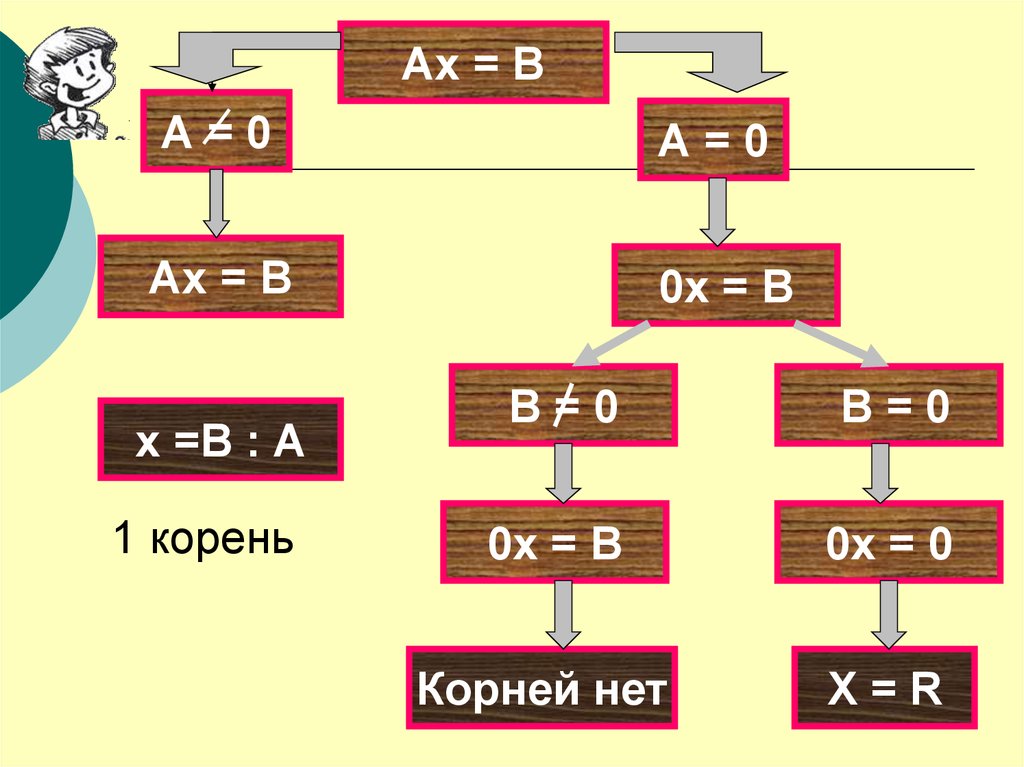
Ах = ВА=0
А=0
Ах = В
0х = В
х =В : А
1 корень
В=0
В=0
0х = В
0х = 0
Корней нет
Х=R
3.
Уравнение с двумя переменными а их вида F(x,a) = 0 называется
уравнением с переменной х и
параметром а, если для любого
значения а надо решить
соответствующие частные уравнения
относительно х
4. Решить уравнение для всех значений параметра а. (а3 -9а)х=а2 – 5а + 6.
Найдем ДЗП: а – любое число.Найдем КЗП:а3-9а=0, а=0, а=-3,
а=3.
Решим соответствующие частные
уравнения для каждого значения
КЗП.
а = 0, то 0х= 6, корней нет;
а= -3, то 0х = 30, корней нет;
а = 3, то 0х =0, х = R
5. Решаем уравнения в общих случаях, т.е.когда а≠0, а≠3, а≠-3
а2 -5а +6Х=
(а -3) (а-2)
=
а3 – 9а
а(а-3) (а+3)
а -2
Х=
а2 + 3а
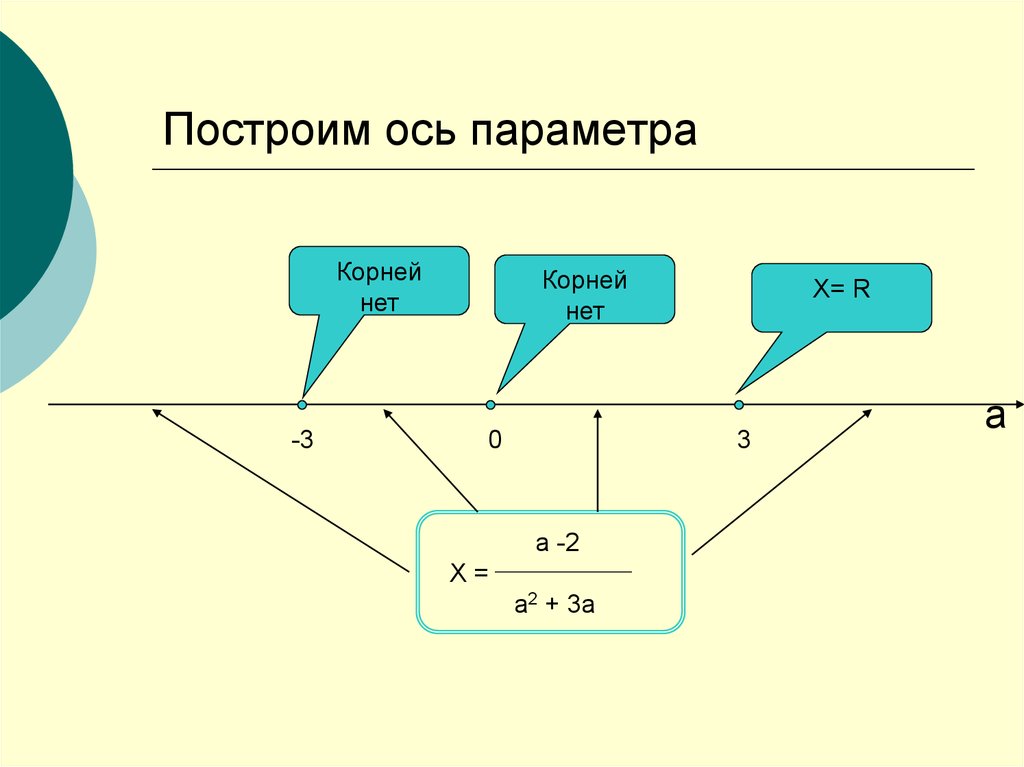
6. Построим ось параметра
Корнейнет
-3
Корней
нет
0
Х= R
3
а -2
Х=
а2 + 3а
а
7. Алгоритм решения линейных уравнений с параметром
Найти ДЗП ( допустимыезначения параметра).
На ДЗП привести уравнение к
стандартному виду.
Найти КЗП и решить частные
уравнения.
Решить общие уравнения.
Нанести все решения на ось параметра.
Записать ответ.
8. Решить уравнения для всех значений параметра .
ах – 4 = 6а – 3х(а-4) (а+7) х = ( а+3) (а – 4)
(с+2)3 х– 2(с+6)(с+2) х=8-8( с+5)






 mathematics
mathematics








