Свойства и график функции y=sinх

1.

2. Цели урока:

• Понятие функции синуса.
Исследование функции (ее свойства).
Уметь строить график функции.
Находить по графику промежутки
возрастания и убывания, промежутки
постоянных знаков, наибольшее и
наименьшее значения функции.

3.

Человека, умеющего наблюдать и анализировать,
обмануть просто невозможно. Его выводы будут
безошибочны, как теорема Пифагора.
А. Конан Дойл

4. Свойства функций

•Область определения функции
•Область значения функции
•Периодичность
•Четность, нечетность
•Нули функции
•Промежутки знакопостоянства
•Промежутки монотонности
•Наибольшее (наименьшее) значение функции

5. Определение синуса.

• Синусом угла называется ордината
точки, полученной поворотом точки
(1; 0) вокруг начала координат на
угол (обозначается

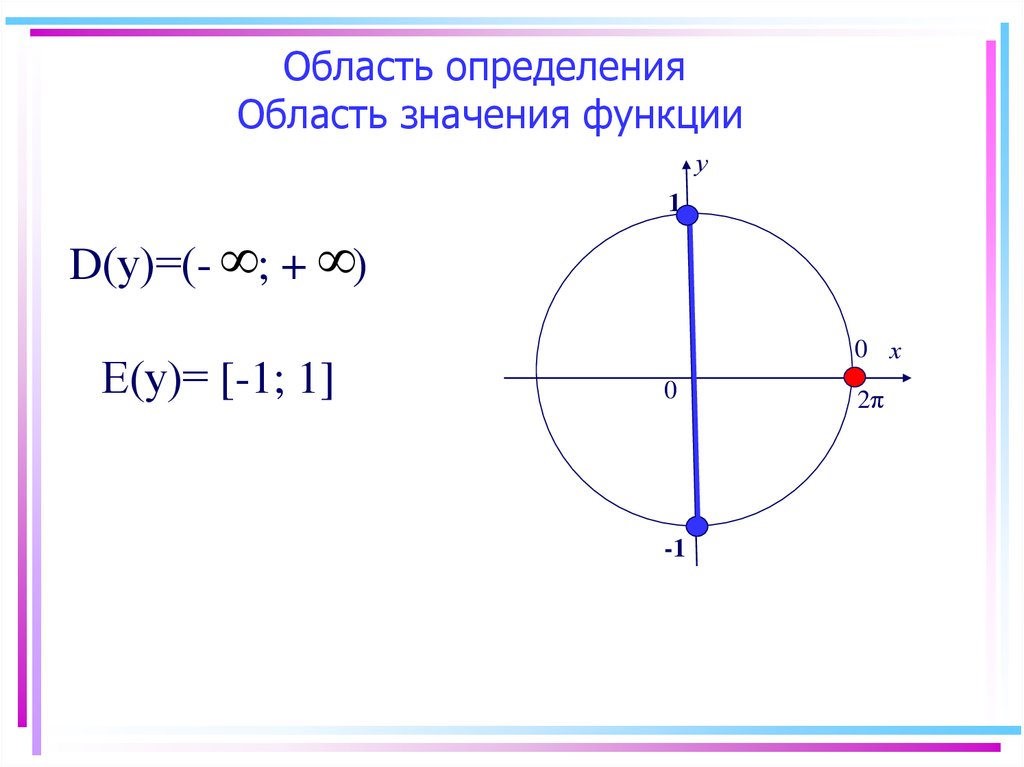
6. Область определения Область значения функции

у
1
D(у)=(- ; + )
Е(у)= [-1; 1]
0 х
0
-1
2π

7. Утверждения для точек числовой окружности

у
I. Определение. sin t = y
2
Синусом числа t называется ордината точки М.
М
у
х
0
-у
3
2
-х
II. Утверждение для точек числовой
окружности: М ( t ) = М ( t + 2 n ), n
0 х
2
III. sin (x +2 n) = sin х, n z
f (х +Т) = f (х –Т) = f (х)
Функция периодическая
IV.sin (-х) = - sin х
f (-х) = - f (х)
Функция
нечетная
z

8. Промежутки монотонности

II
х1 х2
у
π
2
у2
sin х1 sin х 2
М2
у1
III
х1 х2
π
-π
I
х2
0
sin х 1 sin х 2
х1 х2
sin х 1 sin х2
М1
х1
0
х
IV х 1 х 2
sin х 1 sin х 2
3 π
2
-
π
2
Функция возрастает на - /2 + 2 n; /2 + 2 n , Z
n
Функция убывает на /2 + 2 n; 3 /2 + 2 n ,
n Z

9. Свойства функции у = sin х и ее график

D (у) = ( - ; + )
Е (у) = -1; 1
Нули функции: х = n, n Z
у 0 при х ( 2 n; + 2 n), n Z
у 0 при х ( - + 2 n; 2 n), n Z
унаиб. = 1 при х = /2 + 2 n , n Z
унаим. = -1 при х = - /2 + 2 n , n Z
Функция возрастает на - /2 + 2 n; /2 + 2 n , n Z
Функция убывает на /2 + 2 n; 3 /2 + 2 n , n Z
Функция нечетная
Периодическая
Функция непрерывная
y
y = sin x
1
-2π
3π
2
-π
-
π
2
0
-1
π
2
π
3π
2
2π
x

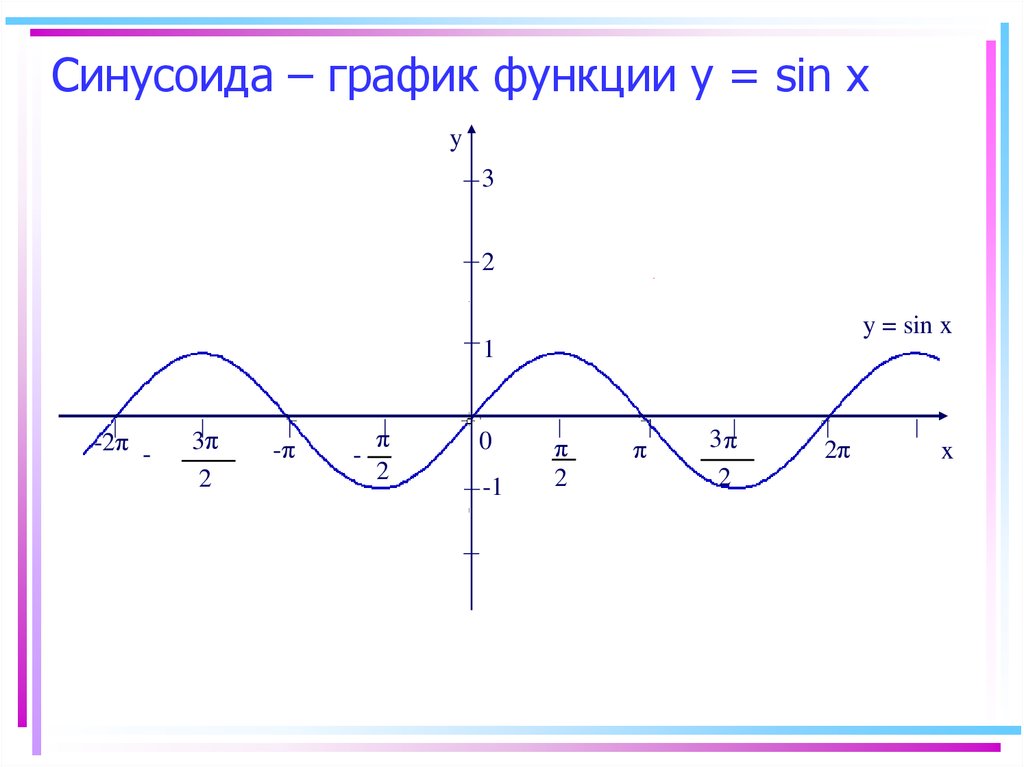
10. Синусоида – график функции у = sin х

y
3
2
y = sin x
1
-2π -
3π
2
-π
-
π
2
0
-1
π
2
π
3π
2
2π
x

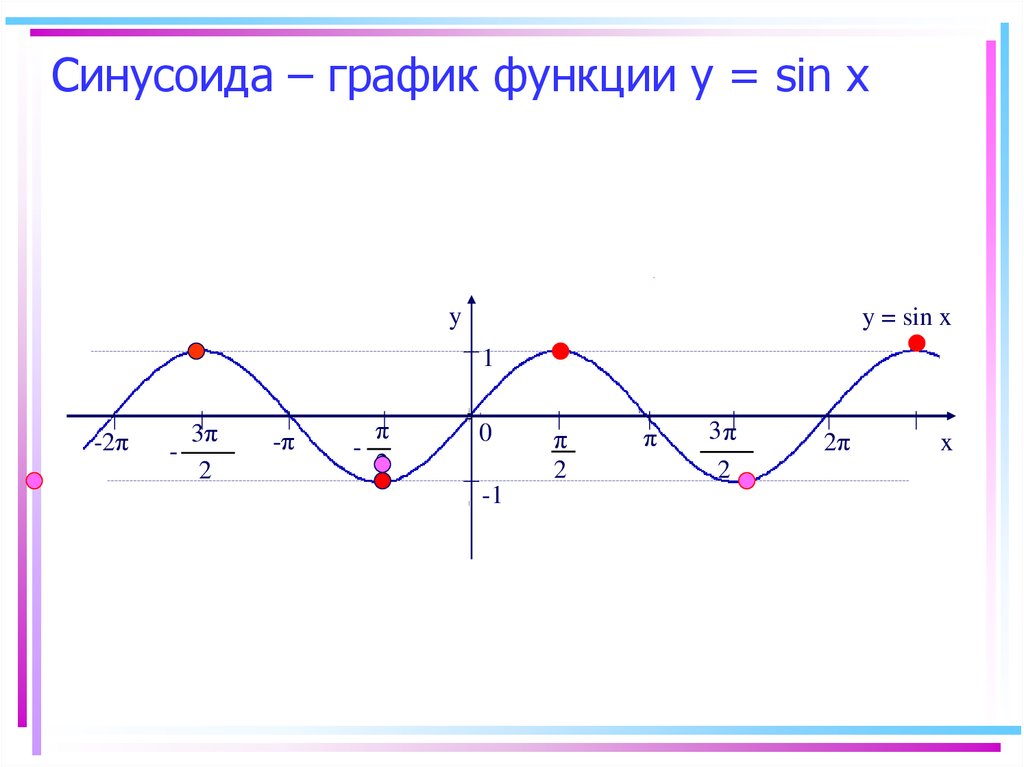
11. Синусоида – график функции у = sin х

y
y = sin x
1
-2π
-
3π
2
-π
-
π
2
0
-1
π
2
π
3π
2
2π
x

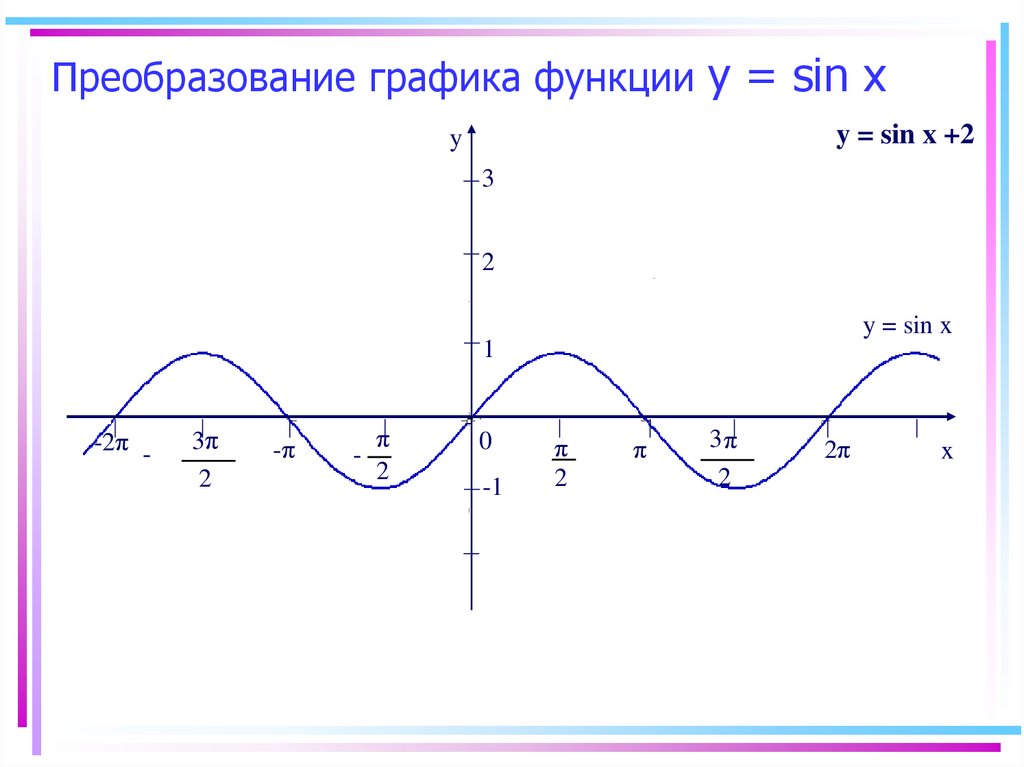
12. Преобразование графика функции y = sin x

y = sin x +2
y
3
2
y = sin x
1
-2π -
3π
2
-π
-
π
2
0
-1
π
2
π
3π
2
2π
x

13.

• Домашнее задание: П 41.
• №722 (2,4); 723 (2,4) №726 (2,4).

14.

Изобразить график функции y = sin x.
на отрезке , перечислить по графику
свойства функции y = sin x.

15. Урок окончен!