Similar presentations:
Тригонометрия. Свойства и график функции y=sin x
1.
Выполнили: Власова Е.А.Тиранова Е.В.
2007г
2. Область определения Область значения функции
у1
D(у)=(- ; + )
Е(у)= [-1; 1]
0 х
0
-1
2π
3. Наибольшее и наименьшее значение функции. Нули функции. Промежутки знакопостоянства.
у π/21
π
-π
0
-1
3π/2 - π/2
y>0
y>0
y<0
y<0
при x = 0 + πn, n z
у=0
0 х унаиб.= 1 при х =
+2 n,n Z
2
2π
унаим.= -1 при х = + 2 n, n Z
2
при 0 < x < π
при х (2πn; π+2πn), n z
при -π < x < 0
при х (-π + 2πn; 2πn), n z
4.
Промежутки монотонностиy
y = sin x
1
-2π
-
3π
2
-π
-
π
2
0
π
2
π
-1
Функция возрастает на - /2 + 2 n; /2 + 2 n
Функция убывает на /2 + 2 n; 3 /2 + 2 n
3π
2
2π
x
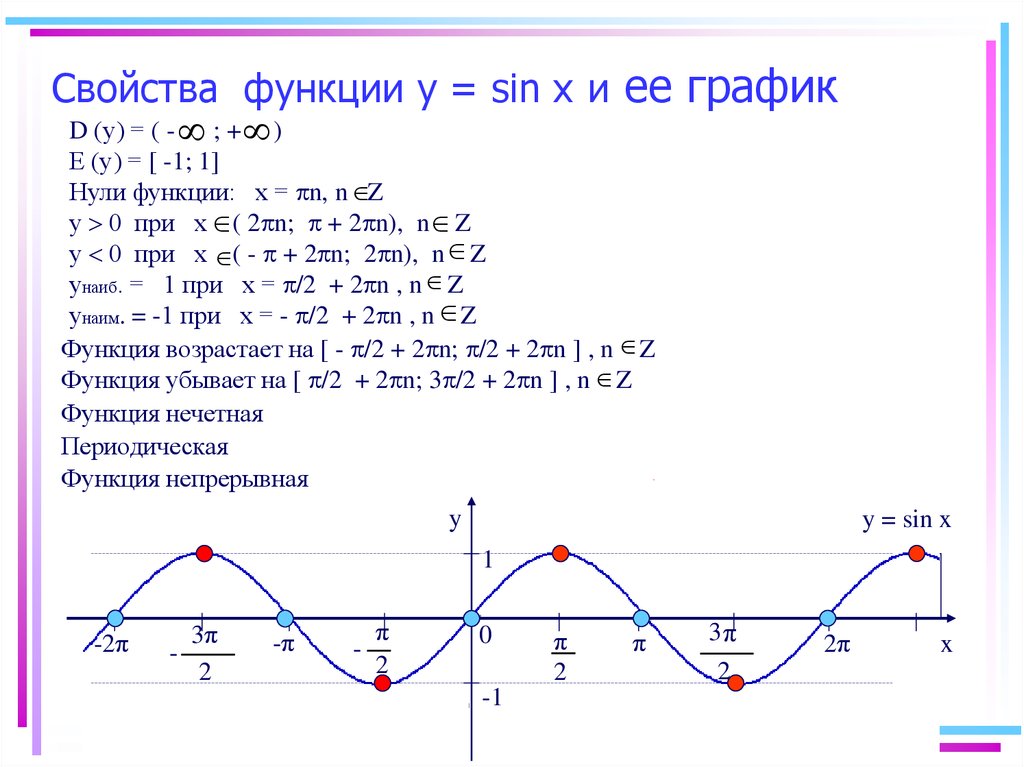
5. Свойства функции у = sin х и ее график
D (у) = ( - ; + )Е (у) = -1; 1
Нули функции: х = n, n Z
у 0 при х ( 2 n; + 2 n), n Z
у 0 при х ( - + 2 n; 2 n), n Z
унаиб. = 1 при х = /2 + 2 n , n Z
унаим. = -1 при х = - /2 + 2 n , n Z
Функция возрастает на - /2 + 2 n; /2 + 2 n , n Z
Функция убывает на /2 + 2 n; 3 /2 + 2 n , n Z
Функция нечетная
Периодическая
Функция непрерывная
y
y = sin x
1
-2π
3π
2
-π
-
π
2
0
-1
π
2
π
3π
2
2π
x
6. График функции y = соs x
Синусоида – график функции у = sin хГрафик функции y = соs x
y
2
y = sin ( x + /2)
1
-2π -
3π
2
-π
-
π
2
0
-1
π
2
π
3π
2
2π
x





 mathematics
mathematics








