Similar presentations:
Приближенное решение дифференциальных уравнений
1. Приближенное решение дифференциальных уравнений
2. Решение ДУ с помощью рядов
• Способпоследовательного
дифференцирования (в виде
ряда Тейлора)
• Способ
неопределенных
коэффициентов
(степенной ряд)
3. Способ последовательного дифференцирования
y f ( x, y, y )y( x0 ) y0
y ( x0 ) y0
y ( x0 )( x x0 ) y ( x0 )( x x0 )
y y ( x0 )
...
1!
2!
(n)
n
y ( x0 )( x x0 )
...
Ряд Тейлора
n!
2
4.
y f ( x, y, y )y( x0 ) y0
y ( x0 ) y0
y ( x0 ) f ( x0 , y0 , y0 ) y0
y ( y ) ( f ( x, y, y )) f1 ( x, y, y , y )
y ( x0 ) f1 ( x0 , y0 , y0 , y0 ) y0
y0 ( x x0 ) y ( x0 )( x x0 ) 2
y ( n) ( x0 )( x x0 ) n
y y0
...
...
1!
2!
n!
5.
y f ( x, y, y )y( x0 ) y0
y ( x0 ) y0
y0 ( x x0 ) y0 ( x x0 )
y y0
1!
2!
(n)
3
n
y0 ( x x0 )
y0 ( x x0 )
...
3!
n!
2
Частичная сумма ряда – приближенное решение
уравнения (частное ).
6. Способ неопределенных коэффициентов
y a1 ( x) y a2 ( x) y f ( x)y( x0 ) y0
y ( x0 ) y0
( x0 R; x0 R)
( x x0 )
y c0 c1 ( x x0 ) c2 ( x x0 ) ...
2
cn ( x x0 ) ...
n
7.
y a1 ( x) y a2 ( x) y f ( x)y( x0 ) y0
y ( x0 ) y0
y c0 c1 ( x x0 ) c2 ( x x0 ) ...
2
y ( x0 ) c0 c1 ( x0 x0 ) c2 ( x0 x0 ) ...
2
c0 y0
y c1 c2 2( x x0 ) c3 3( x x0 ) ...
2
c1 y0
8.
y a1 ( x) y a2 ( x) y f ( x)y( x0 ) y0
y ( x0 ) y0
y y0 y0 ( x x0 ) c2 ( x x0 ) ...
2
y y0 c2 2( x x0 ) c3 3( x x0 ) ...
2
y 2c2 6c3 ( x x0 ) 12( x x0 ) ...
2
( x0 R; x0 R)
9. Метод Эйлера численного интегрирования ДУ
y f ( x, y )y( x0 ) y0
y y (x) – искомая функция (частное решение)
[ x0 ; xn ] X
x X
xn x0
– шаг интегрирования
h
n
х0
y0
х1
y1
х2
y2
…
…
хi
yi
…
…
хn
yn
10.
y f ( x, y )[ x0 ; x1 ]
y y (x)
y( x0 ) y0
M 0 ( x0 ; y0 )
y y ( x0 )( x x0 ) y0
y1 y0 f ( x0 , y0 ) h
[ x1; x2 ]
y y ( x1 )( x x1 ) y1
M1 ( x1; y1 )
y2 y1 f ( x1 , y1 ) h
11.
[ xi 1; xi ]yi yi 1 f ( xi 1 , yi 1 ) h
рекуррентная формула
Точность метода имеет порядок h
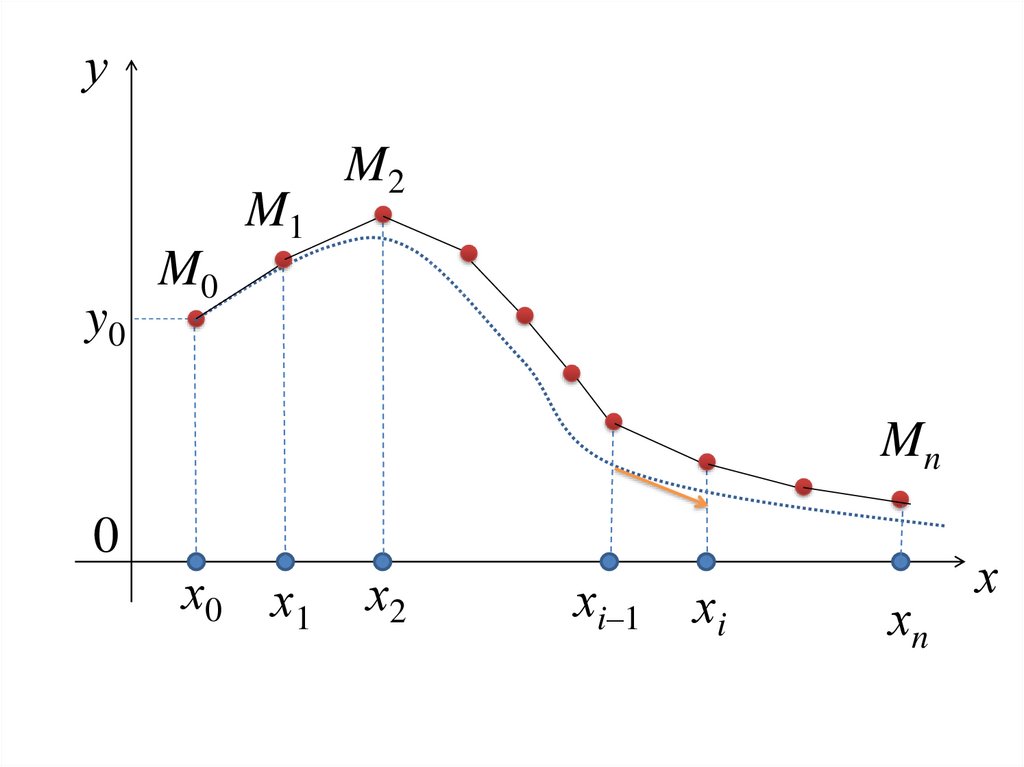
12.
уM1
y0
M2
M0
Mn
0
х0 х1
х2
хi–1
хi
хn
х



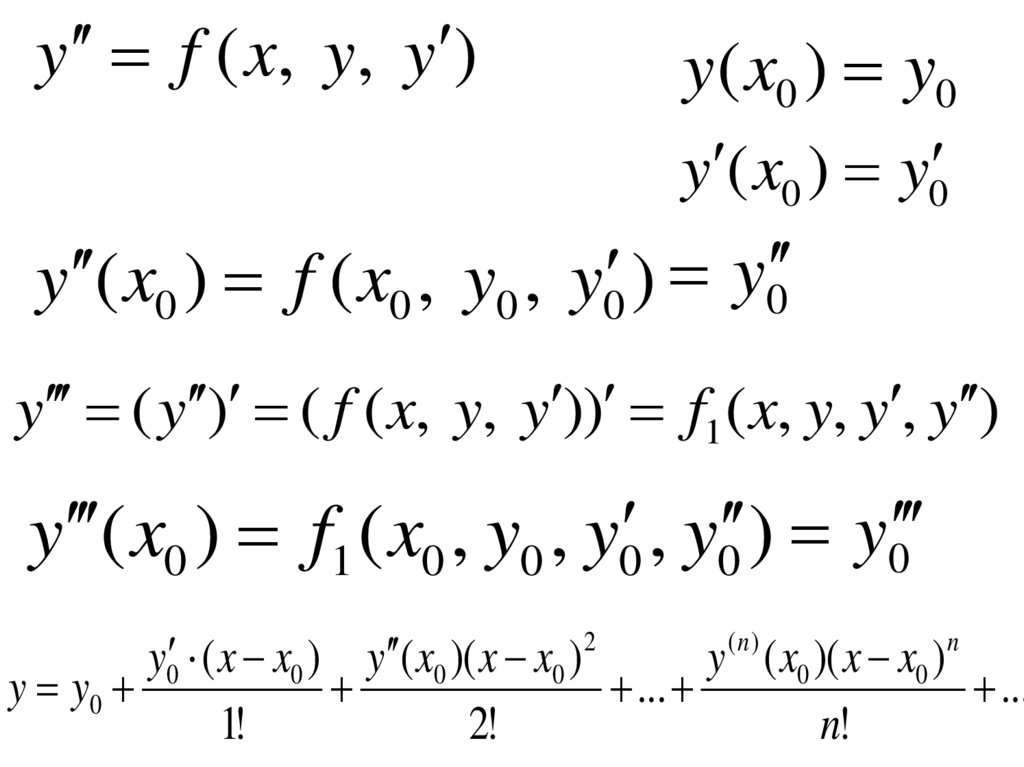


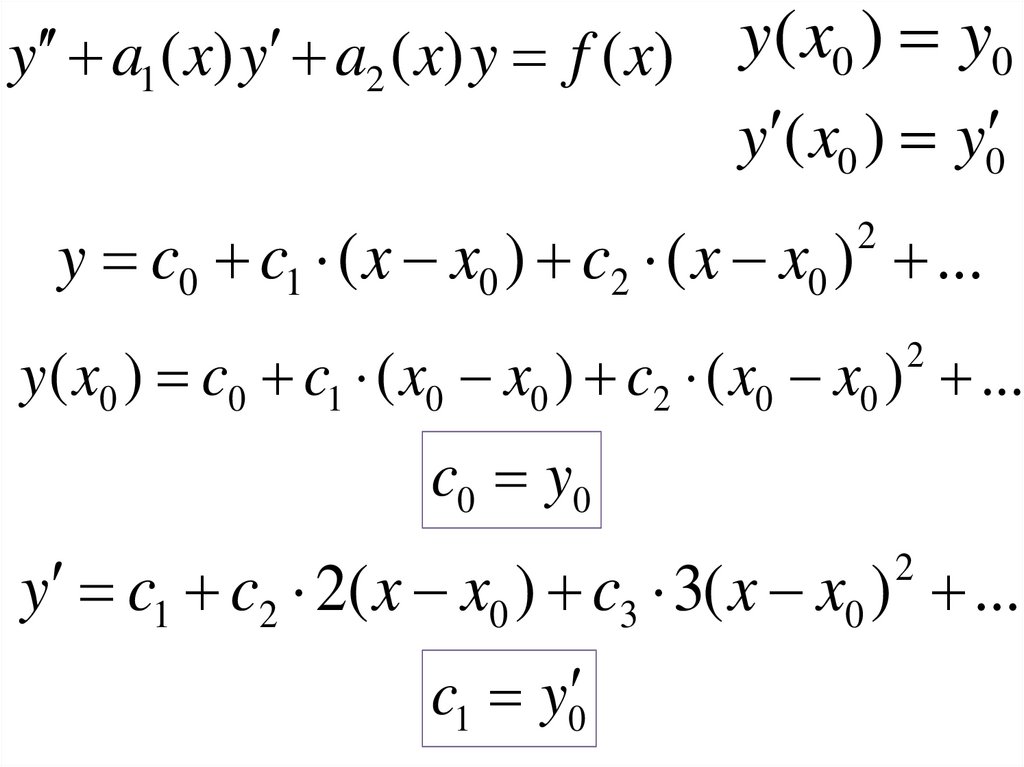


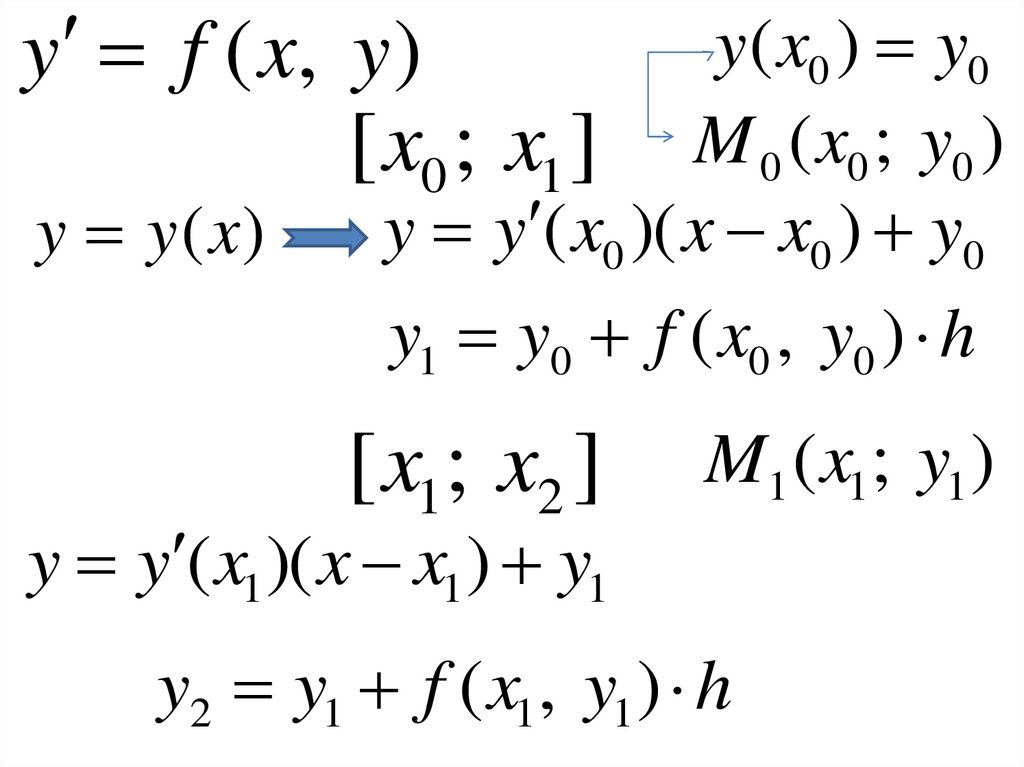

 mathematics
mathematics








