Similar presentations:
Молекулярно-кинетическая теория газов. (Лекция 2)
1.
Курс общей физикиМолекулярная физика и термодинамика
Лекция №2
Молекулярно-кинетическая теория
газов
к.ф.-м.н., доцент ШЕН
Стеблий Максим Евгеньевич
г. Владивосток
2019
2.
Основные выводы МКТСредняя энергия зависит только от температуры и не зависит от массы
молекул.
Отношение универсально газовой постоянной R к числу Авогадро NA,
называется постоянной Больцмана:
R
Дж
k
1,38 10 23
NA
град
Постоянная Больцмана — фундаментальная физическая постоянная,
определяющая связь между температурой и энергией.
Абсолютна температура есть величина, пропорциональная средней
энергии движения одной молекулы.
Заменив в уравнении состояния идеального газа R:
pV kN AT
NA
kT
V
p nkT
p
Если имеется смесь нескольких газов, то давление в этом случае будет
равно:
p nkT n1 n2 ... kT
где n1, n2 – количество молекул первого и второго сорта, содержащееся в
единице объема.
p n1kT n2 kT ... p1 p2 ... pi
Давление – аддитивная величина, скалярная сумма давлений
обусловленных молекулами какого-либо сорта – парциальным
давлением.
VA 22,4 м 3 / моль
1
шт.
моль
Дж
R 8,31
град моль
Дж
k 1,38 10 23
град
N A 6 10 23
Закон Дальтона – давление смеси идеальных газов равно сумме
парциальных давлений газов, образующих смесь.
2
3.
Распределение энергии по степеням свободыВыражение для средней энергии молекул было получено для
одноатомного газа – шариков.
3
2
kT
То есть, учитывалась энергия только поступательного движения молекул.
В более сложных молекулах запас энергии молекул может быть так же
связан с вращательным или колебательным движением.
Число степеней свободы – характеристики движения механической
системы, определяет минимальное количество независимых
переменных, необходимых для полного описания движения
механической системы.
i 3
Теорема о равнораспределении – все движения равновероятны,
поэтому на каждую степень свободы приходится одинаковое количество
энергии.
1
2
Тогда средняя энергия молекулы равна:
i kT
i
2
z
x
y
z
i 5
ϕ
x
y
α
kT
z
i 7
где i – сумма числа поступательных, вращательных и колебательных
степеней свободы молекулы:
i nпост nвращ 2nколеб
y
α
ϕ
x
l
3
4.
ТеплоемкостьA
Можно считать, что в идеальном газе молекулы не взаимодействуют
друг с другом. Тогда внутренняя энергия газа складывается только из
кинетической энергии молекул. Энергия моля газа:
U N A
i
i
N A kT RT
2
2
Для произвольного количества газа:
U
m
U
mi
RT
2
Q
Q
Теплоемкость – величина, равная количеству тепла, которое нужно Если нагревание происходит при постоянном давлении, то газ
сообщить телу, чтобы повысить его температуру на один градус:
будет расширятся, совершая работу. Следовательно, для
повышения температуры потребуется больше тепла, т.к. часть
Q Дж
С
будет уходить на совершение работы. Из первого начала:
dT град
В общем случае величина теплоемкости не является постоянной, а
Q dU pdV
зависит от процесса. Наибольший интерес представляют случаи
постоянного объема и постоянного давления и соответствующие
Получим выражение для теплоемкости:
теплоемкости – Cp и CV
dU
dV
В соответствие с первым началом термодинамики, тепло переданное С p dT p dT
p
системе может идти на совершение работы и/или увеличению
dV
внутренней энергии.
С p СV p
dT p
При постоянном объеме работа не совершается:
Из уравнения состояния идеального газа можно выразить
dU
приращение объема при изменении температуры:
QV dU CV
dT
Подставив:
RT
d
V
d
d i
i
i
p
dT
СV
U
RT R СV R
dT
dT 2
2
2
dV R
Постоянная величина, не зависящая от параметров состояния газа.
dT p
Через теплоемкость можно выразить внутреннюю энергию:
С p СV R
4
U СV T
5.
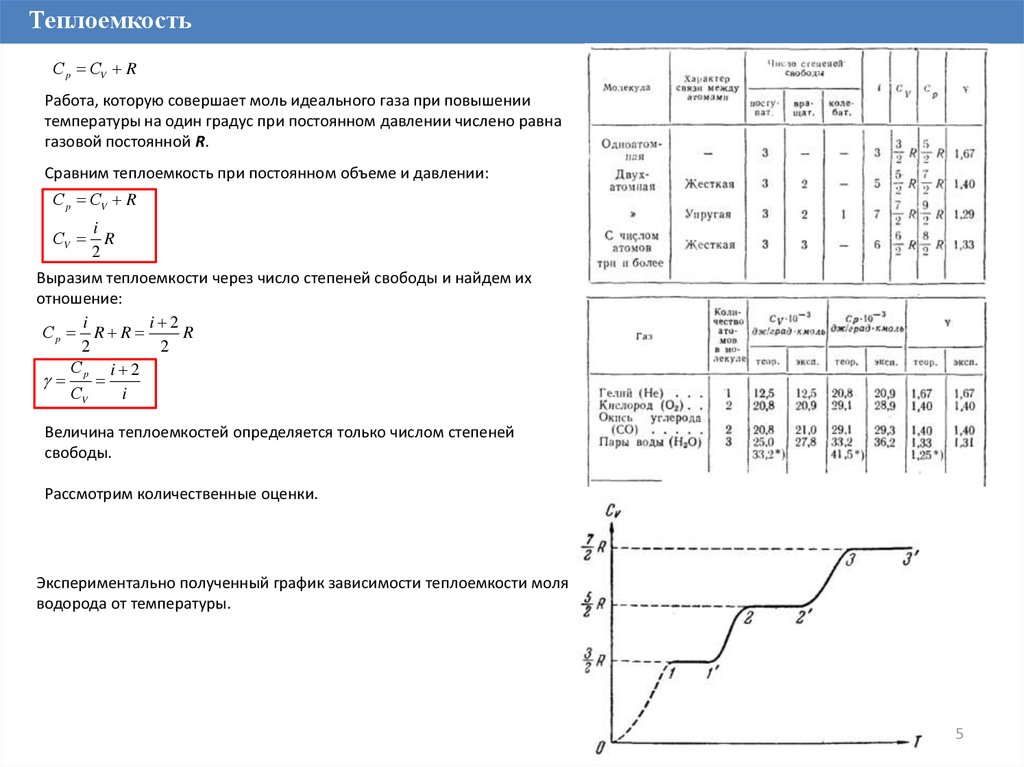
ТеплоемкостьС p СV R
Работа, которую совершает моль идеального газа при повышении
температуры на один градус при постоянном давлении числено равна
газовой постоянной R.
Сравним теплоемкость при постоянном объеме и давлении:
С p СV R
СV
i
R
2
Выразим теплоемкости через число степеней свободы и найдем их
отношение:
i
i 2
Сp R R
R
2
2
С
i 2
p
СV
i
Величина теплоемкостей определяется только числом степеней
свободы.
Рассмотрим количественные оценки.
Экспериментально полученный график зависимости теплоемкости моля
водорода от температуры.
5
6.
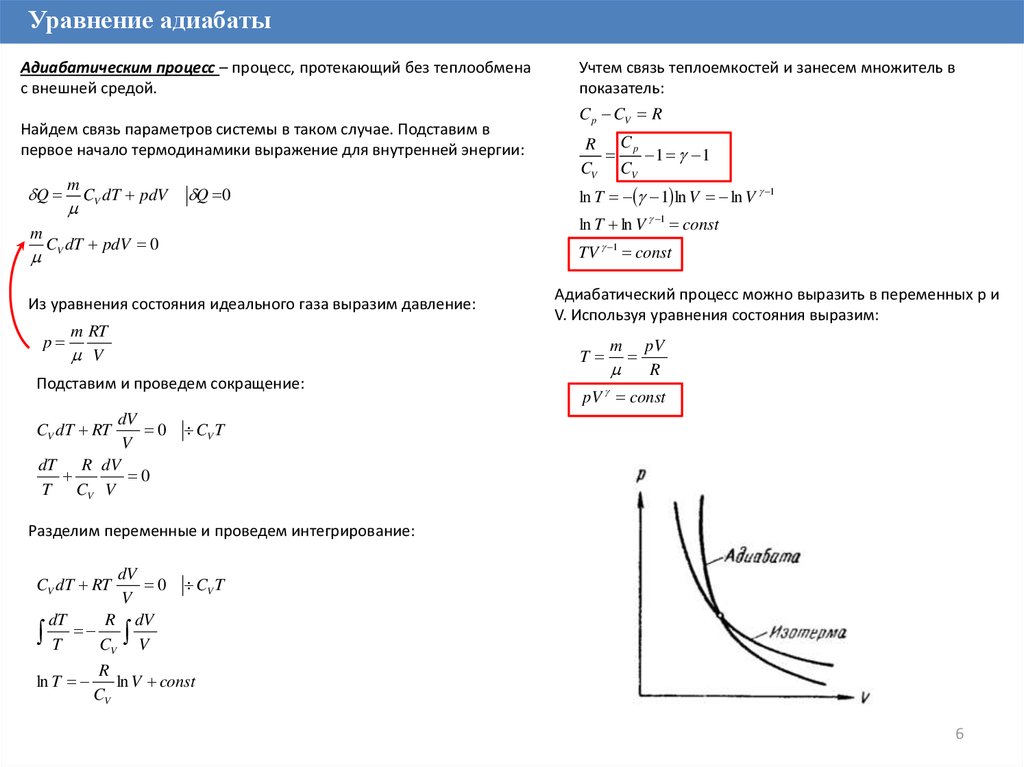
Уравнение адиабатыАдиабатическим процесс – процесс, протекающий без теплообмена
с внешней средой.
Найдем связь параметров системы в таком случае. Подставим в
первое начало термодинамики выражение для внутренней энергии:
Q
m
m
CV dT pdV
Q 0
m RT
V
ln T 1 ln V ln V 1
Адиабатический процесс можно выразить в переменных p и
V. Используя уравнения состояния выразим:
m
T
Подставим и проведем сокращение:
dV
0
V
dT R dV
0
T CV V
R Cp
1 1
CV CV
TV 1 const
Из уравнения состояния идеального газа выразим давление:
CV dT RT
C p CV R
ln T ln V 1 const
CV dT pdV 0
p
Учтем связь теплоемкостей и занесем множитель в
показатель:
pV
R
pV const
CV T
Разделим переменные и проведем интегрирование:
dV
0
V
dT
R dV
T CV V
CV dT RT
ln T
CV T
R
ln V const
CV
6
7.
Политропический процессВсе рассмотренные изопроцессы являются частным случаем политропического
процесса. Процесса, при котором давление и объем связанны соотношением:
pV n const
n – показатель политропы, может принимать любые значения.
При значениях n= 0, 1 и γ уравнение примет вид соответствующий
изобарическому, изотермическому и адиабатическому процессу.
Рассмотрим случай стремления n к бесконечности.
p1V1n p2V2n
Найдем полную производную используя уравнение политропы:
n
p11/ nV1 p12/ nV2
n
V1 V2
Соответствует случаю изохорического процесса.
dV
: TV n 1 const
dT
V n 1dT T (n 1)V n 2 dV 0
dV
V
R
dT
T (n 1)
p (n 1)
Найдем значение теплоемкости при политропическом процессе.
Выразим уравнение политропы в переменных T и V с помощью
nCV C p
R
уравнения состояния идеального газа:
C CV
T
(n 1)
n 1
pV n const p R
V
Полученное выражение не содержит параметров состояния
n 1
TV const
p, V или T, то есть теплоемкость есть величина постоянная.
Используя первое начало термодинамики и определение
теплоемкости:
Политропный процесс — термодинамический процесс, во
время которого теплоёмкость газа остаётся неизменной.
Q CV dT pdV
C
Q
dT
CV p
dV
dT
n
Cp C
CV C
7
8.
Работа идеального газаРанее была найдено выражение для работы при переменном объеме.
Найдем величину работы в произвольном процессе используя
определение политропного процесса.
В общем виде работа газа при переходе из состояния 1 в состояние 2
определяется формулой:
V2
A12 pdV
Вычислим работу при изотермическом процессе:
A12
V2
pdV
V1
A12
m
A12
m
V1
Что бы произвести интегрирование необходимо выразить давление
через объем:
V2
dV m
V
RT ln 2
V
V1
V1
RT
RT ln
V2
V1
pV n p1V1n p2V2n
Где индексы 1 и 2 соответствуют начальному и конечному состоянию, а
отсутствие индексу – произвольному состоянию между ними. Выразим
давление и подставим в общий интеграл.
p
Работа при изобарическом процессе:
A12 p V2 V1
p1V1n
Vn
A12 p V
n
1 1
V2
dV
V
n
V1
Рассмотрим случай n≠1
V2
dV
V
V1
n
1 1
1
n 1 n 1
n 1 V1
V2
n 1
p1V1 V1
1
A12
n 1 V2
Преобразуем уравнение используя уравнение состояния идеального
газа:
m
p1V1 RT1
n 1
m RT1 V1
1
A12
n 1 V2
8
9.
Распределение Максвелла (выводы)p
2kT
m
Наиболее вероятная скорость
8kT
m
Средняя скорость
2
3kT
m
Среднеквадратичная скорость
9







 physics
physics








