Similar presentations:
Основные законы магнитного поля: теорема Гаусса и теорема о циркуляции индукции магнитного поля
1.
§21 Основные законы магнитногополя: теорема Гаусса и теорема о
циркуляции индукции магнитного
поля
Глава 3
Электричество и магнетизм
2.
Для магнитного поля, как и для электрического,необходимо установить две важнейших теоремы:
теорему Гаусса (поток вектора В сквозь замкнутую
поверхность) и теорему о циркуляции вектора В по
замкнутому контуру.
3.
Линии магнитного поля замкнуты сами на себя иохватывают ток. Поэтому, очевидно, поток вектора В
сквозь любую замкнутую поверхность будет равен
нулю.
B
d
S
0
S
4.
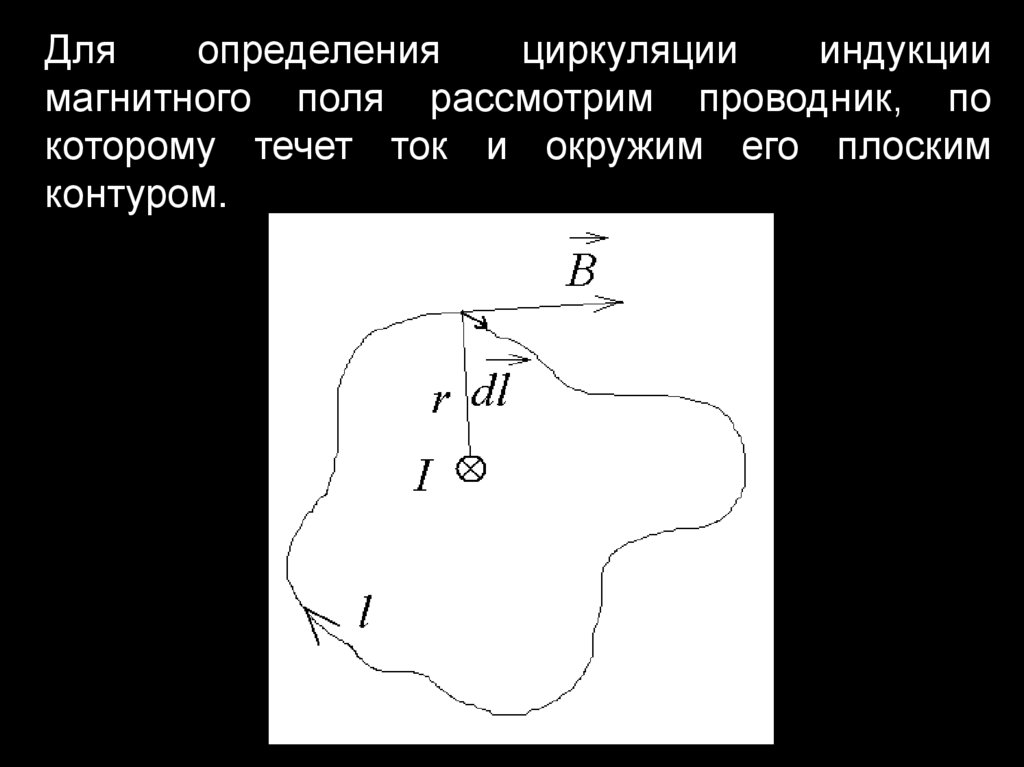
Дляопределения
циркуляции
индукции
магнитного поля рассмотрим проводник, по
которому течет ток и окружим его плоским
контуром.
5.
Циркуляция вектора индукции равна:0 I
Bdl B cos dl 2 r cos dl
l
l
l
0 I
0 I
rd
2 0 I
2
l 2 r
6.
Циркуляция вектора магнитной индукции позамкнутому контуру пропорциональная току,
охватываемому контуром:
B
d
l
I
0
l
7.
Согласно принципу суперпозицииB Bi
B
d
l
I
0
i
l
i
Циркуляция вектора магнитной индукции по
замкнутому контуру равна алгебраической
сумме
токов,
охватываемых
контуром,
умноженной на 0.
8.
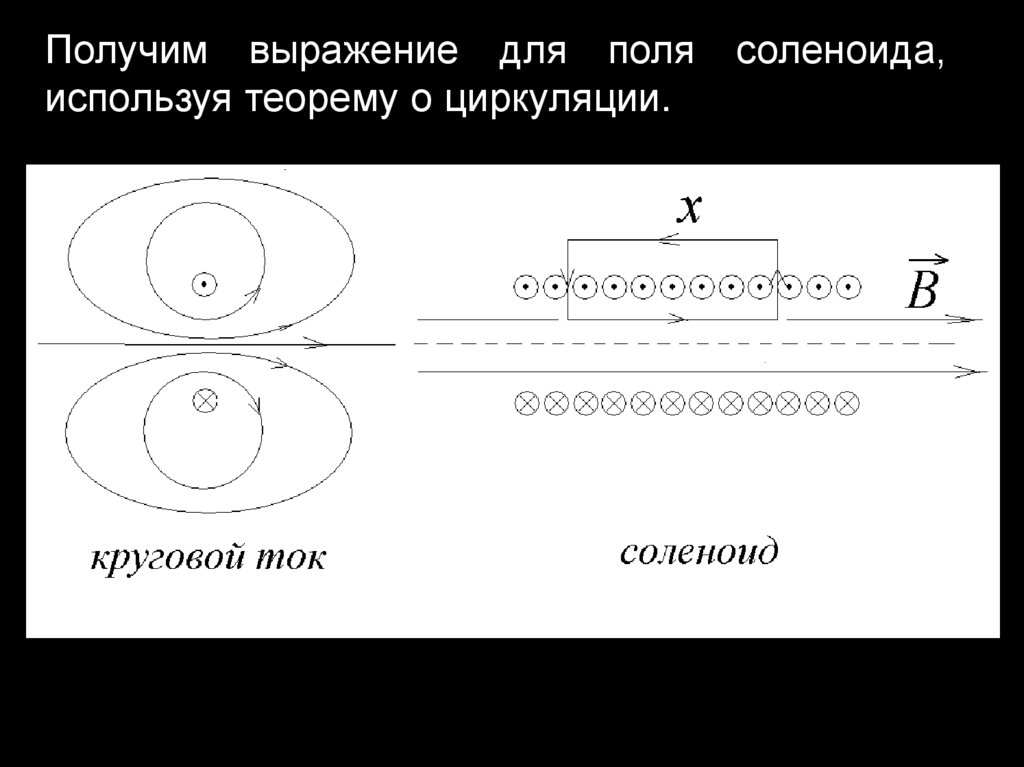
Получим выражение для поляиспользуя теорему о циркуляции.
соленоида,
9.
Циркуляция определяется слагаемым вдольконтура внутри катушки.
Bdl Bx
l
Bx 0 NI
N
B 0 I 0 nI
x
Плотность числа витков:
N
n
x
10.
Поле внутри катушки (соленоида) однородное:B 0 nI
11.
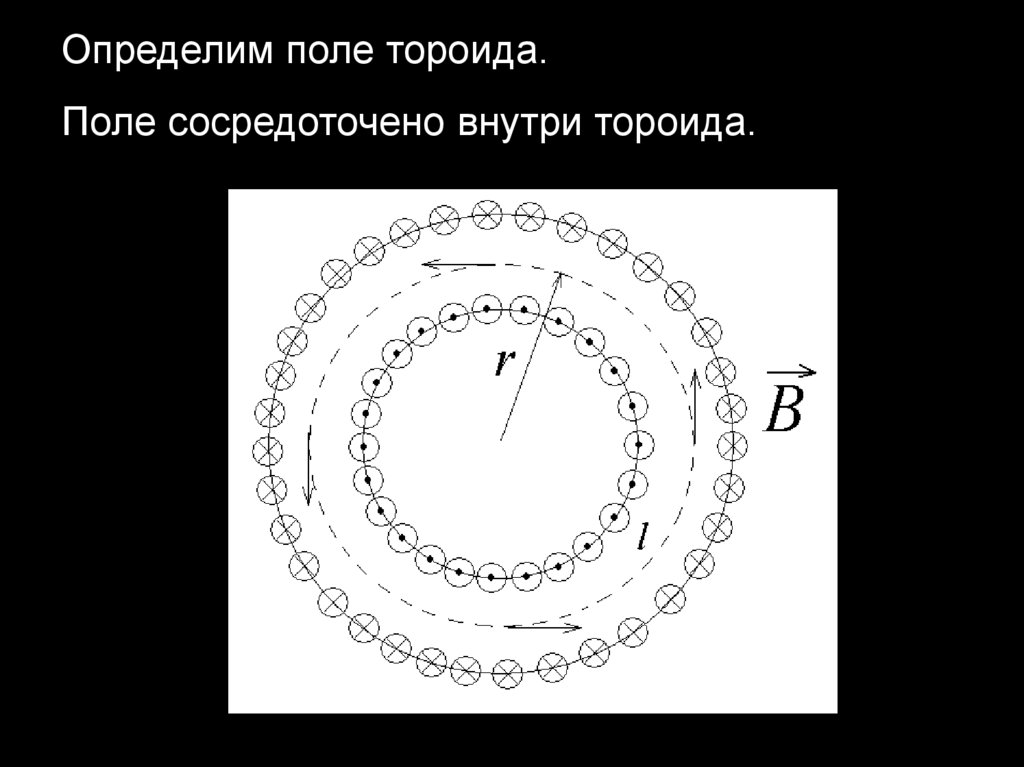
Определим поле тороида.Поле сосредоточено внутри тороида.
12.
Циркуляция вектора индукции по замкнутомуконтуру:
B
d
l
2
rB
l
2 rB NI 0
Поле внутри тороида не однородное и
уменьшается к краю катушки:
0 NI
B0
2 r









 physics
physics








