Similar presentations:
Применение компьютерных технологий в изучении математики
1. «Применение компьютерных технологий в изучении математики»
Подготовилаучитель математики
«МОУ Авсюнинская СОШ»:
Шишкова Валентина Валерьевна
2.
В качестве объекта исследования выступаетучебные занятия по алгебре в 11 классах.
Предметом исследования является
обучение школьников алгебре и подготовка к
сдаче ЕГЭ с помощью компьютерных
технологий в рамках учебных занятий со
школьниками 11 классов.
Основной целью данной работы является
отбор содержания и методом обучение
школьников в рамках учебного процесса по
алгебре и подготовка к сдаче ЕГЭ по
математике с помощью компьютера.
3.
2. Педагогические цели, решаемые с помощью компьютера.быстрое решение вычислительных задач, трудоемкое для
ручного выполнения;
проведение уроков с динамичными демонстрационными
программами - повышение наглядности учебного процесса;
повторение и закрепление вопросов математики с помощью
программных тренажёров - обеспечение обратной связи в
процессе обучения;
разработка генераторов индивидуальных заданий;
использование обучающих программ по математике интерактивное обучение учащихся в диалоге с компьютером.
руководство научными исследованиями учащихся организация коллективной и групповой работы;
разработка педагогических программных средств;
индивидуальные консультации учащимся - обеспечение
индивидуализации учебного процесса;
протоколирование и правка карты знаний учащихся.
подготовка к ЕГЭ по математики.
4.
3. Применением информационныхтехнологий в11 классе.
Тема: « Показательное уравнение»
Цели :
1. Проверка знаний основных теоретических вопросов по теме
“Показательная функция” и подготовка к сдаче ЕГЭ с помощью
компьютера.
2. Введение понятия “показательное уравнение”.
3. Формирование навыков решения простейших показательных
уравнений.
4. Графический способ решения уравнений.
5. Воспитание познавательного интереса к математике .
6. Воспитание наблюдательности, самостоятельности, способности к
коллективной работе.
5.
Оборудование:Компьютерный класс, проектор,
компьютерные программы “Графики”,
« MyTest2-4», презентация урока в
программе PowerPoint.
6. Устная работа. Показ через проектор.
Представить данную функциюв виде показательной Y=Аx
1. Y=3x ·4x
Y=12x
2. Y=6x:2x
Y=3x
3. Y=52x
Y=25x
4. Y=43x :25x
Y=26x :25x
Y=2x
7. Первая группа садится за компьютеры и проходит тестирование по теме “Показательная функция” при помощи теста, составленного в
программе «MyTest2-4»8.
Вторая группа за партами.Найдите возможную закономерность
последовательности
:
9.
Тема :“Показательные уравнения и решения
простейших из них”.
10. Как решить уравнения вида:
2х=4х;3х=х2 ?
11.
4. Графический способ решенияуравнений.
Итак, для того, чтобы решить уравнение
графически, надо найти абсциссы точек
пересечения графиков функций обеих
частей уравнения.
12. Работа с графикой на ПК.. - Ребята, используя программу “Графики”, решают графически простейшие уравнения. А) 2х=4; 2х=0;
2х=-1.В) 0,5х=1; 0,5х=4; 0,5х=-1;
13.
14.
15.
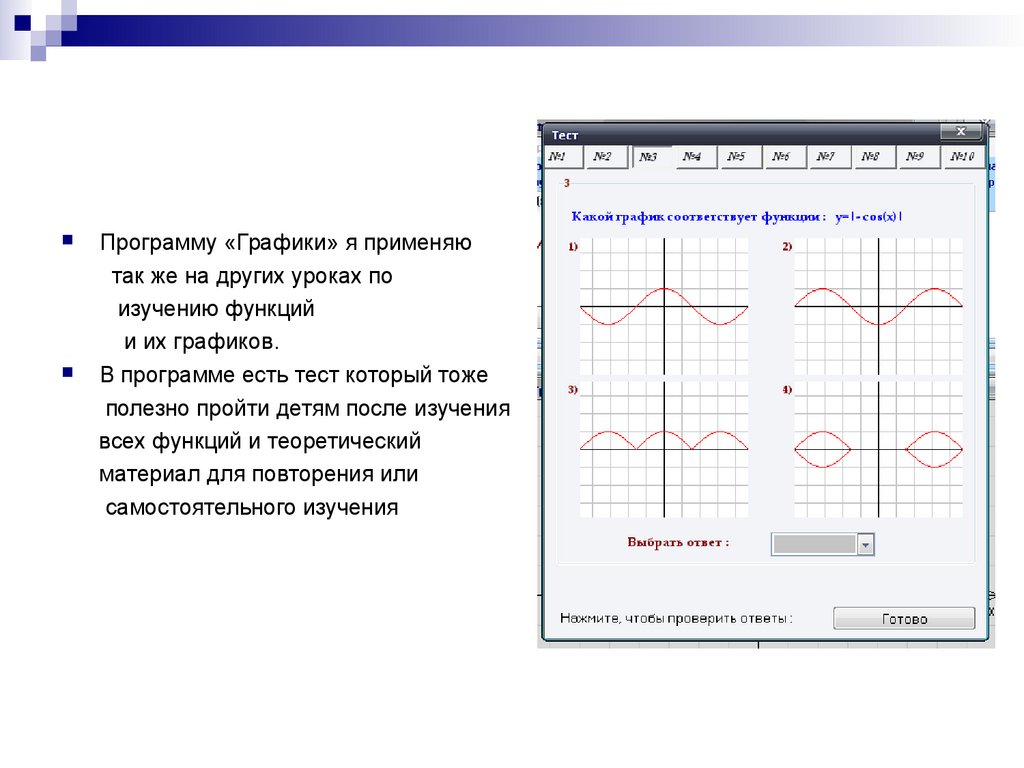
Программу «Графики» я применяютак же на других уроках по
изучению функций
и их графиков.
В программе есть тест который тоже
полезно пройти детям после изучения
всех функций и теоретический
материал для повторения или
самостоятельного изучения
16. Программированный контроль через проектор (за 7 минут до конца урока). Выбрать правильный ответ
уравнения1
2
3
4
4х =64
2
2
4
3
нет
решения
4
нет
3решения
1/3
1/3
(1/2)х =1/32
4
4
5
-5
3
3
-4 -4
-5 5
5х-1 =5
0
0
2
2
5
5
-1 -1
11
3*3х =9
1
1
2
2
3
3
1/2
1/2
00
7х =-7
1
1
нет
решения
-1
нет
-1
0
решения
5
0
77
17.
Обучающая презентация,подготовленная для ученика,
пропустившего урок.
18.
Для детей пропустивших темы можнопредложить изучить их с помощью
видео уроков.
19.
20.
21.
22.
В геометрии я применяю программу видеопостроения, для наглядности и экономии
времени:
Эта программа особенно удобна для
самостоятельного изучения тем на
построение с помощью циркуля и линейки
23.
Кроме описанной технологии примененияпрограммного обеспечения, на уроках математики
возможно применение специализированных
программ, таких как "Живая Геометрия", "Курс
математики 98" фирмы Компьюлинк, "Живая
математика" фирмы Физикон, " GeoGebra"
"Репетитор по математике" фирмы Кирилл и
Мефодий. Применение таких программных продуктов
позволяет визуализировать и сделать более
наглядными многие математические понятия и
абстракции, позволяют развивать пространственное
воображение, организовывать контроль знаний. При
применении их наряду с традиционными формами
работы на уроке позволяют получать хорошие
педагогические результаты .
24.
Примеры тем уроков на которыхприменяю компьютер.
Пример 1. Для решения задач по стереометрии
необходимо владеть пространственным
воображением и удачно выбирать изображение.
Программа GeoGebra позволяет “поворачивать” тело
так, чтобы необходимое сечение оказывалось в
плоскости экрана, т.е. помогает стереометрическую
задачу свести к циклу планиметрических, способы
решения которых стандартны.
25.
Пример 1. Учебное исследованиеквадратичной функции ученик может
проводить самостоятельно и успешно с
помощью компьютера. Приведя
первоначальную форму y = ax2 + bx + c
к виду y = p(kx + l)2 + q, ученик без
особого труда найдет функциональную
зависимость графика от параметров k,
l, p, q.
26. Презентации некоторых тем по математики
27. Тригонометрические уравнения
Вопросы для повторения:уравнение cost = a
уравнение sint = a
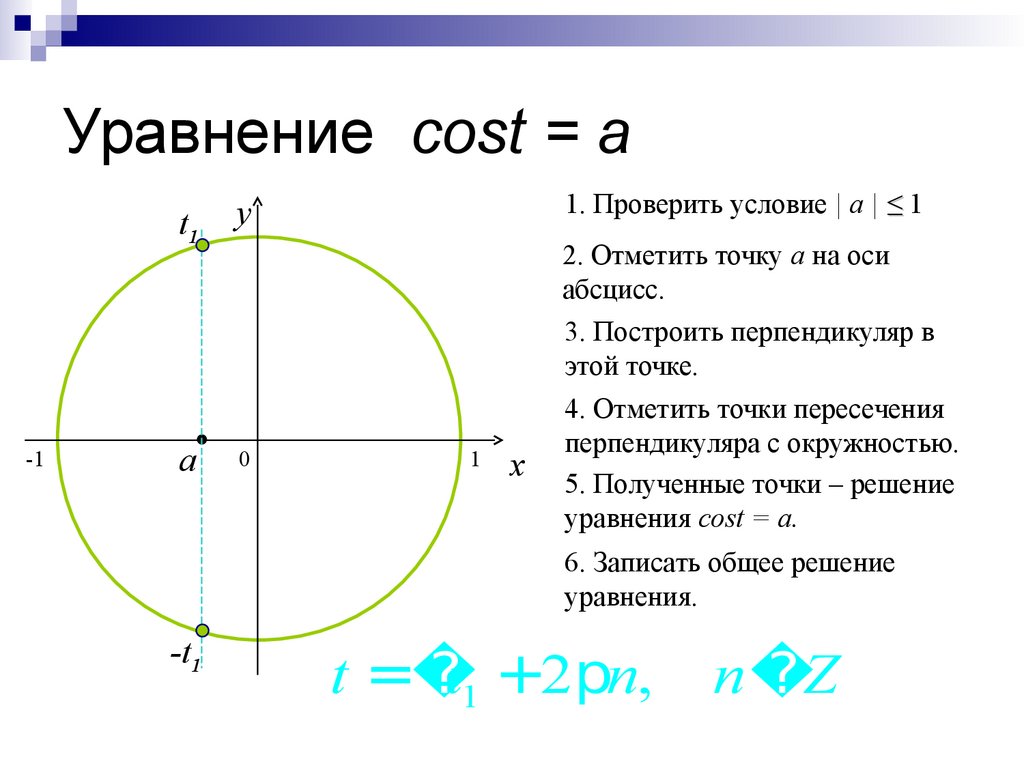
28. Уравнение cost = a
-1t1
y
a
0
1. Проверить условие | a | ≤ 1
1
x
2. Отметить точку а на оси
абсцисс.
3. Построить перпендикуляр в
этой точке.
4. Отметить точки пересечения
перпендикуляра с окружностью.
5. Полученные точки – решение
уравнения cost = a.
6. Записать общее решение
уравнения.
-t1
t =
t1 +2pn,
n Z
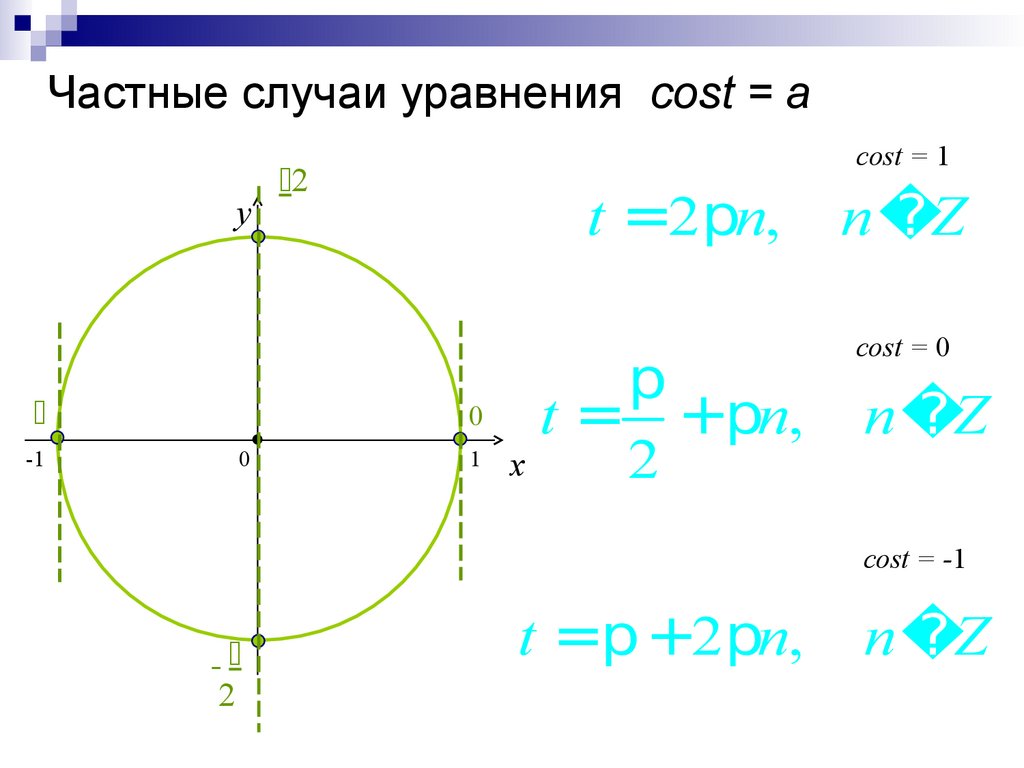
29. Частные случаи уравнения cost = a
y-1
cost = 1
2
t =2pn,
0
0
1
p
t = +pn,
x
2
n Z
cost = 0
n Z
cost = -1
2
t =p+2pn,
n Z
30. Уравнение sint = a
y-t1
1. Проверить условие | a | ≤ 1
1
t1
a
0
x
2. Отметить точку а на оси
ординат.
3. Построить перпендикуляр в
этой точке.
4. Отметить точки пересечения
перпендикуляра с окружностью.
5. Полученные точки – решение
уравнения sint = a.
6. Записать общее решение
уравнения.
-1
t1 +2pn, n Z
t =
p- t1 +2pn, n Z
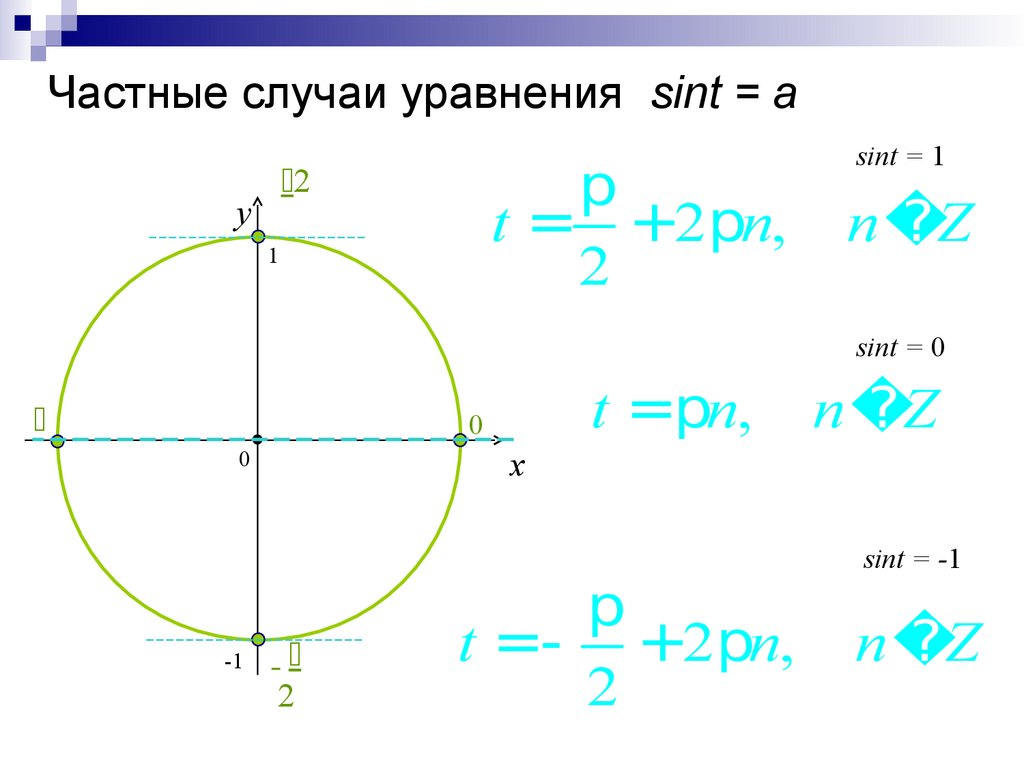
31. Частные случаи уравнения sint = a
pt = +2pn,
2
2
y
1
sint = 1
n Z
sint = 0
t =pn,
0
x
0
-1
n Z
2
p
t =- +2pn,
2
sint = -1
n Z
32. Система неравенств
33. Система неравенств:
cost a,ta
y
sint >b
1
tb
π-tb
b
-1
a
-ta
0
1
-1
x
1. Отметить на окружности
решение первого неравенства.
2. Отметить решение второго
неравенства.
3. Выделить общее решение
(пересечение дуг).
4. Записать общее решение
системы неравенств.
t ( tb +2pn; ta +2pn ] ,
n Z
34.
Учитель повышает и стимулируетинтерес учащихся благодаря
мультимедийным технологиям.
Активизируется мыслительную
деятельность и эффективность
усвоения материала благодаря
интерактивности. Это позволяет
успешно подготовить учащихся к сдаче
ЕГЭ по математике.





























 mathematics
mathematics informatics
informatics








