Similar presentations:
Решение квадратных уравнений с применением теоремы Виета
1. Решение квадратных уравнений
РЕШЕНИЕКВАДРАТНЫХ
УРАВНЕНИЙ
С применением теоремы Виета
Г.Серпухов, школа№7
2.
1) x2+6x+8=0x=-2; x=-4
5) x2-3x+2=0
2) x2-10x+9=0
6) x2+x-2=0
x=2; x=1
x=9; x=1
x=-2; x=1
3) x2-8x+7=0
7) x2+14+48=0
x=-6; x=-8
x=7; x=1
4) x2-x-2=0
x=2; x=-1
Франсуа
Виет
8) x2-2x+1=0
x=1
9) Разложите на множители:a) x2+x-2= (x+2)(x-1)
б) x2+14+48=(x+6)(x+8)
3.
САМОСТОЯТЕЛЬНАЯ РАБОТА2
1в.
1. x
2
2. x
2 x 8 0
3 x 2 0
2
3. x 6 x 7 0
2
4. x 2 x 3 0
5.
x x 2 0
2. x
2
4 x 3 0
2
3. x 2 x 24 0
2
4. x 3 x 2 0
Разложите многочлены на множители
2
x 32 x 31
3
2
б) x 3 x 2 x
а)
1.
2
2в.
6*.
а)
б)
x 2 14 x 48
3
x 8x 7 x
Решите уравнение
2
2
x 5 x 3 3;
4.
1в.2в.
7. Сократите дробь:
x 2 10 x 9
;
2 x 18
8. Найти второй корень
уравнения и значение а,
если один корень равен 2
2
x ax 12 0
2
x 6x 8
.
2
x 4x
8. Найти второй корень
уравнения и значение q,
если один корень равен -3
2
x 7 x q 0
9*. Не решая уравнения 2x2+2x-3=0, найдите:
a ) x1 x2 ;
1 1
б) .
x1 x2
a ) x1 x2 ;
2
2
2
1
б)x x .
5.
Ответы1в.
2,4;
2. -2,-1;
3. 7,1;
4. -3,1;
5. a) (x-31)(x-1)
б) x(x-2)(x-1)
1.
6.
7.
x2 6, a 4;
9*. a)
-1
б)
2,-1;
2. 3,1;
3. -6,4;
4. 2,1;
5.a) (x-6)(x-8)
б) x(x-7)(x-1)
1.
6.
-6,-5,0,1.
x 9 x 1 x 1
2 x 9
2
8.
2в.
2
3
-6,-5,0,1.
x 2 x 4 x 2
7.
.
x x 4
x
8.
x2 10, q 30.
9*. a)
-1,5
б)
1,5
6.
Решение квадратных и дробных рациональныхуравнений.
1в.
2
1) X =4;
2)
X2-9=0;
14)
0,5X =0; 4) X -5=0;
5) X2+4=0; 6)(x-2)(x+3)=0;
2
7) X +3x=0;
2
8) x -5x+6=0;
2
2
9) (X +4)(X -5)=0;
10) X3-5x2+6x=0;
11) (X2-5)(x2-4x+3)=0;
2 2
2
12) X (x -5x+6)=9(x -5x+6);
2
3)
x 2
2
x 3
0;
x 2 x 3
13)
x 3 x 2 0;
17)
x 2 3x
0;
2
x 9
15)
x 2 5x 6
0;
2
x 4x 3
16)
x
2
5 x2 4x 3
0
x 5 x 1
7.
1в.Ответы
1) 2;-2;
13) нет корней
2) 3; -3;
14) -3;
3) √5; -√5;
15) 0;
4) 0;
16) 2;
5) нет корней
17) √5; 3
6) 2;-3;
7) 0;-3;
8) 2; 3;
9) √5; -√5;
10) 0; 2; 3;
11) √5; -√5; 1; 3
12) -3; 2; 3;
8.
9. Задачи на применение теоремы Виета
ЗАДАЧИ НА ПРИМЕНЕНИЕТЕОРЕМЫ ВИЕТА
10.
Найти второй корень уравнения и значение a,если один кореньравен 2:
x2+ax-12=0
Решение.
x1·x2=-12
т.к. x1=2, то 2·x2=-12;
x2=-6.
x1+x2=-a,
2 – 6 =-a,
-4 = -a,
a=4
Ответ: x2=-6, a=4.
По теореме Виета
11.
ОдинОдин из
из корней
корней уравнения
уравнения 2x
2x22+10x+q=0
+10x+q=0
на
на 33 меньше
меньше другого.
другого. Найдите
Найдите корни
корни
Уравнения
Уравнения ии свободный
свободный член
член q.
q.
Решение.
x2+5x+0,5q=0
X1-1 корень
x2=x1+3 -2 корень
По теореме Виета
x1+x2=-5,
x1+x1+3=-5,
2x1=-8,
x1=-4, x2=-4+3=-1
x11 ·x22=0,5q
-4·(-1)=0,5q
4 = 0,5q
q=4 : 0,5
q=8
Ответ: x11=-4,x22=-1,q=8.
12.
Обучающаясамостоятельная работа
Решив каждое задание, выберите букву,
соответствующую вашему ответу.
13.
1. Решить уравнение2
2
( x 1)
( x 1) 2 x 1
;
12
3
4
Ответ : а 0 ; 2 ;
б 3 ; 4 ; в 0 ;1 1 ;
3
4. Разложите квадратный
трёхчлен 5 x 2 7 x 24
на множители
Ответ : с ( x 1,6)( x 3);
т (5 x 8)( x 3);
у (5 x 8)( x 3).
2. При каких значениях b уравнение
bx 2 x b 0 имеет один корень ?
1 1
1
1 1
Ответ : и 0; ; ; к 0; ; л 0; ; .
2 2
4
4 4
3. Решите уравнение
x 2 5 x 3 3
Ответ : г 1;0;5;6;
д 5; 1;0;6; е 6; 5;0;1.
14.
Решение №1Решение № 2.
x 2 2 x 1 x 2 2 x 1 2 x 1
0;
12
3
4
x 2 2 x 1 4 x 2 8 x 4 6 x 3 0;
bx 2 x b 0
1) если b 0, то x 0;
x 0;
2)если b 0, то D 1 4b 2
2
3 x 4 x 0;
x(3 x 4) 0;
1
x 0 или x 1 .
3
1
Ответ : 0;1 .
( В)
3
Решение №3
D 0, 1 4b 2 0;
4b 2 1;
1
b2
4
1
1
b или b
2
2
1 1
Ответ : при b ;0;
(и )
2 2.
x 2 5 x 3 3;
x 2 5 x 3 3 или x 2 5 x 3 3,
2
2
Решение№ 4
5 x 2 7 x 24;
x 5 x 6 0 ;
x 5 x 0;
x1 6 , x2 1;
x( x 5) 0
D 49 4 5 ( 24) 529, D 23;
x3 0, x4 5
7 23
7 23
1,6, x2
3;
10
10
5 x 2 7 x 24 5( x 1,6)( x 3)
(5 x 8)( x 3).
Ответ : (5 x 8)( x 3). ( т)
Ответ : 6, 5,0,1. (е)
x1













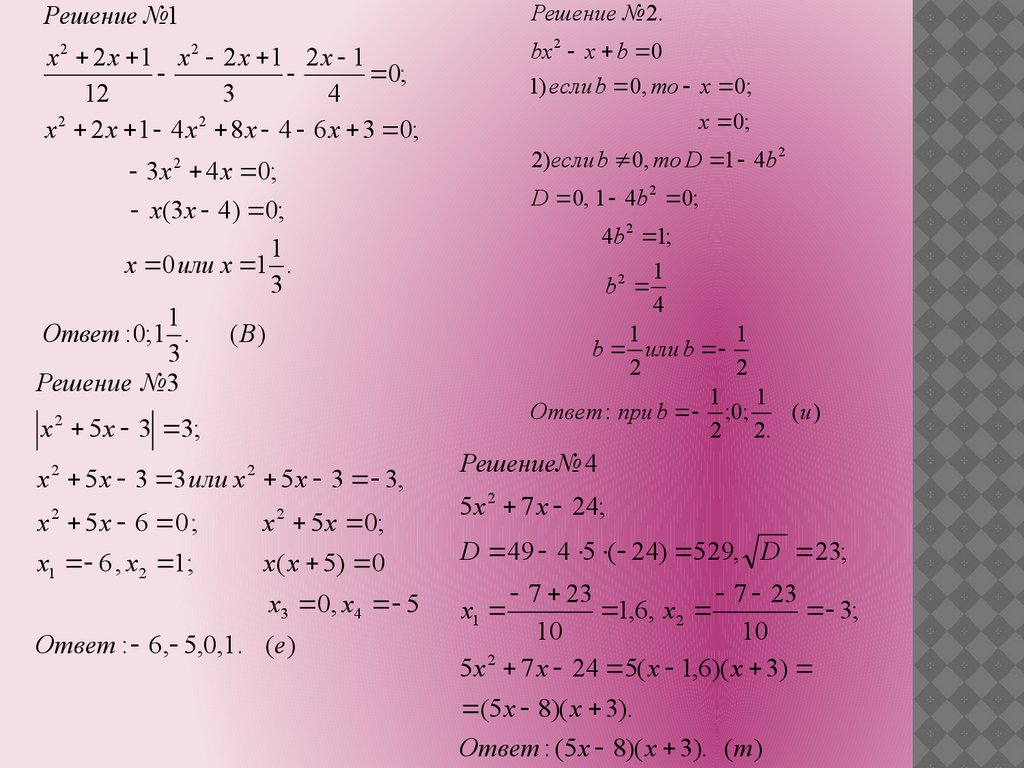
 mathematics
mathematics








