Similar presentations:
Теорема Виета. Квадратное уравнение
1. Теорема Виета
Подготовила:учитель математики МАОУ СОШ
№5 г.Лабытнанги
Вашкявичене С.Н.
2. Квадратное уравнение
Квадратным уравнением называетсяуравнение вида
ax2+bx+c=0,
где a, b, с R (a 0).
Числа a, b, с носят следующие названия:
a - первый коэффициент, b - второй
коэффициент, с - свободный член.
3.
ax bx c 02
D b 4ac
2
D<0
Корней
нет
D=0
D>0
b
x
2a
b D
x
2a
4. Приведенное уравнение
Если в уравнении вида:ax2+bx+c=0,
где a, b, с R
а = 1, то квадратное уравнение
вида x2+px+q=0 называется
приведенным.
5.
6.
Заполняем таблицу, решив квадратныеуравнения:
Приведенные
квадратные
уравнения
x2 – 2x -3=0
x2 + 5x -6 = 0
х2 - x - 12 = 0
х2 + 7x + 12 = 0
х2 - 8x + 15 = 0
X1
X2
X1 + X2
X1 ∙ X2
7.
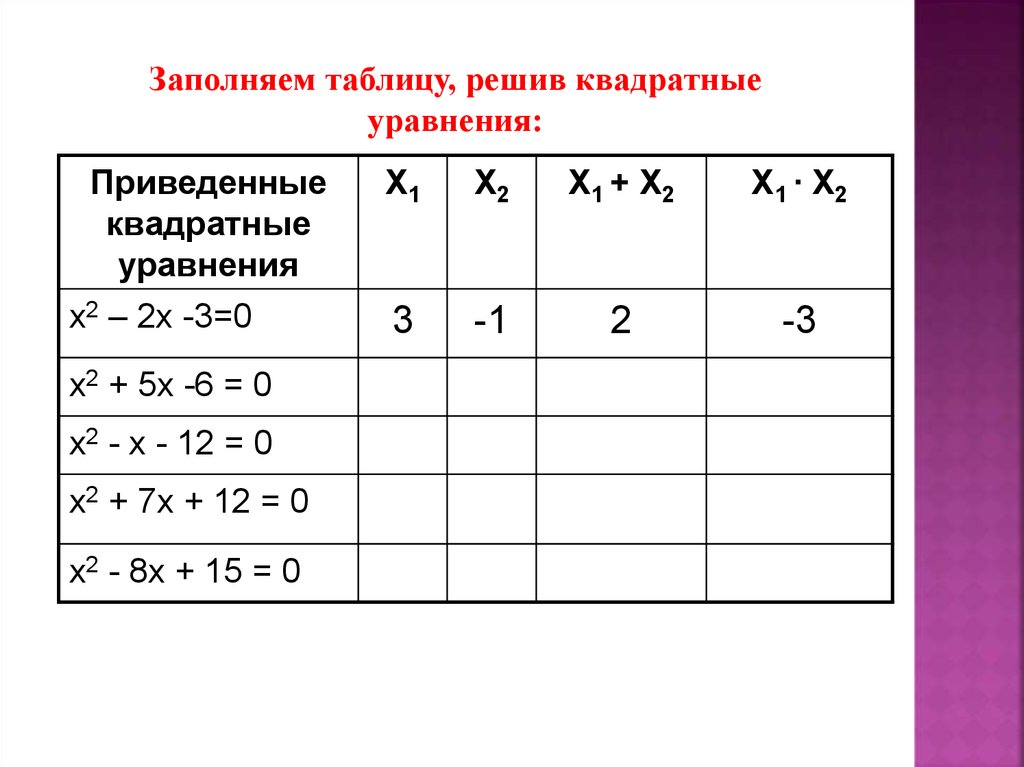
Заполняем таблицу, решив квадратныеуравнения:
Приведенные
квадратные
уравнения
x2 – 2x -3=0
x2 + 5x -6 = 0
х2 - x - 12 = 0
х2 + 7x + 12 = 0
х2 - 8x + 15 = 0
X1
X2
X1 + X2
X1 ∙ X2
3
-1
2
-3
8.
Заполняем таблицу, решив квадратныеуравнения:
Приведенные
квадратные
уравнения
X1
X2
X1 + X2
X1 ∙ X2
x2 – 2x -3=0
3
-1
2
-3
x2 + 5x -6 = 0
-6
1
-5
-6
х2 - x - 12 = 0
х2 + 7x + 12 = 0
х2 - 8x + 15 = 0
9.
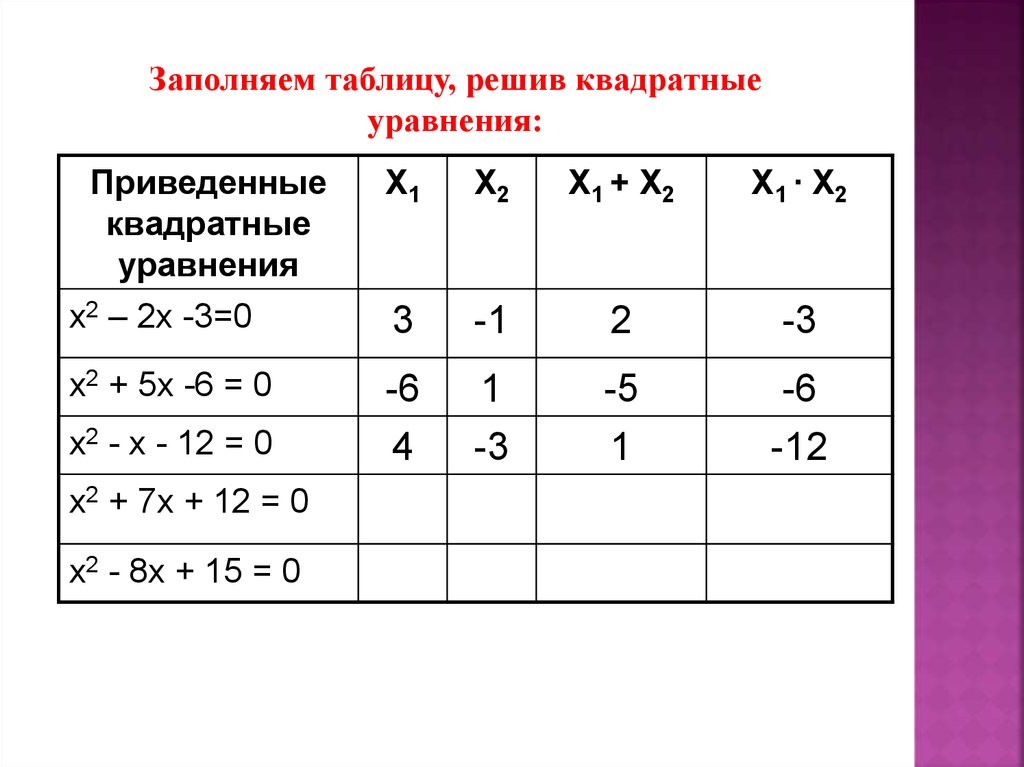
Заполняем таблицу, решив квадратныеуравнения:
Приведенные
квадратные
уравнения
X1
X2
X1 + X2
X1 ∙ X2
x2 – 2x -3=0
3
-1
2
-3
x2 + 5x -6 = 0
-6
4
1
-3
-5
1
-6
-12
х2 - x - 12 = 0
х2 + 7x + 12 = 0
х2 - 8x + 15 = 0
10.
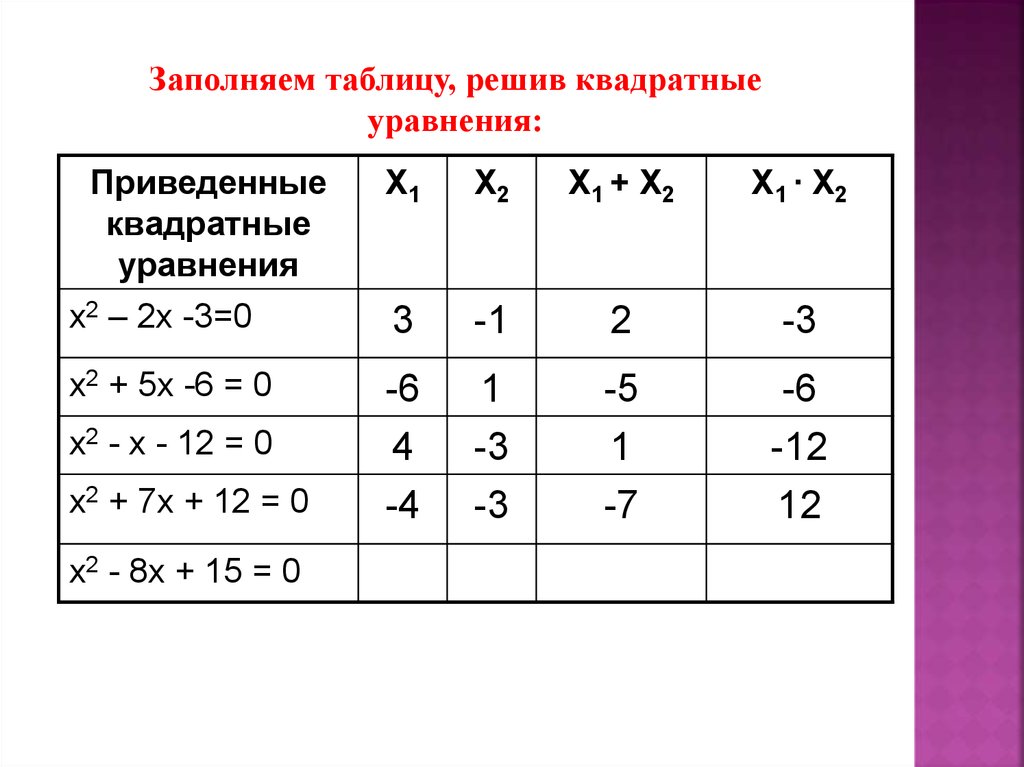
Заполняем таблицу, решив квадратныеуравнения:
Приведенные
квадратные
уравнения
X1
X2
X1 + X2
X1 ∙ X2
x2 – 2x -3=0
3
-1
2
-3
x2 + 5x -6 = 0
-6
4
-4
1
-3
-3
-5
1
-7
-6
-12
12
х2 - x - 12 = 0
х2 + 7x + 12 = 0
х2 - 8x + 15 = 0
11.
Заполняем таблицу, решив квадратныеуравнения:
Приведенные
квадратные
уравнения
X1
X2
X1 + X2
X1 ∙ X2
x2 – 2x -3=0
3
-1
2
-3
x2 + 5x -6 = 0
х2 + 7x + 12 = 0
-6
4
-4
1
-3
-3
-5
1
-7
-6
-12
12
х2 - 8x + 15 = 0
3
5
8
15
х2 - x - 12 = 0
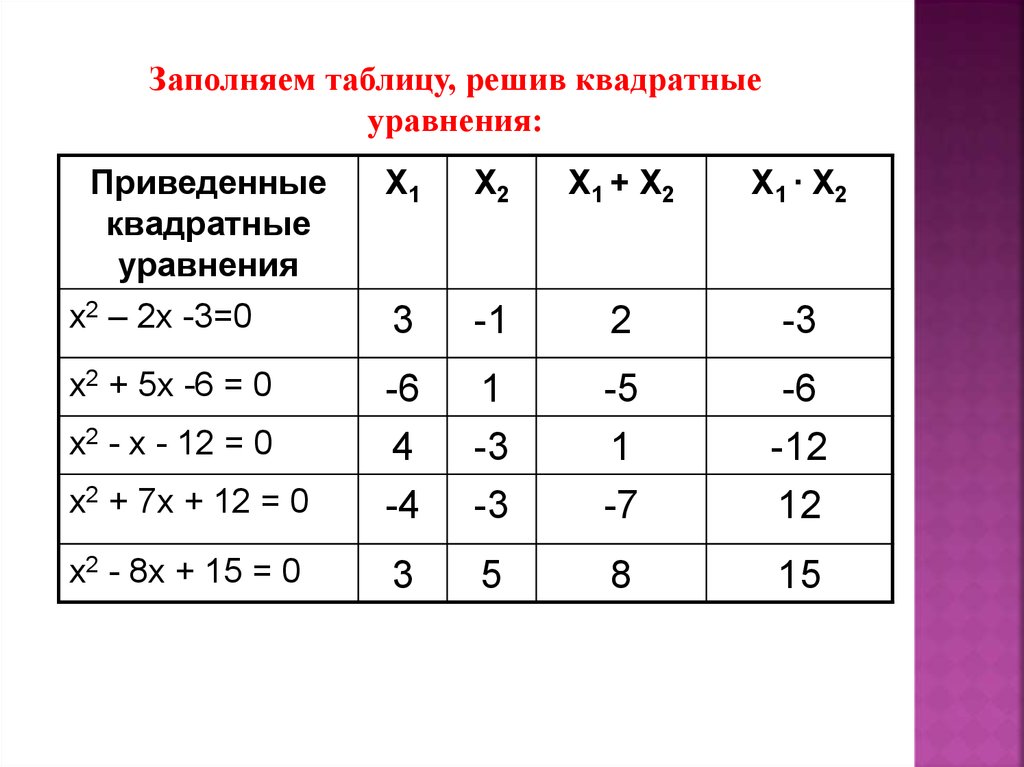
12.
Сформулируйте закономерность между корнями икоэффициентами приведенных квадратных
уравнений:
Приведенные
квадратные
уравнения
X1
X2
X1 + X2
X1 ∙ X2
x2 – 2x -3=0
3
-1
2
-3
x2 + 5x -6 = 0
-6
1
-5
-6
х2 - x - 12 = 0
4
-3
1
-12
х2 + 7x + 12 = 0
-4
-3
-7
12
х2 - 8x + 15 = 0
3
5
8
15
13. Теорема Виета
Сумма корней приведенного квадратного2
трехчлена x + px + q = 0 равна его
второму коэффициенту p с
противоположным знаком, а
произведение –
свободному члену q.
x1 + x2 = – p и x1 x2 = q
14. Теорема, обратная теореме виета
Если х1 и х2 – корни приведенногоквадратного уравнения
х2 + px + q = 0, то
x1 + x2 = - p,
x1 ∙ x2 = q.
15. Вычисление корней
Так, еще не зная, как вычислитькорни уравнения:
2
x + 2x – 8 = 0,
мы, тем не менее, можем сказать,
что их сумма должна быть равна
– 2, а произведение должно
равняться –8.
16. Пример:
Теорема Виета позволяет угадыватьцелые корни квадратного трехчлена.
Так, находя корни квадратного уравнения
2
x – 7x + 10 = 0,
можно начать с того, чтобы попытаться
разложить свободный член (число 10)
на два множителя так, чтобы их сумма
равнялась бы числу 7.
17. Решение:
Это разложение очевидно:10 = 5 × 2,
5 + 2 = 7.
Отсюда должно следовать, что
числа 2 и 5 являются искомыми корнями.
18. Подведение итогов урока:
Сконструировать квадратное уравнение,зная его корни:
Х1
Х2
2
-3
1
5
-6
-4
-2
3
Уравнение
19. Подведение итогов урока:
Ответ:Х1
Х2
Уравнение
2
-3
x2 – 2x -3=0
1
5
x2 –x + 5=0
-6
-4
x2 + 6x - 4=0
-2
3
x2 + 2x +3=0


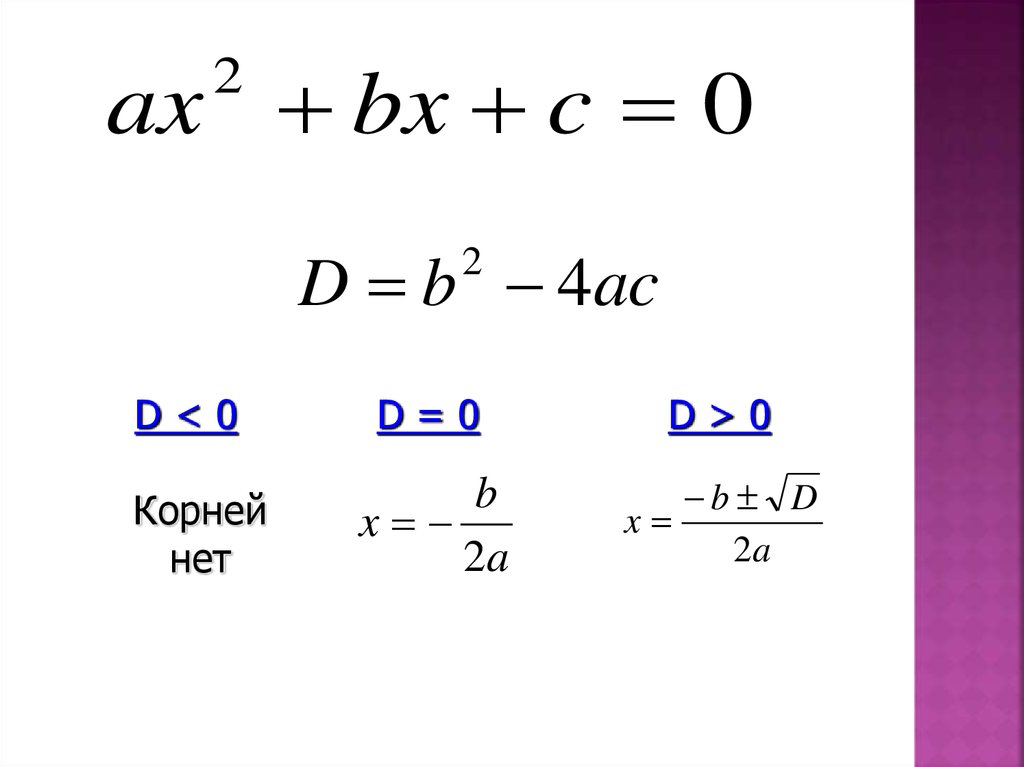













 mathematics
mathematics








