Similar presentations:
Приведенные квадратные уравнения. Теорема Виета
1.
1) 2 õ 4 õ 30 08)13 õ õ 7 0
2) õ 4 õ 7 0
9) y 4 y 5 0
2
.
3
3) õ 2 õ 0
2
4)5 õ 3 0
5) õ 5 õ 6 0
2
6)5 õ 6 õ 7 0
2
6 y
7)
0
y
4
2
2
10) x 15 x 7 0
3
11) x 7 0
12) x 3 0
2
13) x 15 x 36 0
2
2.
.5) õ 5õ 6 0
2
1) 2 õ 4 õ 30 0
2
6)5 õ 6 õ 7 0
2
9) y 4 y 5 0
2
13) x 15 x 36 0
3) õ 2 õ 0
2
12) x 2 3 0
2
3.
Приведенные квадратныеуравнения.
Теорема Виета.
4. Приведенные квадратные уравнения
ax² +bx +c =0, a≠0а=1
x² +bx +c =0
x²+px+q=0
5. Исследовательская работа
6.
.5) õ 5õ 6 0
2
1) 2 õ 4 õ 30 0
2
6)5õ 6 õ 7 0
2
9) y 4 y 5 0
2
13) x 15 x 36 0
2
7.
Теорема Виета.Если числа х1 и х2
являются корнями уравнения
х2+рх+q=0
то справедливы формулы
x1 x2 p
x1 x2 q
т.е.сумма корней приведённого квадратного
уравнения равна второму коэффициенту, взятому
с противоположным знаком, а произведение
корней равно свободному члену.
8. Историческая справка
9.
Франсуа Виет(1540-1603)Родился в 1540 году в городе Фонтенле-Конт,
в
провинции
Пуату.
По
образованию был юристом, но глубоко
занимался многими науками, прежде всего
астрономией,
астрологией
и
даже
криптографией (тайнописью). Всё это
заставило
Виета
обратиться
к
тригонометрии и алгебре, в которых он
сделал немало открытий.
Ему
принадлежит
установление
единого способа решения уравнений 2-й, 3й, и 4-й степеней, но больше всего сам
ученый оценил установление зависимости
между корнями и коэффициентами
уравнений. Именно за это его до сих пор
называют «отцом алгебры».
Сам «отец алгебры» не признавал
слово «алгебра», считал его языческим,
варварским. То, чем он занимался, Франсуа
Виет
называл
«аналитическим
искусством».
В 2011 году исполнилось 420 лет со
дня опубликования теоремы Виета,
ставшей
ныне
самым
знаковым
утверждением школьной алгебры.
10. Теорема Виета для приведенного квадратного уравнения:
Сумма корней приведённого квадратногоуравнения равна второму коэффициенту,
взятому с противоположным знаком, а
произведение корней равно свободному
члену.
õ px q 0
2
x1 + x2 = -p
x1 · x2 = q
11. Применение теоремы Виета
а)для нахождения суммы и произведения корнейприведенного квадратного уравнения:
1. х²-16х+28=0
2. х²-12х-45=0
3. х²-27х=0
4. х²-12=0
х1 + х2= 16
х1·х2=28
х1 + х2=12
х1·х2=-45
х1 + х2=27
х1·х2=0
х1 + х2= 0
х1·х2=-12
12. Применение теоремы Виета
Б) Для проверки правильности решения(Являются ли данные числа корнями уравнения?)
õ 7õ 6 0
2
õ õ 20 0
2
õ 3õ 18 0
2
2и3
нет
2 и -10
нет
1и6
да
-5 и 4
нет
-4 и 5
да
-2 и 9
-3 и 6
-6 и 3
нет
нет
да
13. в) для составления квадратного уравнения по заданным корням.
Применение теоремы Виетав) для составления квадратного уравнения по
заданным корням.
Задача: Составить квадратное уравнение, корнями
которого являются числа 8 и – 5.
-р = 8 + (- 5) и q = 8 (- 5)
р=-3
q = - 40
x px q 0
2
x 3x 40 0
2
14. Применение теоремы Виета
г) Не применяя формулу корней , найти второй кореньх²-7х+10=0
õ1 2
15. Применение теоремы Виета д)для решения уравнений
õ2 2009 õ 2010 0õ1 õ2 2009
õ1 õ2 2010,
õ1 1
õ2 2010
16. Продолжите фразу:
“Сегодня на уроке я познакомился...”17. Применение теоремы Виета ж)для нахождения коэффициентов уравнения
1.В уравнении х2 - 12х + с = 0, один из корней х1=5. Найдитедругой корень и коэффициент с.
5 õ2 12, õ2 7
ñ 5 7 35
2. В уравнении х2 +рх + 15 = 0, один из корней х1=3. Найдите
другой корень и коэффициент р.
3 õ2 15, õ2 5
3 5 p, p 8
18. Заполните таблицу.
1.Найдите сумму и произведениекорней уравнения х2 + 8х +7 = 0.
2.Решите уравнение х2 + 9х + 20 = 0.
õ1 õ2 8
õ1 õ2 7
õ1 4
õ2 5
3.Определите знаки корней уравнения
х2+5х-36=0.
4.Составьте квадратное уравнение,
корнями которого являются числа
2 и 5.
5.Разложите квадратный трехчлен на
множители х2+2х-48.
6.В уравнении х2+pх-42=0 один из
корней равен 7. Найдите другой корень
и коэффициент p.
êîðíè ðàçíûõ çíàêîâ
õ2 7 õ 10 0
õ2 2 õ 48 õ 6 õ 8
õ2 6
p 1
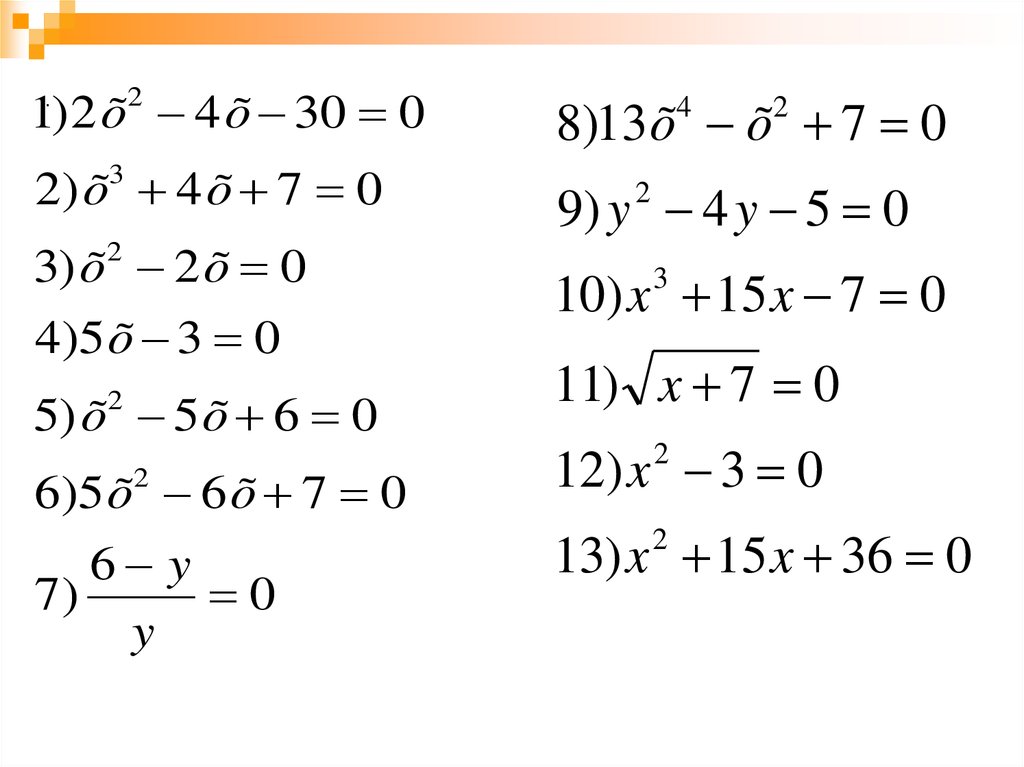
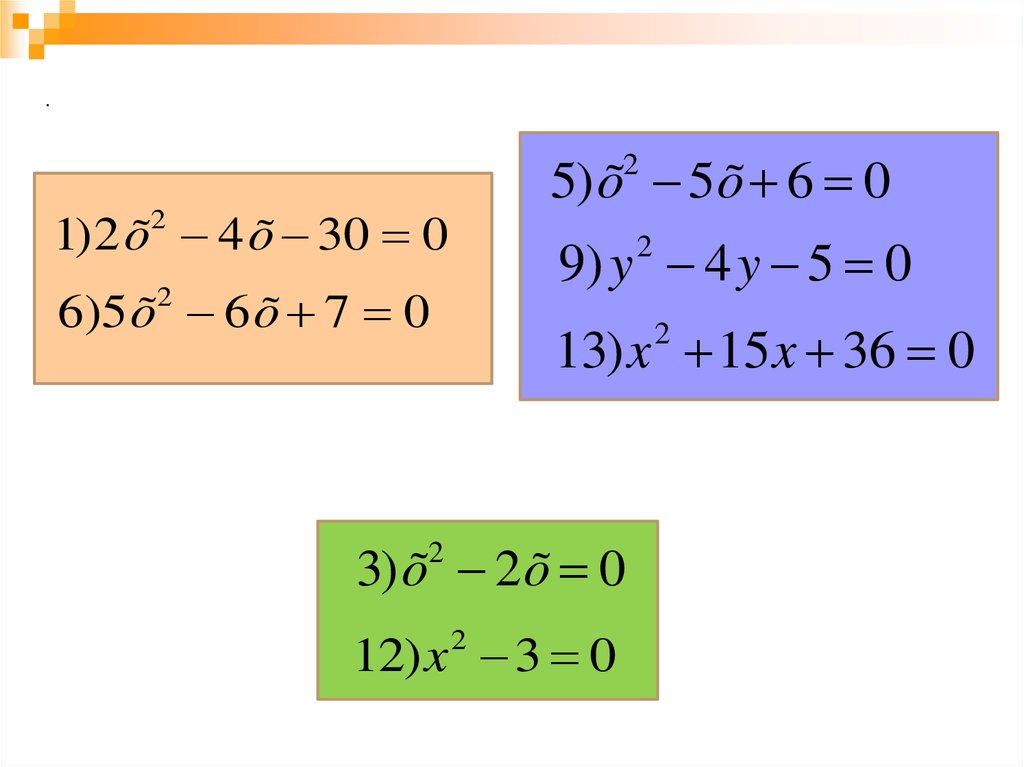

















 mathematics
mathematics








