Similar presentations:
Целое уравнение и его корни
1. ЦЕЛОЕ УРАВНЕНИЕ И ЕГО КОРНИ
9 классГБОУ СОШ № 544
учитель математики:
Зотова Ирина Вячеславовна
2. Психологическая установка
• продолжаем обобщать и углублять сведенияоб уравнениях;
• знакомимся с понятием целого рационального
и дробного рационального уравнения;
• с понятием степени уравнения;
• формируем навыки решения уравнений.;
• контролируем уровень усвоения материала;
• На уроке можем ошибаться, сомневаться,
консультироваться.
• Каждый учащийся сам себе дает установку.
3. План урока
Какие уравнения называются целыми?
Что называется степенью уравнения?
Сколько корней имеет уравнение n-й степени?
Методы решения уравнений первой, второй и
третьей степени.
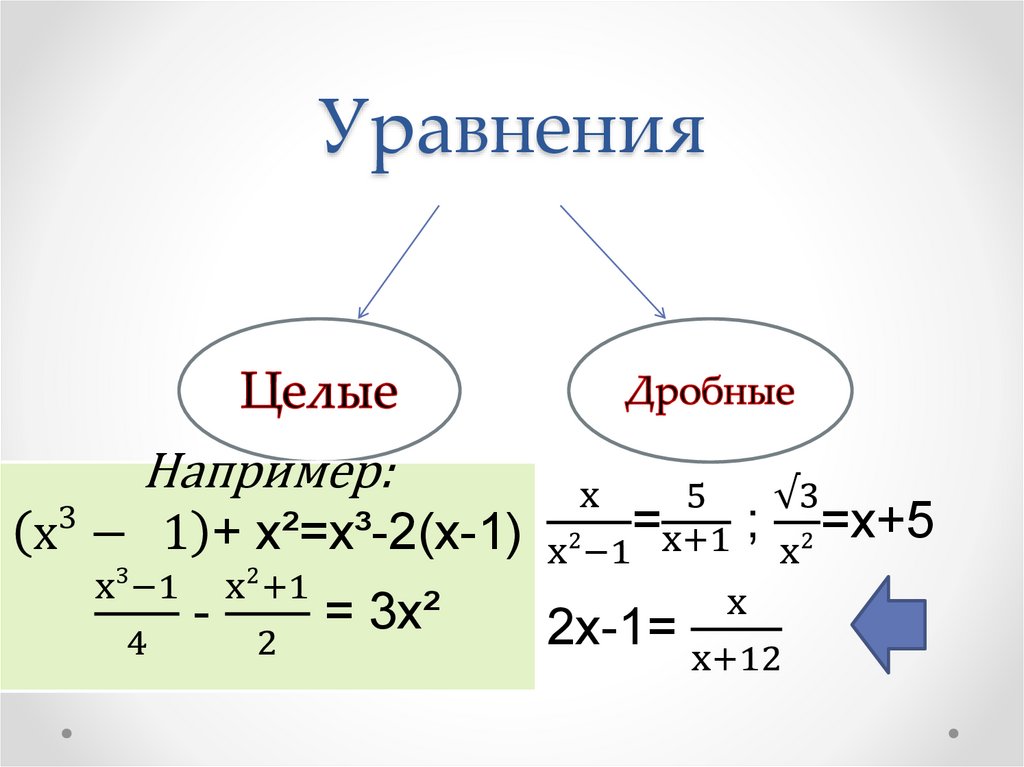
4. Уравнения
Например:x³ − 1 + x²=x³-2(x-1)
x³−1
4
-
x²+1
2
= 3x²
x
5
√3
=x+1 ; =x+5
x²−1
x²
x
2x-1=
x+12
5.
ЦЕЛЫМ УРАВНЕНИЕМ СОДНОЙ ПЕРЕМЕННОЙ
НАЗЫВАЕТСЯ
УРАВНЕНИЕ, ЛЕВАЯ И
ПРАВАЯ ЧАСТИ
КОТОРОГО- ЦЕЛЫЕ
ВЫРАЖЕНИЯ
6.
Если уравнение с одной переменнойзаписано в виде
P(x) = 0, где P(x)- многочлен стандартного вида,
то степень этого многочлена называют
степенью данного уравнения
x 5 -2x³+2x-1=0 (5-я степень)
x 4 -14x²-3=0 (4-я степень)
7.
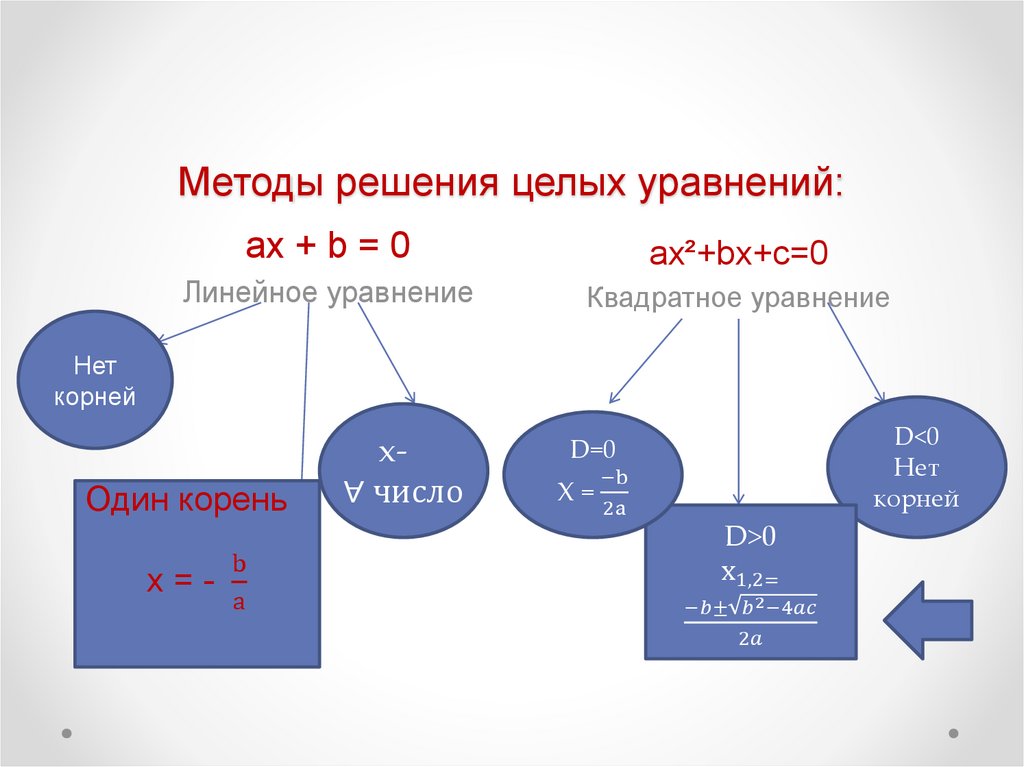
8. Методы решения целых уравнений:
ax + b = 0ax²+bx+c=0
Линейное уравнение
Квадратное уравнение
Нет
корней
Один корень
x=-
b
a
x∀ число
D<0
Нет
корней
D=0
X=
−b
2a
D>0
x1,2=
−










 mathematics
mathematics