Similar presentations:
Целые уравнения
1.
ГОУ РК «РЦО» структурноеподразделение ЦДОДИ в
Республике Коми
Автор: Хребтова Ольга Евгеньевна
Год создания: 2014
Место создания: ЦДОДИ
30.11.15
2. Девиз нашего урока: «Чем больше я знаю, тем больше умею.»
Эпигаф:Кто ничего не замечает,
Тот ничего не изучает.
Кто ничего не изучает,
Тот вечно хнычет и скучает.
(поэт Р.Сеф).
3. Математический диктант
1.Вставить недостающиеслова и указать соответствия
1.Что называется
уравнением?
1. Найти все его … или
доказать, что … нет.
2.Что называется
корнем уравнения?
2. ……, содержащее
переменную.
3.Что значит решить
уравнение?
3. ……., при котором
уравнение обращается
в верное числовое
равенство.
4. Решить уравнения устно:
а) x² = 0б) 3x – 6 = 0
в) x² – 9 = 0
г) x(x – 1)(x + 2) = 0
д) x² = – 25
5. Решить уравнение:
х⁴-6х²+5=06. Целое уравнение и его корни
7. Цели урока:
обобщить и углубить сведения обуравнениях
знакомство с понятием целое
уравнение
знакомство с понятием степень
уравнения
формирование навыков решения
уравнений
8. Уравнения
x5
2
x 1 x 1
3
x
2
x 5
x3 1 x 2 1
3x 2
4
2
( x 3 1) x 2 x 3 2( x 1)
x
2x 1
x 12
целые
уравнения
дробные
уравнения
9. Целое уравнение
Целым уравнением с однойпеременной называется уравнение,
левая и правая части которого
целые выражения.
10. Степень уравнения
Если уравнение с однойпеременной записано в виде P(x)=0,
где P(x) – многочлен стандартного
вида, то степень этого многочлена
называют степенью уравнения, т.е
наибольшая из степеней
одночленов.
Примеры: x⁵-2x³+2x-1=05-я
степень
4-я
x⁴-14x²-3=0
степень
11. Какова степень уравнения?
5а) 2х²-6х⁵+1=0
2
г) (х+8)(х-7)=0
6
б) х⁶-4х²-3=0
1 5
х 0
7
в)
5х(х²+4)=17
д)
х х
5
2 4
5
1
3
е) 5х-
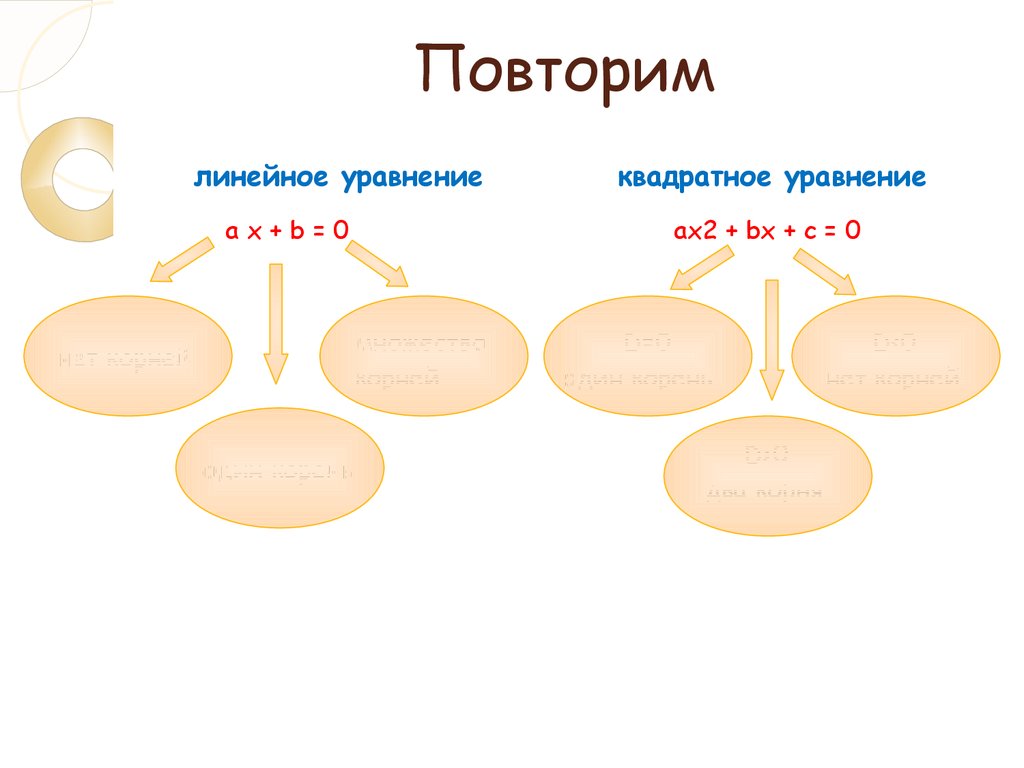
12. Повторим
линейное уравнениеaх+b=0
aх2 + bx + c = 0
множество
корней
нет корней
один корень
квадратное уравнение
D=0
один корень
D>0
два корня
D<0
нет корней
13. Уравнение первой степени
14. Уравнение третьей степени
Решить уравнениеx3 8x 2 x 8 0
Решение: разложим левую часть
уравнения 2на множители
x ( x 8) ( x 8) 0
( x 8)( x 2 1) 0
x 8 0
x2 1 0
x1 8, x2ответ
1, x3 1
15. Решить уравнение:
(8x-1)(2x-3)-(4x-1)²=38Решение:Раскроем скобки и приведем
подобные слагаемые
16x²-24x-2x+3-16x²+8x-1-38=0
-18x-36=0
ПРОВЕРЬТЕ СЕБЯ!
x+2=0
x=-2
Ответ: x=-2
16. Решим биквадратное уравнение:
Х⁴ - 5 х² - 36 = 0Сделаем замену: х² = а, а≥ 0
а² - 5а -36 =0
D = 169
а1= -4 (не подходит, т.к. а≥0)
а2 = 9
Х² = 9
х1 = 3 и х2 = -3
Ответ: 3 и -3.
17. Решить уравнение:
х⁴-6х²+5=0Ответ: 1, -1, Ѵ5, - Ѵ5
18. Установите соответствие: Уравнение способ.
Образец текстаВторой уровень
Третий уровень
Четвертый уровень
Пятый уровень
19. Тест
1) Определите степень уравнения( x 2 3) 5 x( x 1) 15
а) 2
б) 3
в) 1
2) Какие из чисел являются корнями
x( x 1)( x 2 ) 0?
уравнения
а) -1
б) 0
в) 2
3) Решите уравнение 9 x 3 27 x 2 0
а) 0;-3
б) -3;0;3
в) 0;3
20.
1)Какое уравнение называется
целым и как его отличить от
дробного?
2)
Что такое степень уравнения?
3)
Что такое корни уравнения?
4)
5)
Сколько корней может иметь
уравнение 1 степени?
Сколько корней может иметь
уравнение 2 степени?
21. Домашнее задание:
Подумай и ответь на вопрос: «Сколькокорней может иметь целое уравнение с
одной переменной 2-ой, 3-ой, 4-ой, пой степени ?»
Реши биквадратные уравнения:




















 mathematics
mathematics