Неравенства второй степени с одной переменной

1. Тема урока

ТЕМА УРОКА
Решение неравенств
второй степени с одной
переменной

2. ЦЕЛЬ УРОКА

1.
2.
3.
4.
Повторить знания об уравнениях.
Определить вид неравенств
второй степени с одной
переменной и алгоритм решения.
Научиться решать квадратные
неравенства графически.
Воспитывать в себе
самостоятельность , аккуратность.

3.

УСТНАЯ РАБОТА
УРАВНЕНИЯ
ЦЕЛЫЕ
СТЕПЕНЬ
УРАВНЕНИЯ
БИКВАДРАТ
НЫЕ
ДРОБНЫЕ
РАЦИОНАЛЬН
ЫЕ
АЛГОРИТМ
РЕШЕНИЯ

4. ОПРЕДЕЛИТЕ ВИД УРАВНЕНИЙ:

(у³-9у) =0,
(у²+у-12)
1__ - _1_ = _1__ ,
(х-7) (х-1) (х-10)
Х² - 5Х+7=0,
(Х³)² - 5Х + 2=0
2Х³ + 6Х - Х² + 9 =8.

5. ПРОВЕРОЧНАЯ РАБОТА

Решите одно целое уравнение по выбору:
у³-6у=0,
«3»балла
3х³-х²+18х-6=0,
«4»балла
(х²-1)(х²+1)-4(х²-11)=0
«5»баллов

6. ОТВЕТЫ

Уравнение
у³-6у=0
1
2
3
корень корень корень
0
- √6
√6
3х³-х²+18х-6=0
1/3
(х²-1)(х²+1)-4(х²-11)=0
Нет
корней

7. Изучение новой темы

ИЗУЧЕНИЕ НОВОЙ ТЕМЫ
Неравенства вида ах²+вх+с>0 и ах²+вх+с<0 неравенства второй степени с одной переменной,
где х- переменная, а,в,с- некоторые числа и а ≠0.
Графический
способ
решения
квадратного
неравенства:
1)найти корни квадратного трехчлена ах²+вх+с и
отметить их на оси х;
2)схематически провести параболу через данные
точки на оси х; определить направление ветвей;
3)найти
на
оси
х
промежутки,
которые
удовлетворяют неравенству.

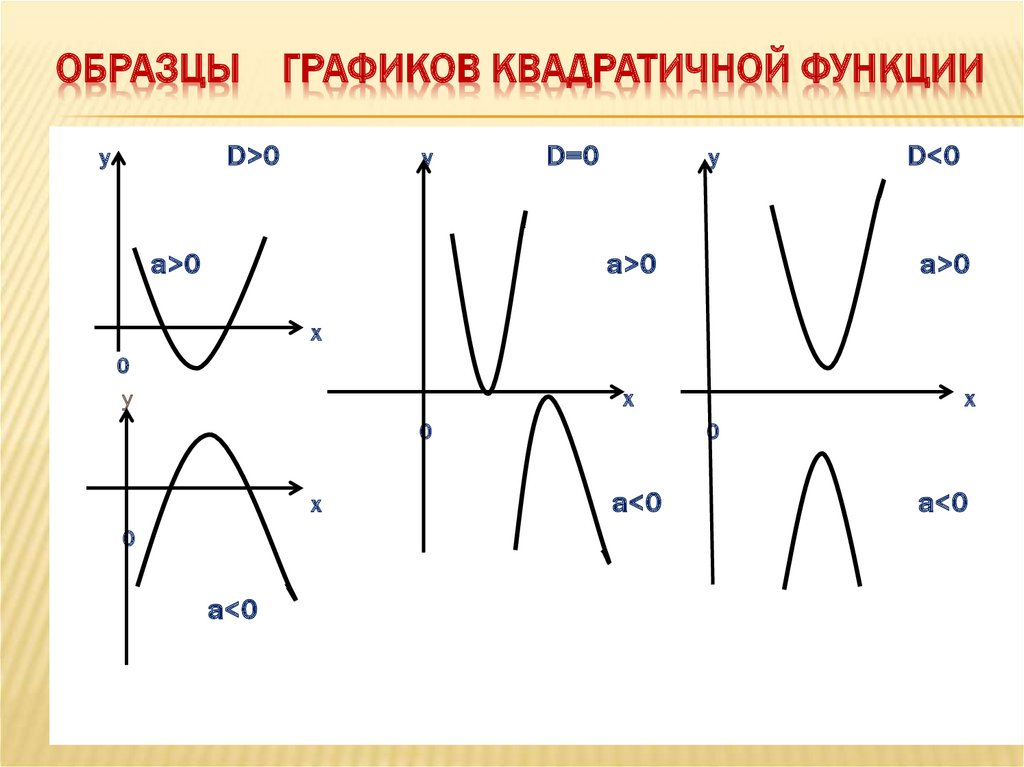
8. Образцы Графиков квадратичной функции

ОБРАЗЦЫ ГРАФИКОВ КВАДРАТИЧНОЙ ФУНКЦИИ
D>0
у
у
a>0
D=0
у
a>0
D<0
a>0
х
0
у
х
0
х
0
а<0
х
0
a<0
a<0

9. Работа по учебнику

РАБОТА ПО УЧЕБНИКУ
1. Прочитайте правила п.14
страницы 83,85.
2.Решить неравенства №304(а, в),
305(а),
308(а).

10. МИНУТА ОТДЫХА

Написать
глазами, носом в воздухе
цифры 0, 8; 5, 0; 5, 6; 4,1.
Составьте
О
из этих пар цифр числа.
каких знаменательных датах говорят
эти пары цифр?

11. самостоятельная работа

САМОСТОЯТЕЛЬНАЯ РАБОТА
Из сборника экзаменационных работ по
алгебре за 9 класс.
Работа 4. Вариант 1. Вариант 2. №5.

12. Итог урока

ИТОГ УРОКА
Чему научились на уроке?
Домашнее задание. П.14, № 304(2 столбик),
305(в), 307(б).
Творческое задание на «5» баллов
а) (2х-3)(5х+2)≥(2х-3)(3х-8),
б) (3х-7)²≤(7х-3)².