Решение неравенств второй степени с одной переменной

1. «Решение неравенств второй степени с одной переменной»

Учитель математики
МКОУ «Виноградненская
СОШ имени Дедова Ф.И.»
Кравченко Татьяна
Константиновна

2. Цель урока

повторить, систематизировать и
обобщить знания, умения и навыки по
теме «Решение неравенств второй
степени с одной переменной»

3. План урока

Устная работа (повторение основных
утверждений по пройденной теме)
Самостоятельная работа базового
уровня
Решение неравенств повышенного
уровня сложности: на 2 балла; на 4
балла; на 6 баллов.
Подведение итогов урока

4. Девиз урока

« Реши сам помоги другу!»

5. Тема урока:

«Решение неравенств
второй степени с
одной переменной»

6.

Какие неравенства называются
неравенствами второй степени с
одной переменной?

7.

1. Из предложенных неравенств выберите квадратные:
5 3x 0
9 x 3 18 x 2 x 2 0
2x
x 3
9
3
2
x 3x 1
x 4 x 45 0
2
2
x 2x 8 0
2

8.

На чем основано решение
неравенств второй степени с
одной переменной?

9.

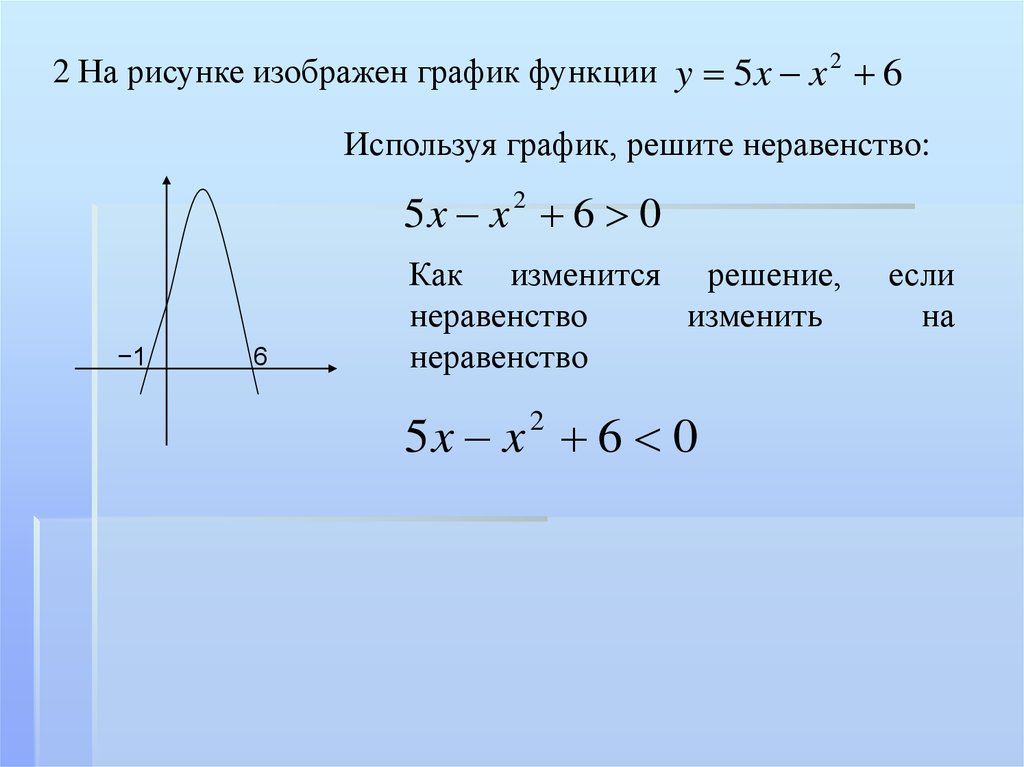
2 На рисунке изображен график функции y 5x x 2 6
Используя график, решите неравенство:
5x x 6 0
2
−1
6
Как изменится решение,
неравенство
изменить
неравенство
5x x 6 0
2
если
на

10.

3 Дана функция, назовите нули функции:
f ( x) 3x x
2
f ( x) x 4
2
f ( x) x x 6
2

11.

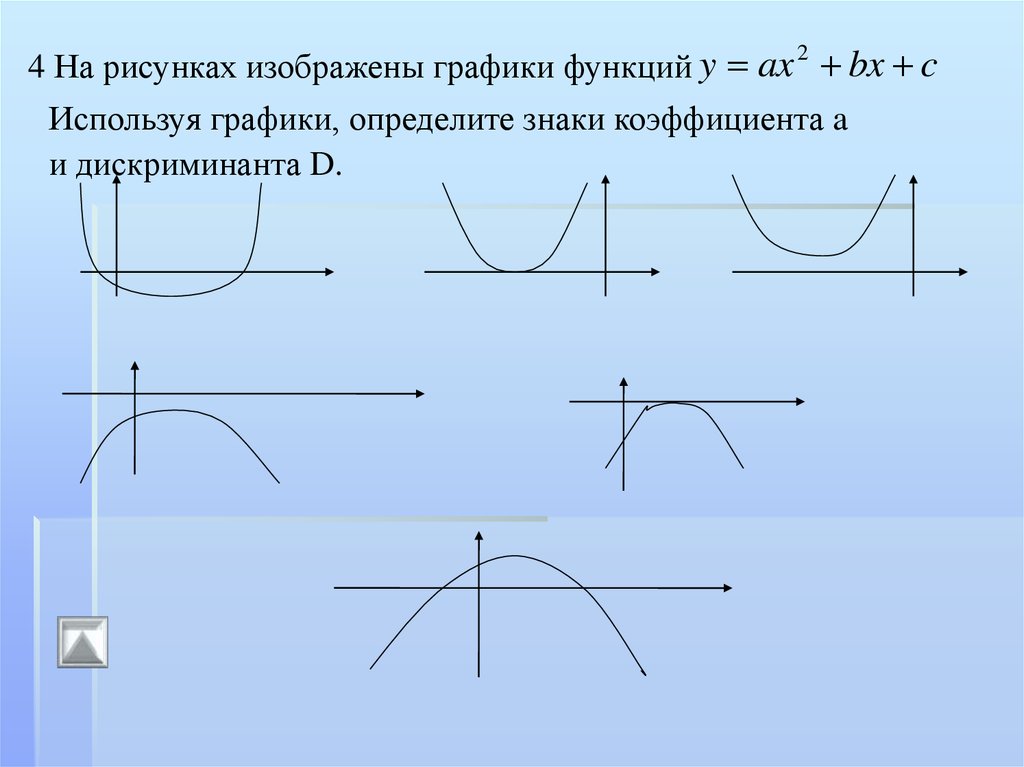
2
4 На рисунках изображены графики функций y ax bx c
Используя графики, определите знаки коэффициента a
и дискриминанта D.

12. Самостоятельная работа

Вариант 1
Вариант 2
Решите неравенства :
Решите неравенства :
1) x 2 x 6 0
1) x 4 x 5 0
2) 3 x 2 x 0
2)3 x x 2 0
3) x 2 1 0
3) x 2 9 0
4)4 x( x 1) 3
4 ) 4 x ( x 2) 5
2

13. Проверим свою работу

Вариант 1
Вариант 2
ответы :
ответы :
1) ; 3] [2; )
1) 5;1
1
2) 0;
3
3) 1;1
1
2)( ;0) ;
3
3)( ; 3] [3; )
4)( ; 0,25) (1,5; )
4)( 2,5;0,5)

14. Групповая работа

«Золотой призер
урока»
«Серебряный
призер урока»
«Бронзовый
призер урока»
х²-9>0
х²-2х<0
х²+х+7<0
х²+х-6≤0
х²+3х-4>0
-х²+3х-2≥0
2х²-9х+4<0
-4х²+8х-4≤0
3х²-4х+1≥0

15. Проверка решения

1.
2.
3.
4.
5.
6.
7.
8.
9.
(-∞;-3)U(3;+ ∞)
(0;2)
Нет решений
[-3;2]
(-∞;-4)U(1;+ ∞)
[1;2]
1
( 2 ;4)
(-∞; ∞)
1
(-∞; 3 ]U[1;+ ∞)

16. Подведём итоги

При изучении данной темы вы познакомились с
понятиями:
Определение квадратного неравенства
Определение решения неравенства
Определение равносильного неравенства
Определение равносильного преобразования
Определение системы неравенств
Определение решения системы неравенств

17. Рефлексия

что сегодня нового вы узнали на
уроке?
что научились делать на уроке?
где полученные знания вы можете
применить?

18. Что интересного будет на следующем уроке?

решение неравенств методом
интервалов
решение неравенств, содержащих
модуль.

19. Домашняя работа

№ 315
(а, б, в)

20. 1 группа №1159 №1181 2 группа №1160 №1185 3 группа № 1195 №1241