Функции и их графики

1.

Благова Наталья Александровна
МОУ Гимназия №65 им.Н.Сафронова

2.

Содержание.
Построение графиков функций y=af(x)
Построение графиков функций y=af(x)+n
Построение графиков функций y=af(x-m)
Построение графиков функций y=af(x-m)+n
Другие примеры

3.

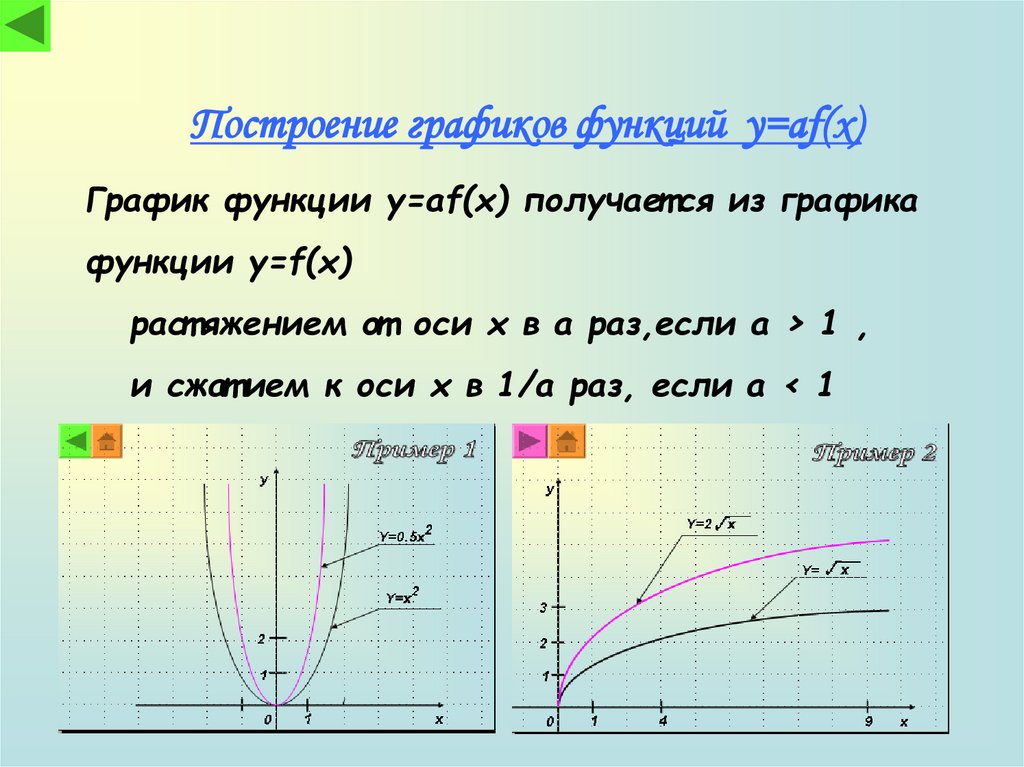
Построение графиков функций y=af(x)
График функции y=af(x) получает ся из графика
функции y=f(x)
раст яжением от оси x в a раз,если a > 1 ,
и сжат ием к оси x в 1/a раз, если a < 1

4.

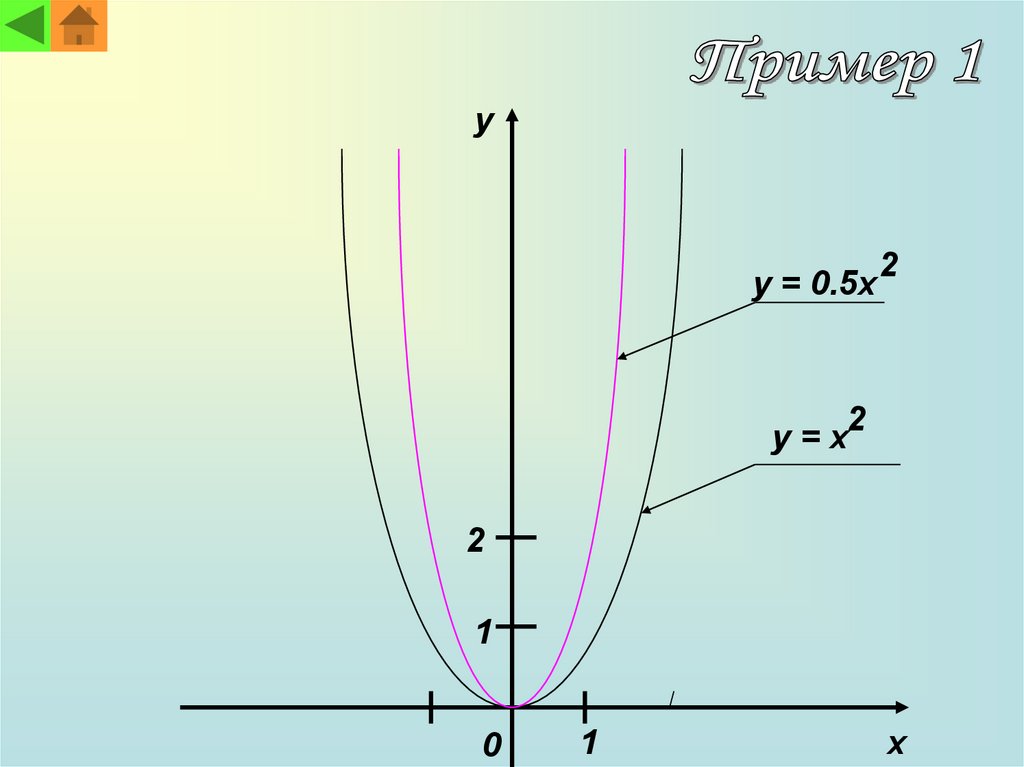
y
y = 0.5x
2
2
y=x
2
1
0
1
x

5.

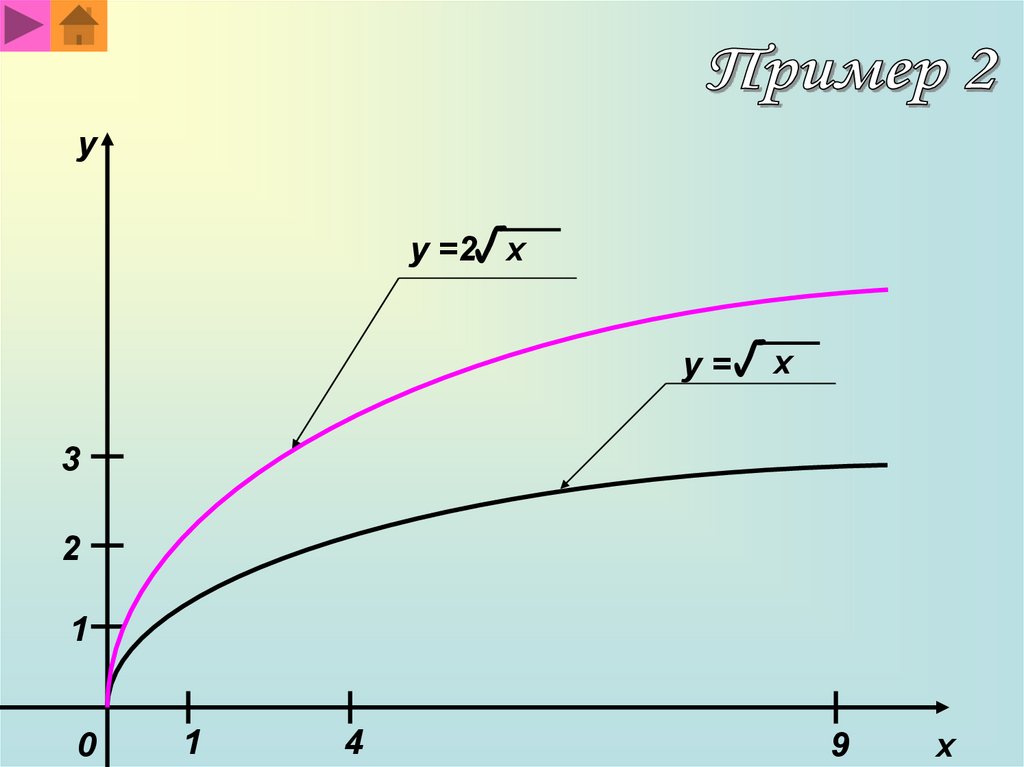
y
y =2√ x
y =√ x
3
2
1
0
1
4
9
x

6.

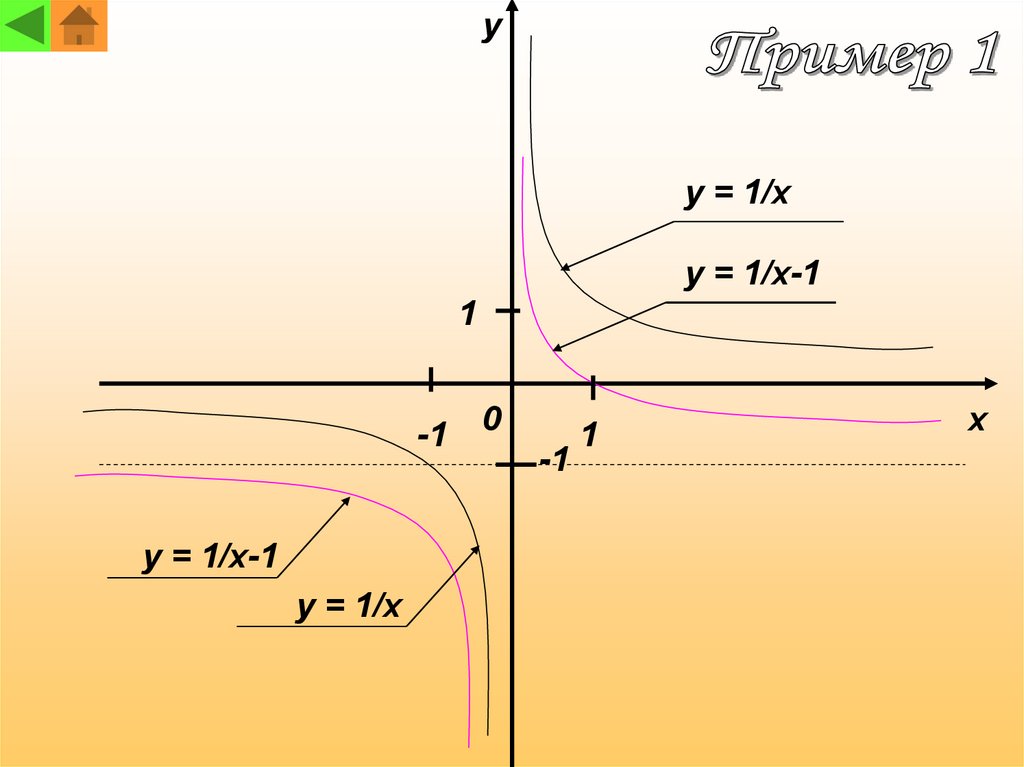
Построение графиков функций y=af(x)+n
График функции y=af(x)+n получает ся из
графика функции y=af(x) с помощью
параллельного переноса вдоль оси y
на n единиц вверх, если n > 0, или
на -n единиц вниз, если n < 0.

7.

y
y = 1/x
y = 1/x-1
1
-1 0
y = 1/x-1
y = 1/x
-1
1
x

8.

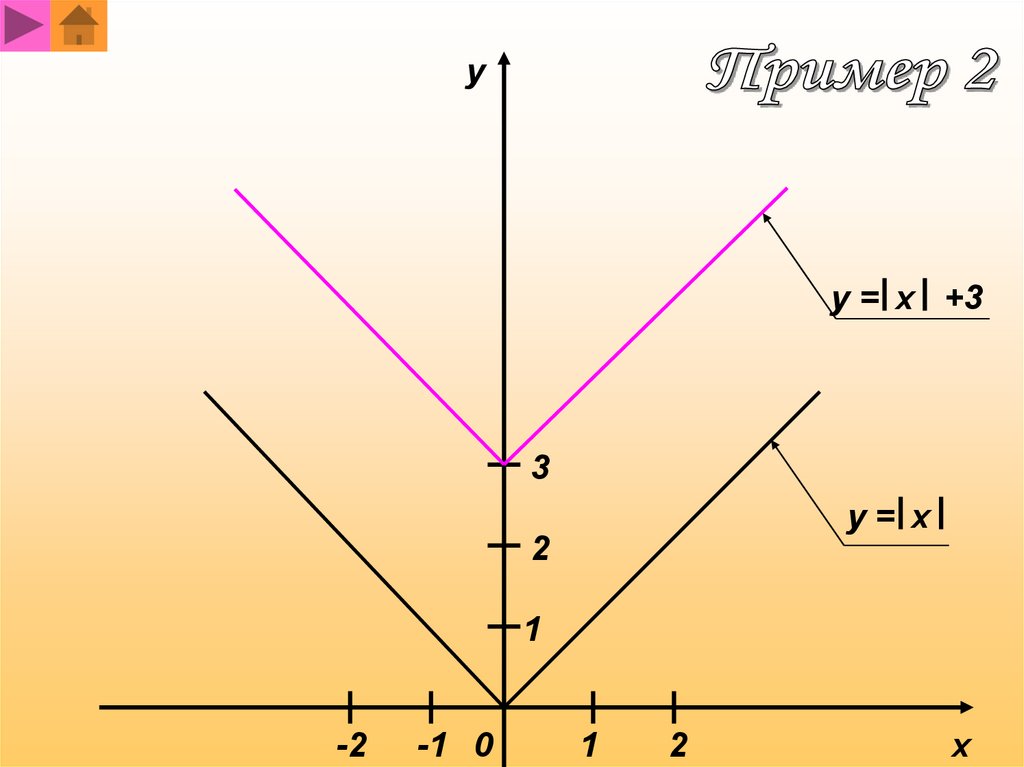
y
y = x +3
3
y= x
2
1
-2
-1 0
1
2
x

9.

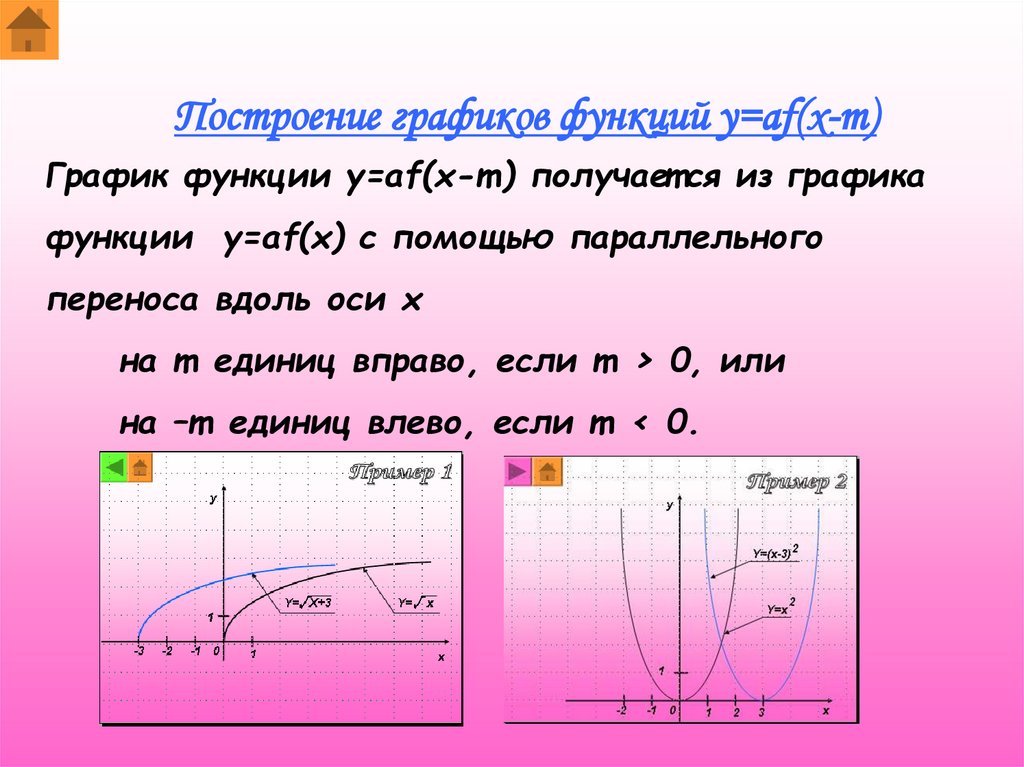
Построение графиков функций y=af(x-m)
График функции y=af(x-m) получает ся из графика
функции y=af(x) с помощью параллельного
переноса вдоль оси x
на m единиц вправо, если m > 0, или
на –m единиц влево, если m < 0.

10.

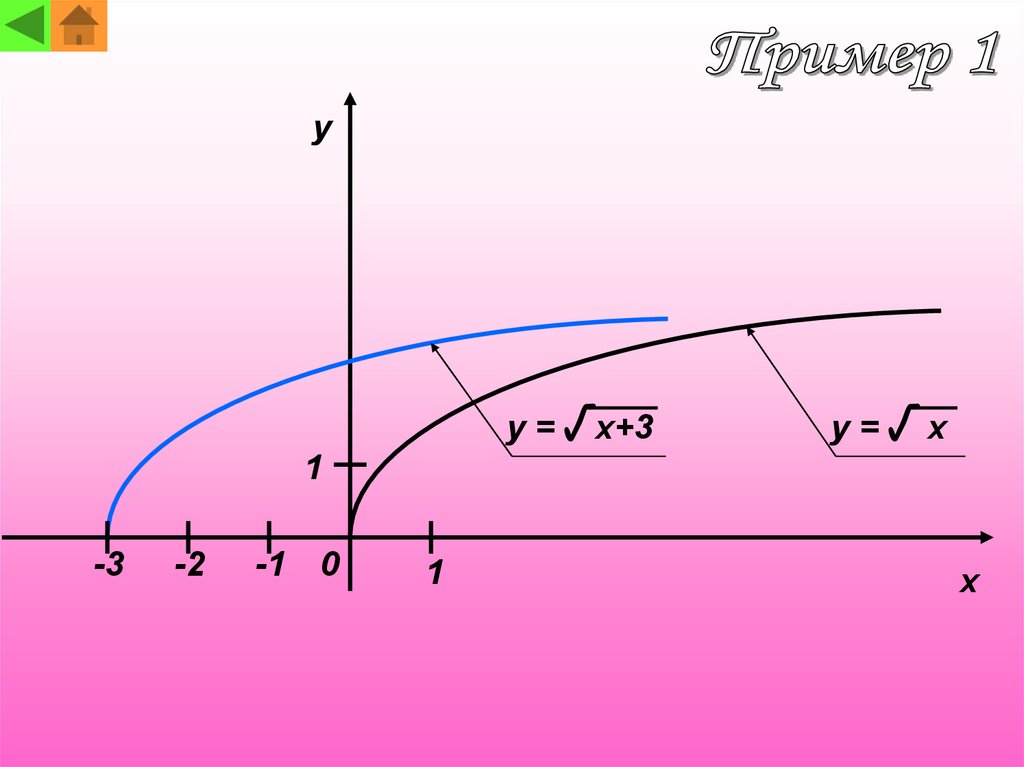
y
y = √ x+3
y=√ x
1
-3
-2
-1 0
1
x

11.

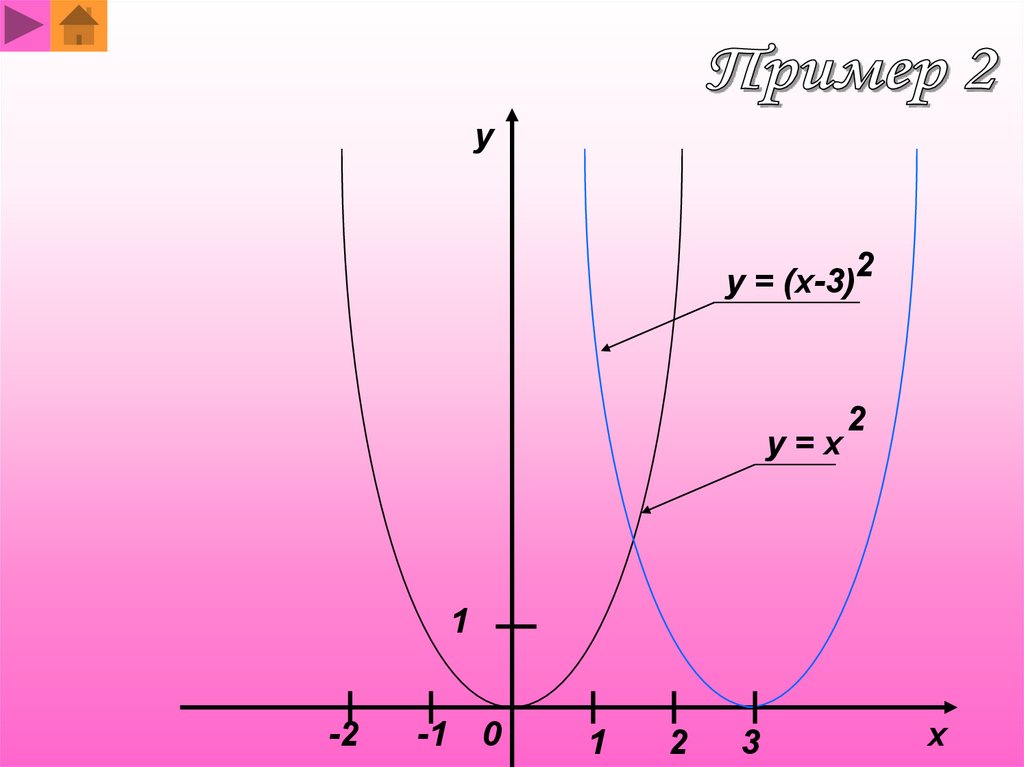
y
y = (x-3)2
y=x
2
1
-2
-1 0
1
2
3
x

12.

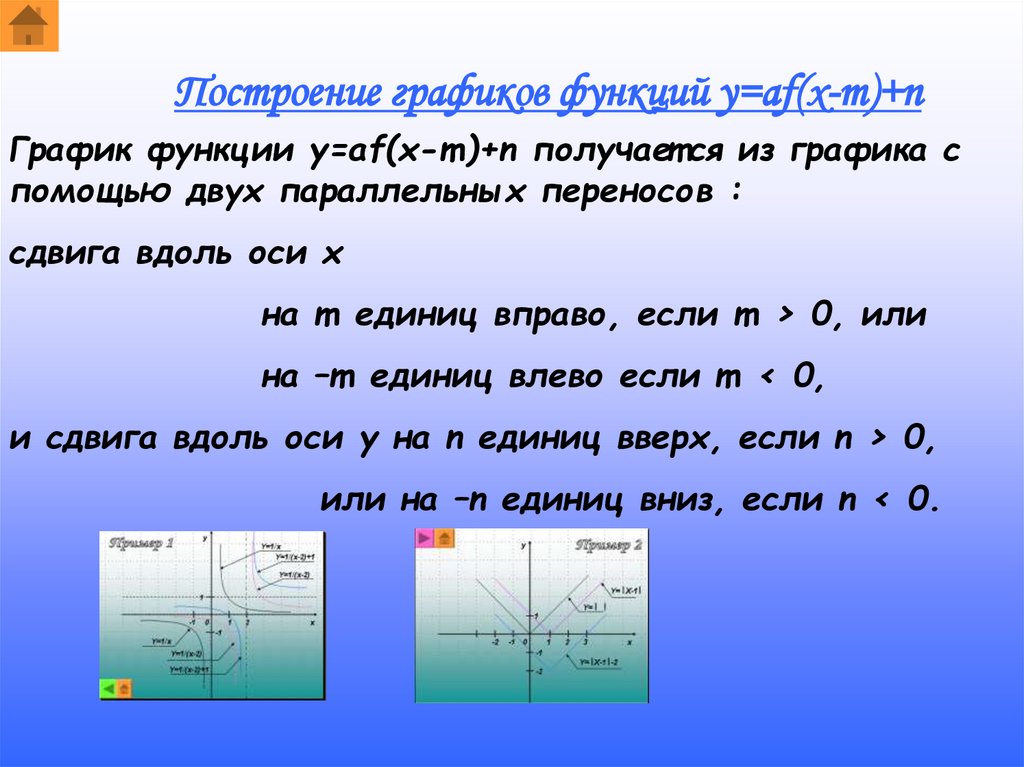
Построение графиков функций y=af(x-m)+n
График функции y=af(x-m)+n получает ся из графика с
помощью двух параллельных переносов :
сдвига вдоль оси x
на m единиц вправо, если m > 0, или
на –m единиц влево если m < 0,
и сдвига вдоль оси y на n единиц вверх, если n > 0,
или на –n единиц вниз, если n < 0.

13.

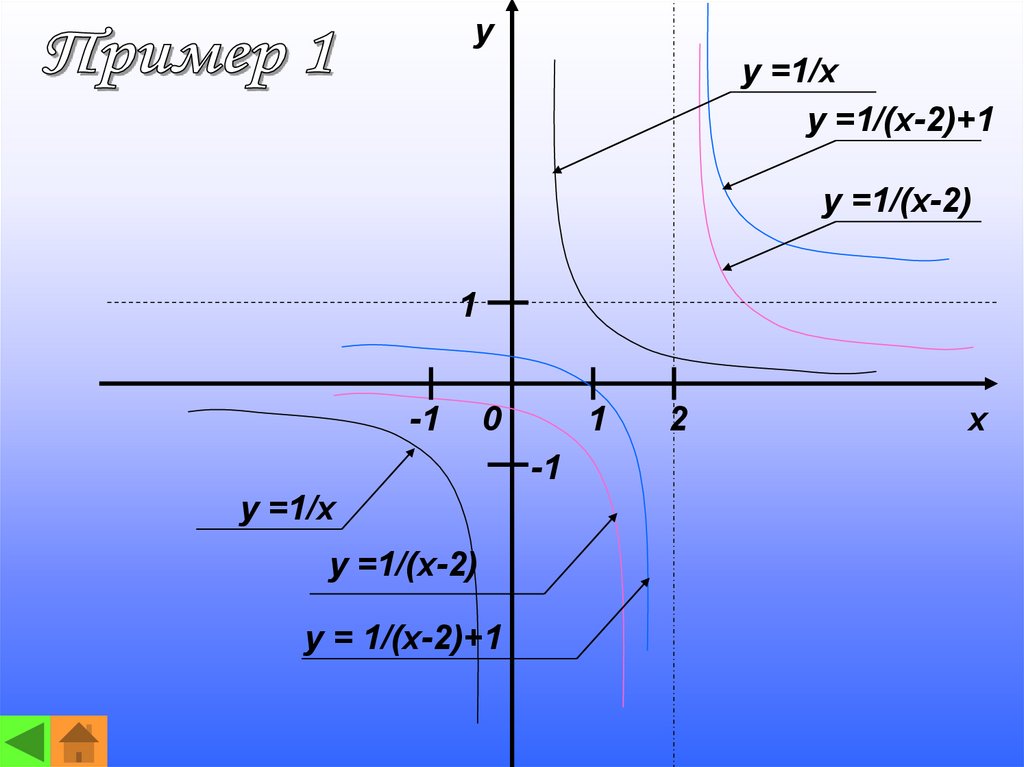
y
y =1/x
y =1/(x-2)+1
y =1/(x-2)
1
-1
0
1
-1
y =1/x
y =1/(x-2)
y = 1/(x-2)+1
2
x

14.

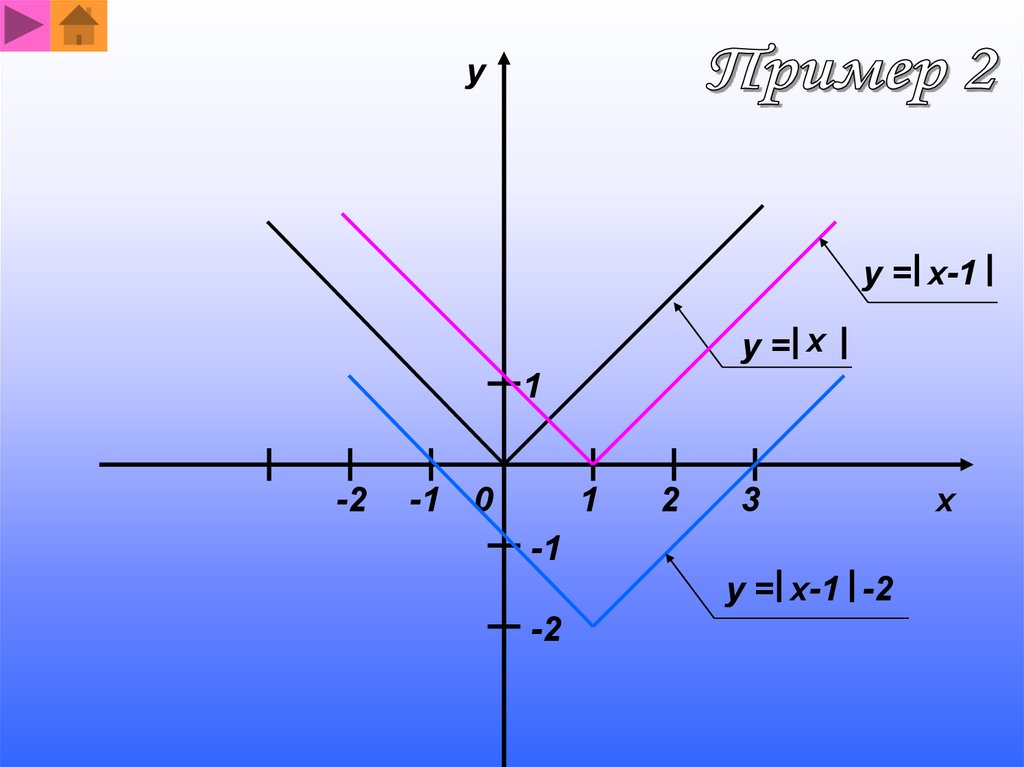
y
y = x-1
y= x
1
-2
-1 0
1
2
3
-1
y = x-1 -2
-2
x

15.

Другие примеры

16.

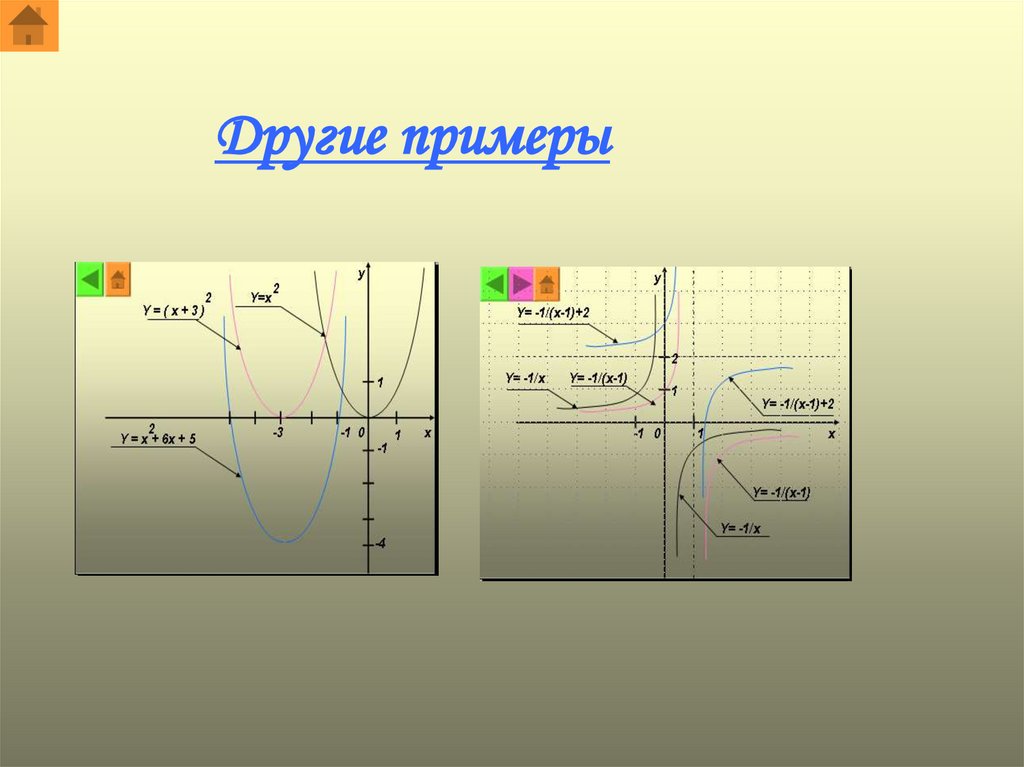
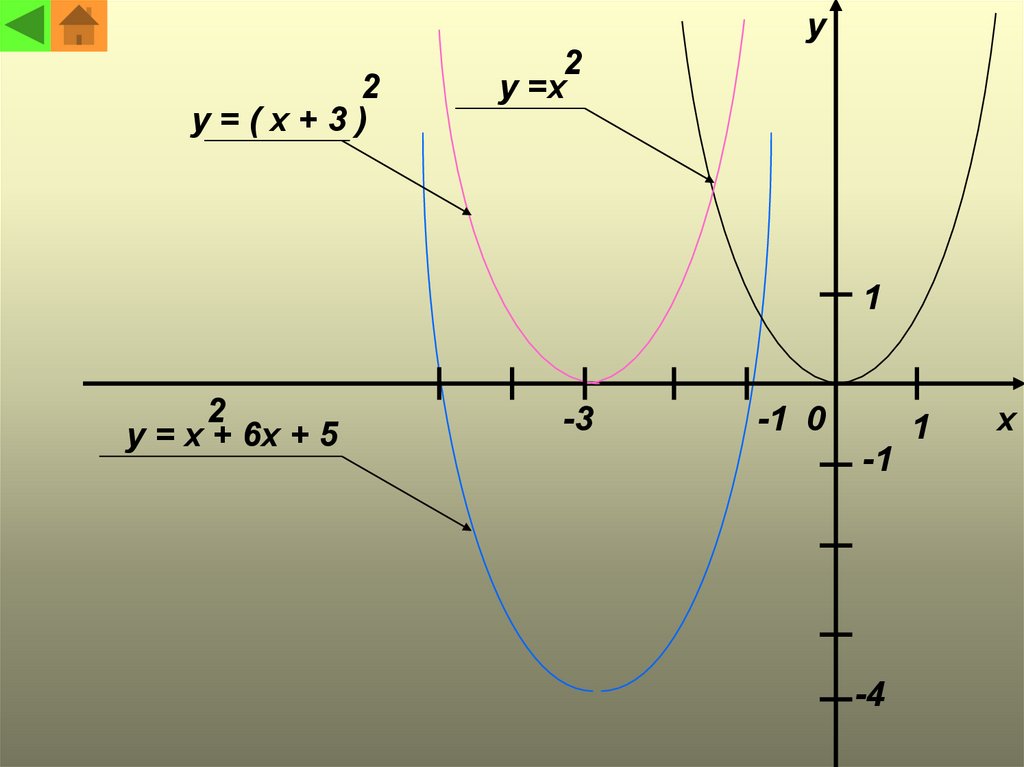
2
Построить график функции y = x + 6x + 5
Решение.
Преобразуем трехчлен, выделив в нем
полный квадрат.
2
2
2
y = ( x + 6x ) + 5 = ( x + 6x + 9 ) - 9 + 5 = ( x + 3 ) - 4

17.

y
2
y=(x+3)
2
y =x
1
2
y = x + 6x + 5
-3
-1 0
1
-1
-4
x

18.

3 - 2x
Построить график функции y = 1 - x
Решение.
В данной дробно-линейной функции выделим
целую часть.
( 2x – 2 ) - 1
3 - 2x
2x - 3
1
y=
=
=
=2
=
1-x
x-1
x-1
x-1
1
2
x-1

19.

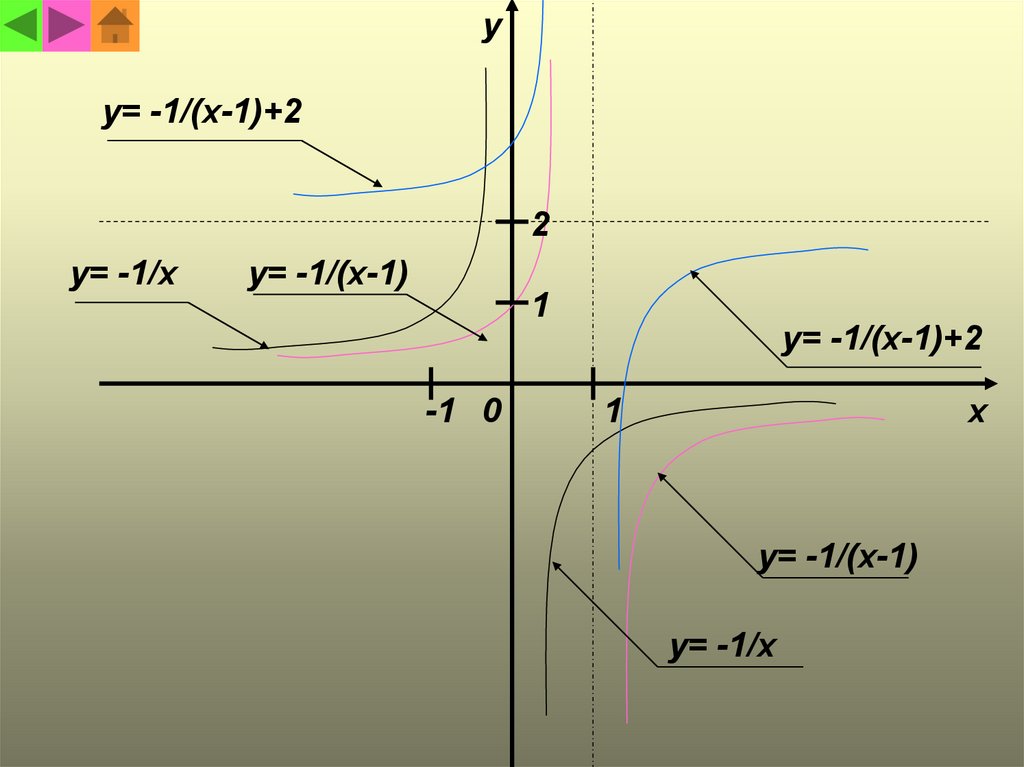
y
y= -1/(x-1)+2
2
y= -1/x
y= -1/(x-1)
1
y= -1/(x-1)+2
-1 0
1
x
y= -1/(x-1)
y= -1/x