Similar presentations:
Преобразование сумм тригонометрических функций в произведение
1. Преобразование сумм тригонометрических функций в произведение
Сумма (разность) синусовСумма (разность) косинусов
2. Рассмотрим выражение
sin s t sin s tsin s cos t cos s sin t sin s cos t cos s sin t
2 sin s cos t
sin s t sin s t 2 sin s cos t
3. Введем обозначения:
x s t,y s t
x y
x y 2s s
2
x y
x y 2t t
2
4. Тогда
Заменимs
на
s t на x , s t на
x y
x
y
, t на
2
2
y
ТОГДА
x y
x y
sin x sin y 2 sin
cos
2
2
5. Учитывая, что находим
Учитывая, что sin y sin yнаходим
sin x sin y sin x sin y
x y
x y
2 sin
cos
2
2
x y
x y
2 sin
cos
2
2
6. Получили формулу:
x yx y
sin x sin y 2 sin
cos
2
2
7.
Рассмотрим выражениеcos s t cos s t
cos s cos t sin s sin t cos s cos t sin s sin t
2 cos s cos t
cos s t cos s t 2 cos s cos t
8. Введем обозначения:
x s t, y s tПолучим:
x y
x y
cos x cos y 2 cos
cos
2
2
9.
Аналогично получаемx y
x y
cos x cos y 2 sin
sin
2
2

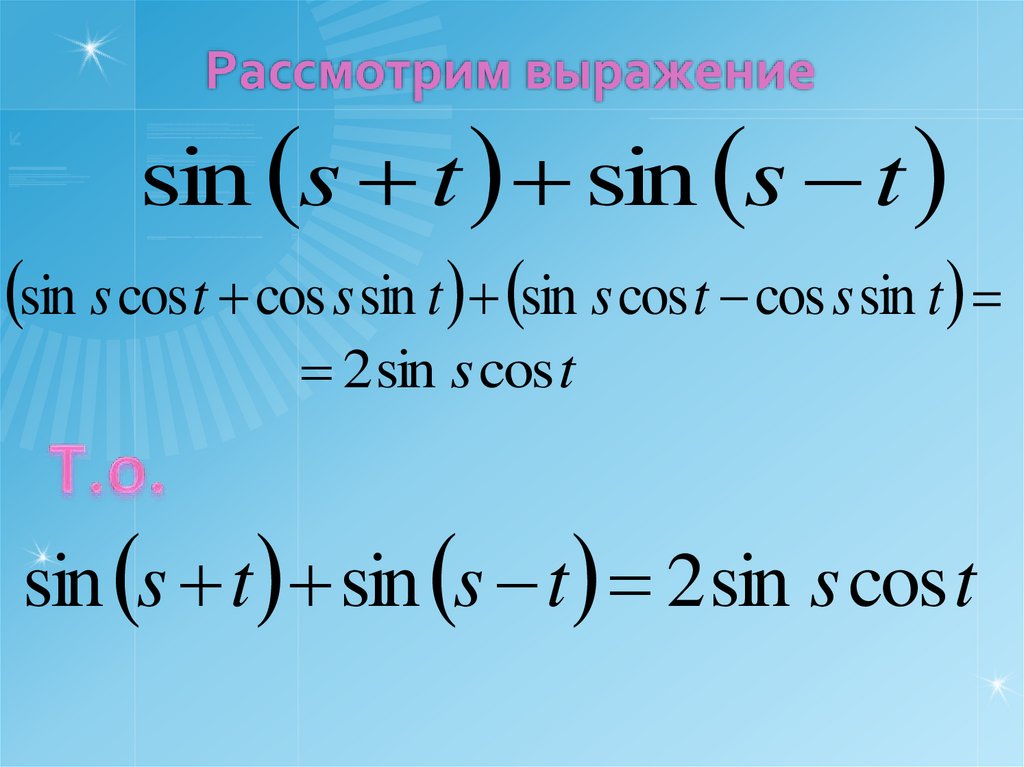




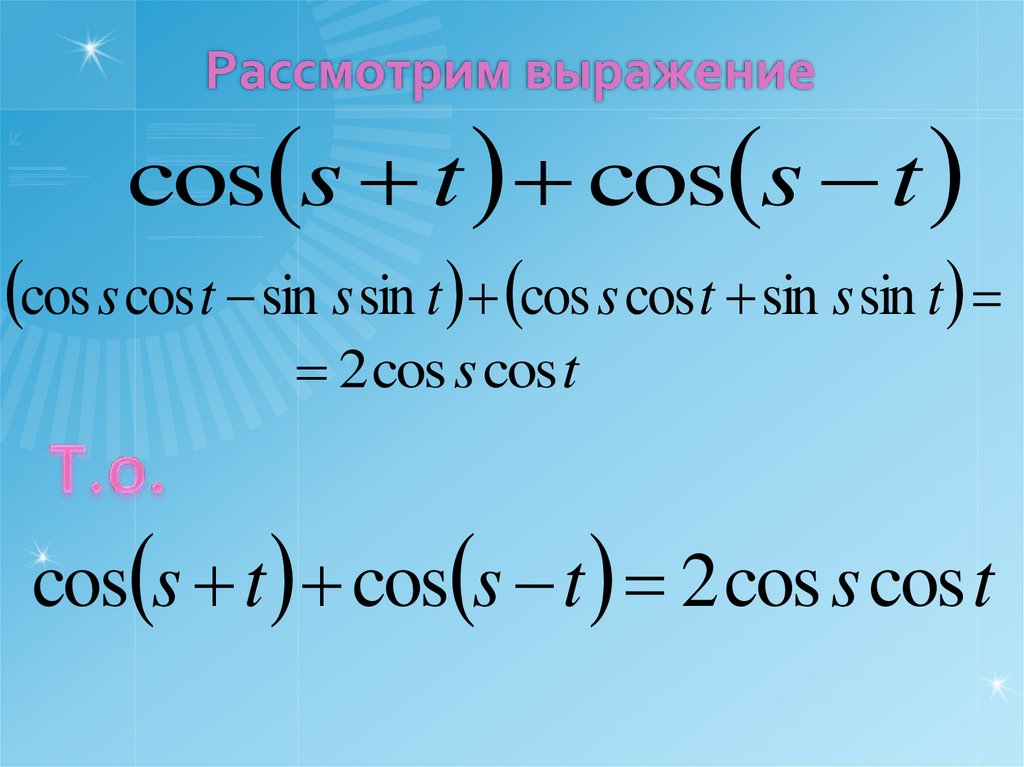


 mathematics
mathematics








