Similar presentations:
Квадратичная функция и её свойства
1.
Квадратичнаяфункция и её
свойства
2.
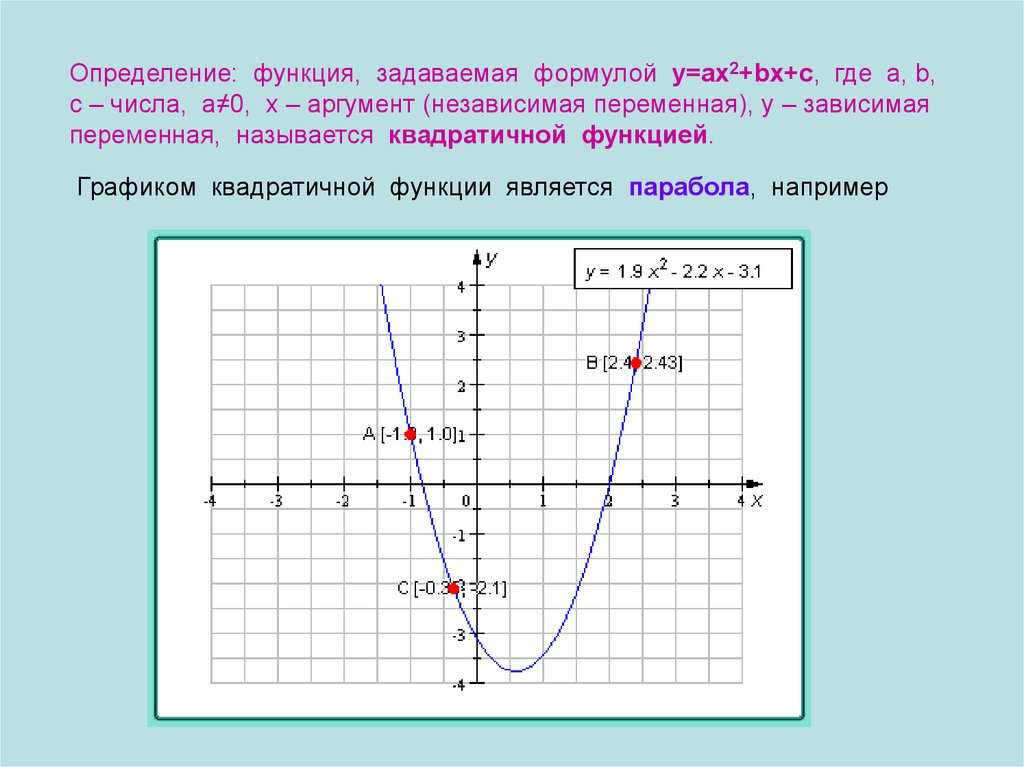
Определение: функция, задаваемая формулой у=ах2+bx+c, где а, b,c – числа, а≠0, х – аргумент (независимая переменная), у – зависимая
переменная, называется квадратичной функцией.
Графиком квадратичной функции является парабола, например
3.
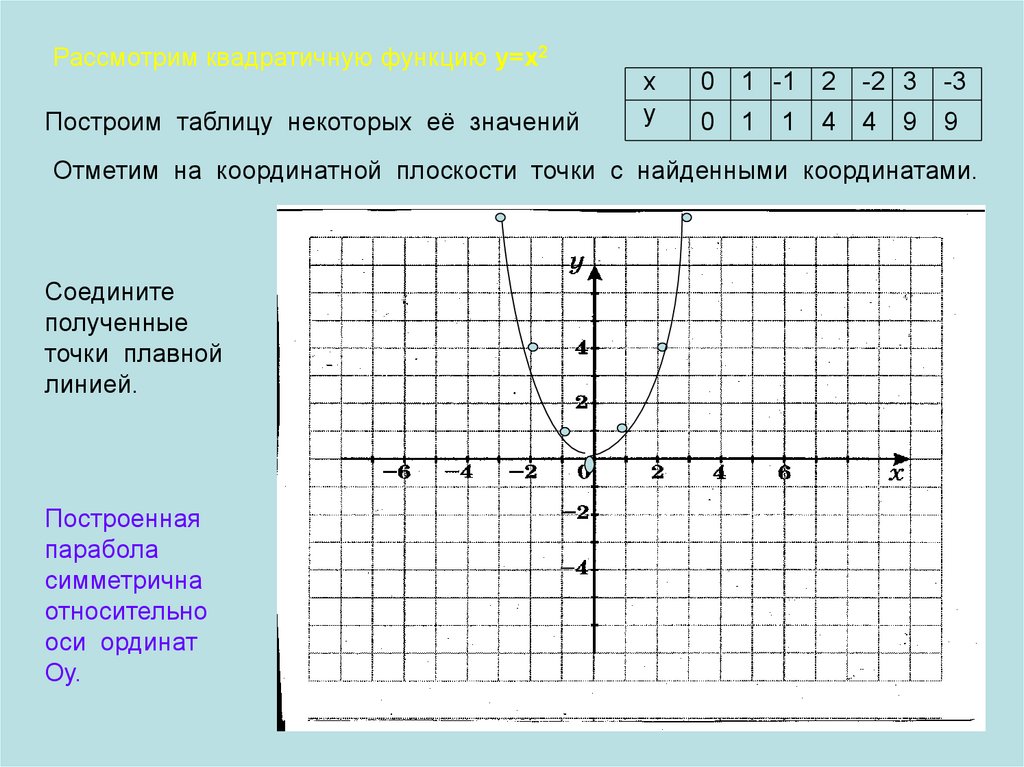
Рассмотрим квадратичную функцию у=х2Построим таблицу некоторых её значений
х
у
0
1 -1
2
-2 3
-3
0
1
4
4
9
1
9
Отметим на координатной плоскости точки с найденными координатами.
Соедините
полученные
точки плавной
линией.
Построенная
парабола
симметрична
относительно
оси ординат
Оу.
4.
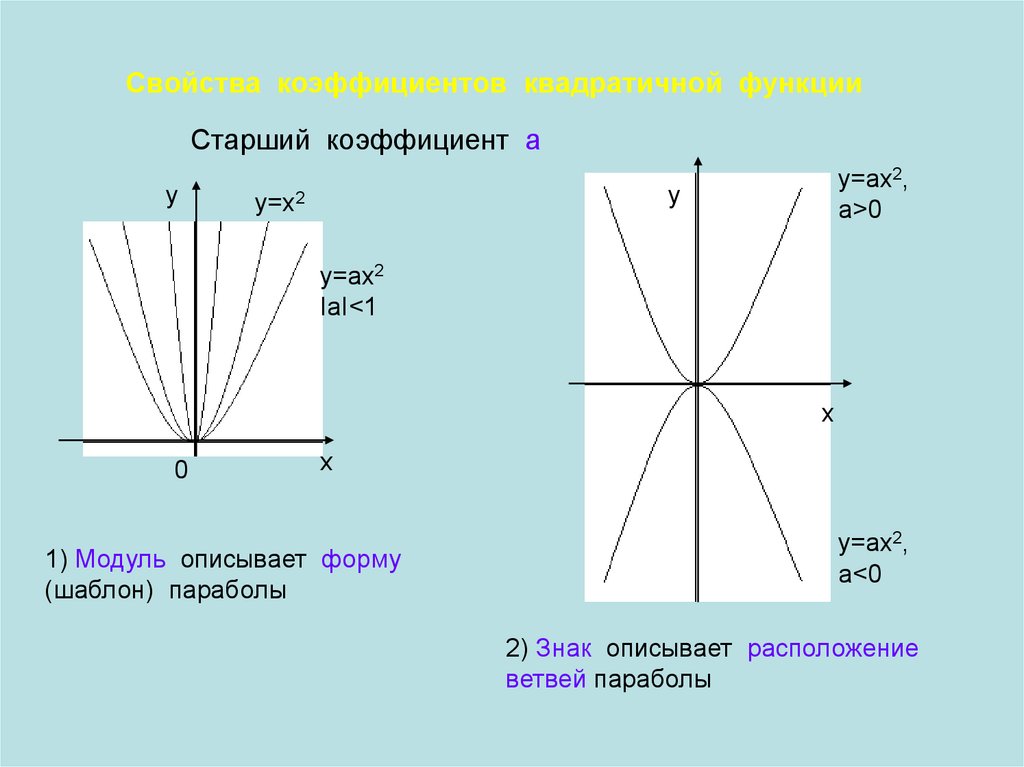
Свойства коэффициентов квадратичной функцииСтарший коэффициент a
у
y=ax2,
a>0
у
у=х2
y=ах2
IаI<1
х
0
х
1) Модуль описывает форму
(шаблон) параболы
y=ax2,
a<0
2) Знак описывает расположение
ветвей параболы
5.
Свойства коэффициентов квадратичной функцииСредний коэффициент b (коэффициент горизонтального сдвига)
Постройте две параболы у=х2+2х+1 и у=х2-2х+1
В них средние коэффициенты отличаются знаком
Составим таблицы значений
х
у
0
1
1
4
-1 2
0 9
х
0
1 -1
2
-2
3 -3
у
1
0
1
9
4 16
4
-2 3 -3
1 16 4
Получились две параболы
симметричные относительно
оси ординат Оу
6.
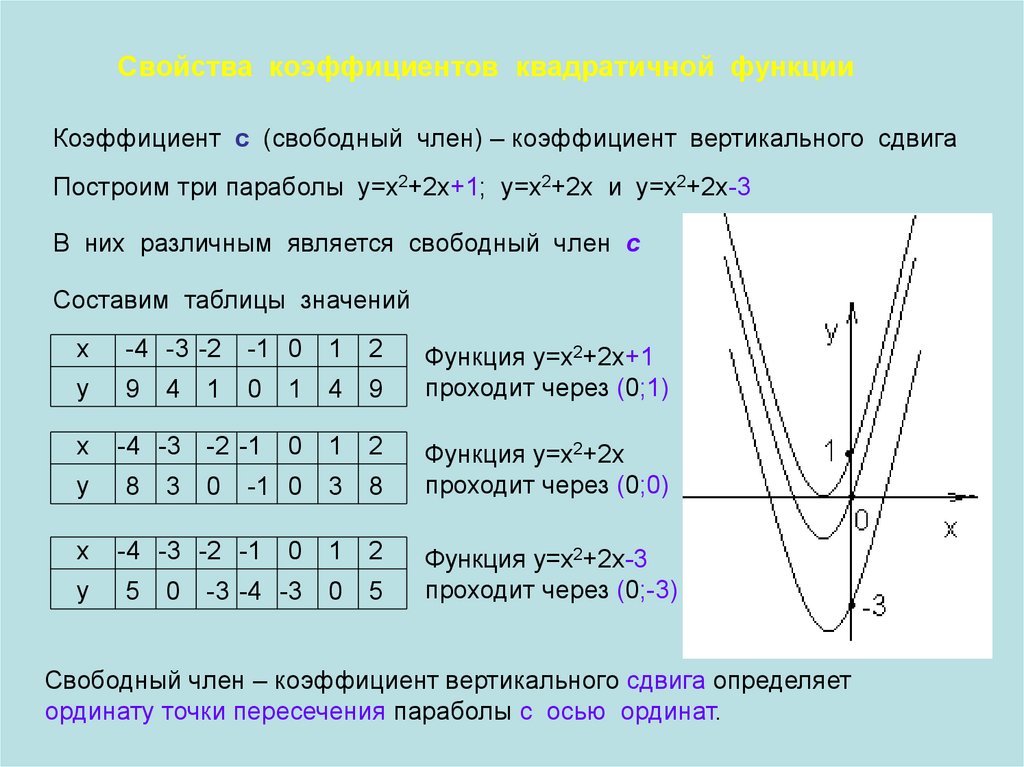
Свойства коэффициентов квадратичной функцииКоэффициент с (свободный член) – коэффициент вертикального сдвига
Построим три параболы у=х2+2х+1; у=х2+2х и у=х2+2х-3
В них различным является свободный член с
Составим таблицы значений
х
-4 -3 -2
-1 0
1
2
у
9
0
1
4
9
-4 -3 -2 -1
0
1
2
-1 0
3
8
0
1
2
-3 -4 -3
0
5
х
у
х
у
8
4
3
1
0
-4 -3 -2 -1
5
0
Функция у=х2+2х+1
проходит через (0;1)
Функция у=х2+2х
проходит через (0;0)
Функция у=х2+2х-3
проходит через (0;-3)
Свободный член – коэффициент вертикального сдвига определяет
ординату точки пересечения параболы с осью ординат.
7.
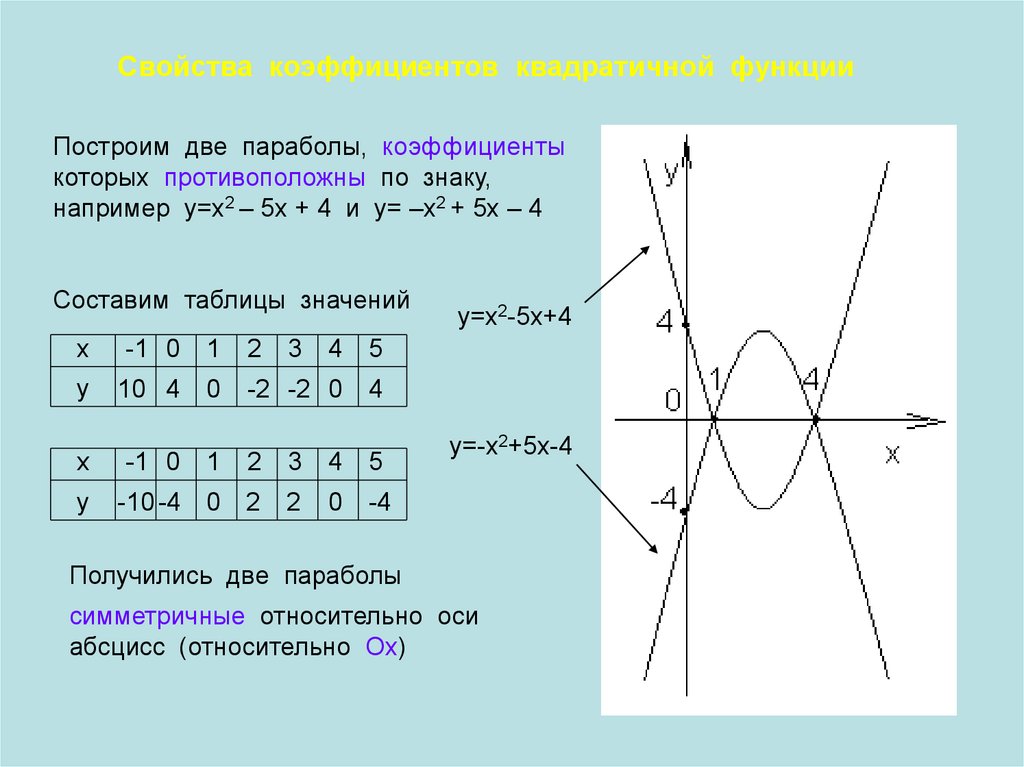
Свойства коэффициентов квадратичной функцииПостроим две параболы, коэффициенты
которых противоположны по знаку,
например у=х2 – 5х + 4 и у= –х2 + 5х – 4
Составим таблицы значений
х
-1 0
1
2
4
5
у
10 4
0
-2 -2 0
4
х
у
-1 0
1
3
2
3
4
5
-10 -4 0 2
2
0
-4
у=х2-5х+4
у=-х2+5х-4
Получились две параболы
симметричные относительно оси
абсцисс (относительно Ох)
8.
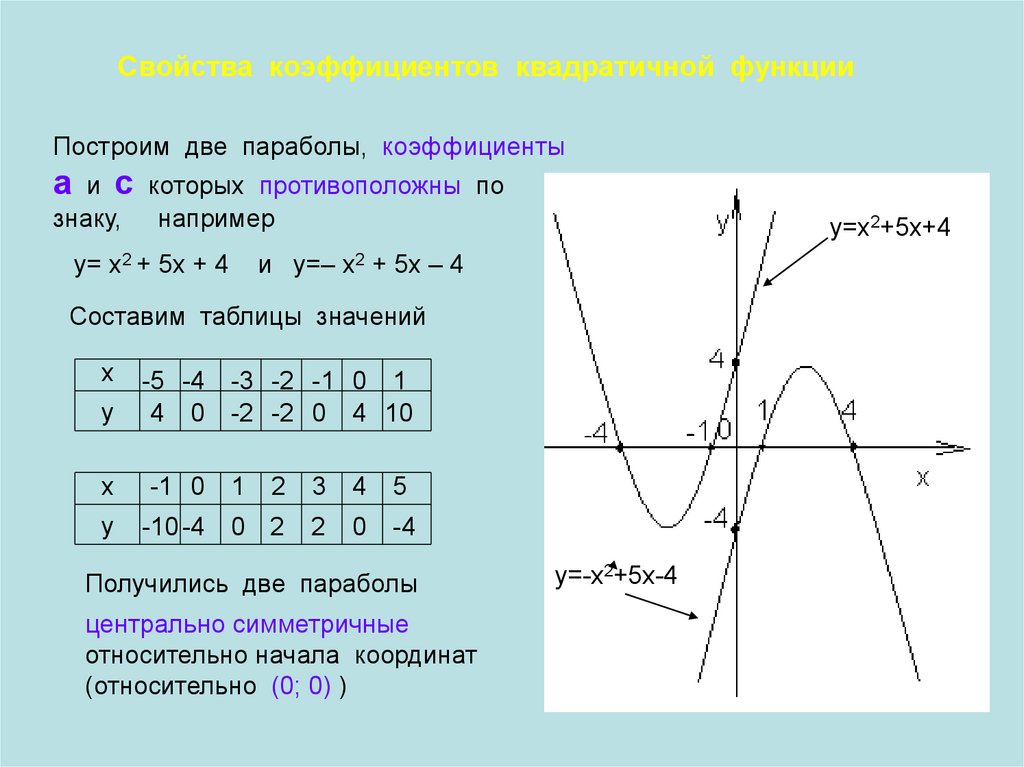
Свойства коэффициентов квадратичной функцииПостроим две параболы, коэффициенты
а
и с которых противоположны по
знаку, например
у= х2 + 5х + 4
у=х2+5х+4
и у=– х2 + 5х – 4
Составим таблицы значений
х
у
х
у
-5 -4 -3 -2 -1 0 1
4 0 -2 -2 0 4 10
-1 0
1
2
3
4
5
-10 -4 0 2
2
0
-4
Получились две параболы
центрально симметричные
относительно начала координат
(относительно (0; 0) )
у=-х2+5х-4
9.
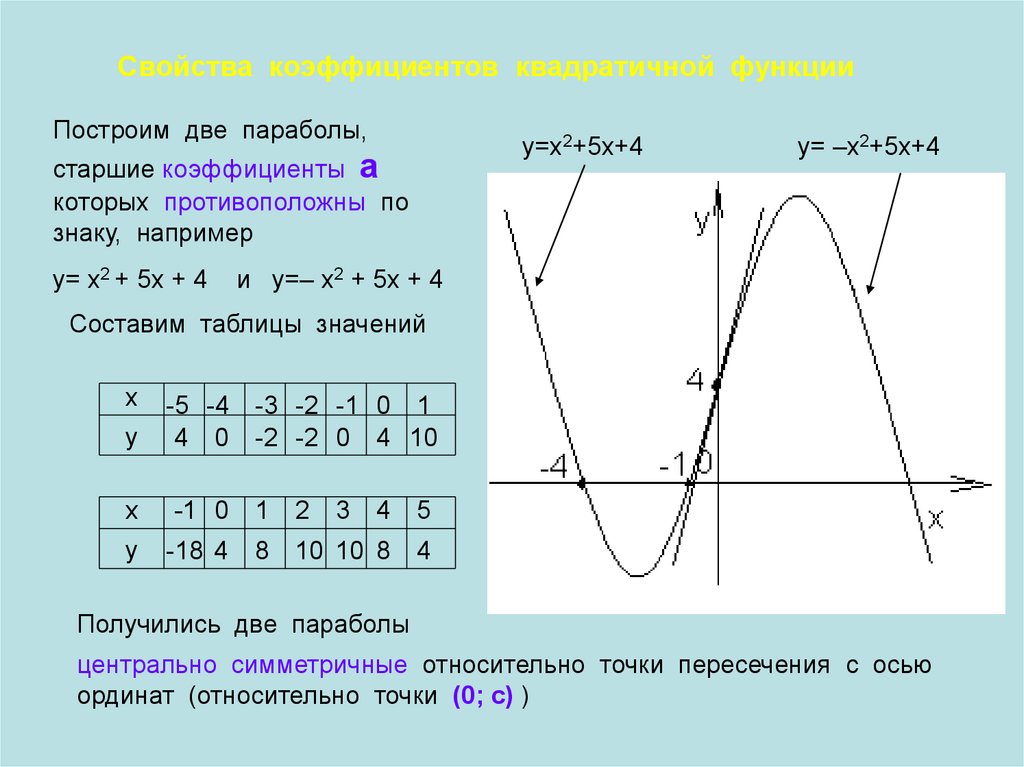
Свойства коэффициентов квадратичной функцииПостроим две параболы,
у=х2+5х+4
старшие коэффициенты а
которых противоположны по
знаку, например
у= х2 + 5х + 4
у= –х2+5х+4
и у=– х2 + 5х + 4
Составим таблицы значений
х
у
-5 -4 -3 -2 -1 0 1
4 0 -2 -2 0 4 10
х
-1 0
у
-18 4
1
2
3
4
5
8 10 10 8
4
Получились две параболы
центрально симметричные относительно точки пересечения с осью
ординат (относительно точки (0; с) )



 mathematics
mathematics








