Similar presentations:
Преобразования. Оконное преобразование Фурье. Области применения и ограничения оконного преобразования Фурье
1.
Фильтры, АЧХ которых равна единице навсех частотах, называются:
a) Фазовыми
b) Всепропускающими
c) Рекурсивными
d) Нерекурсивными
e) Адаптивными
1
2. Преобразования Оконное преобразование Фурье. Области применения и ограничения оконного преобразования Фурье.
Вейвлет-преобразования:Масштабирующие функции. Ортогональное,
непрерывное и дискретное вейвлетпреобразование.
3. Преобразования
Пусть f(t) – сигнал непрерывного времени.Тогда его преобразование в общем виде можно
представить:











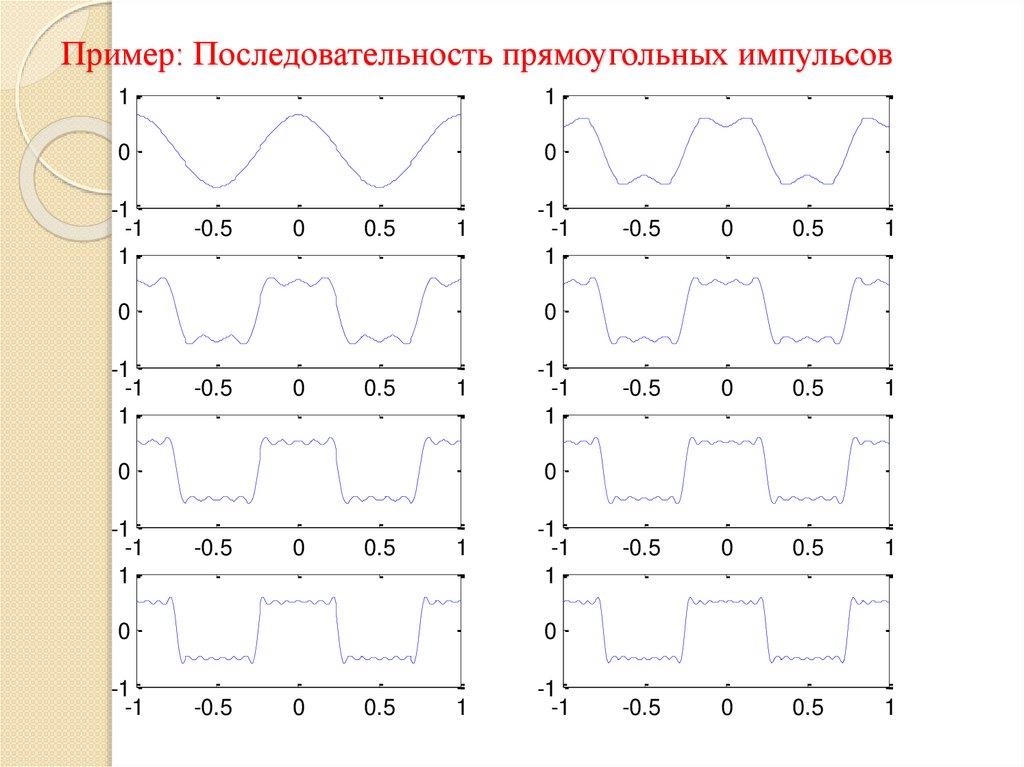


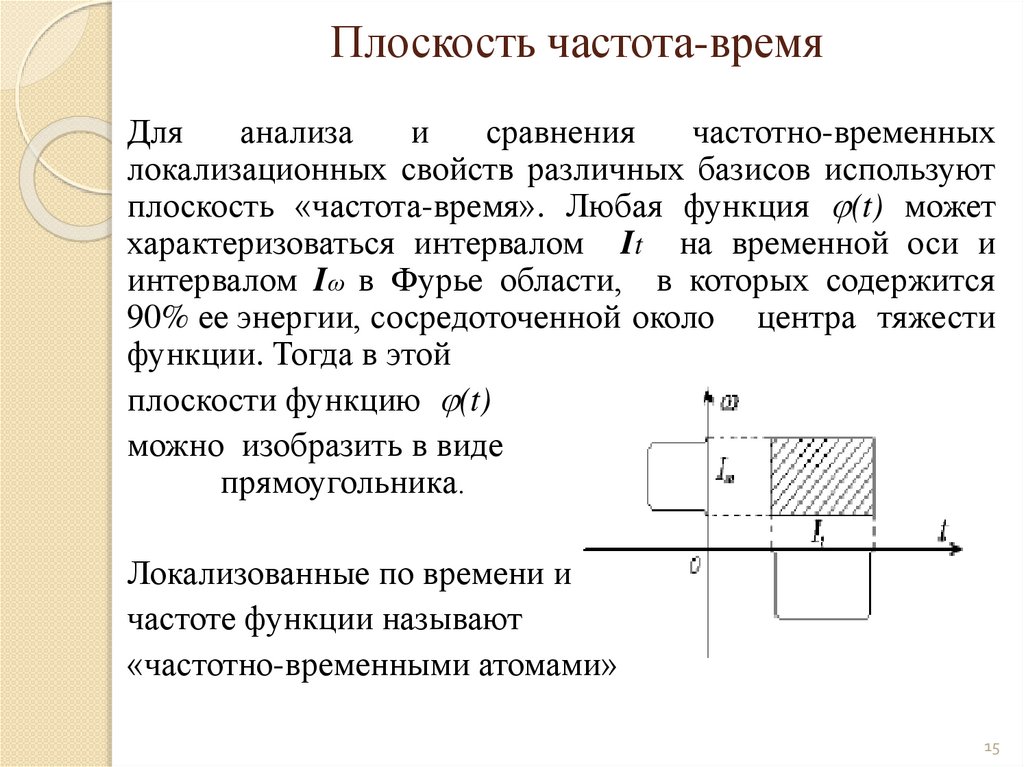
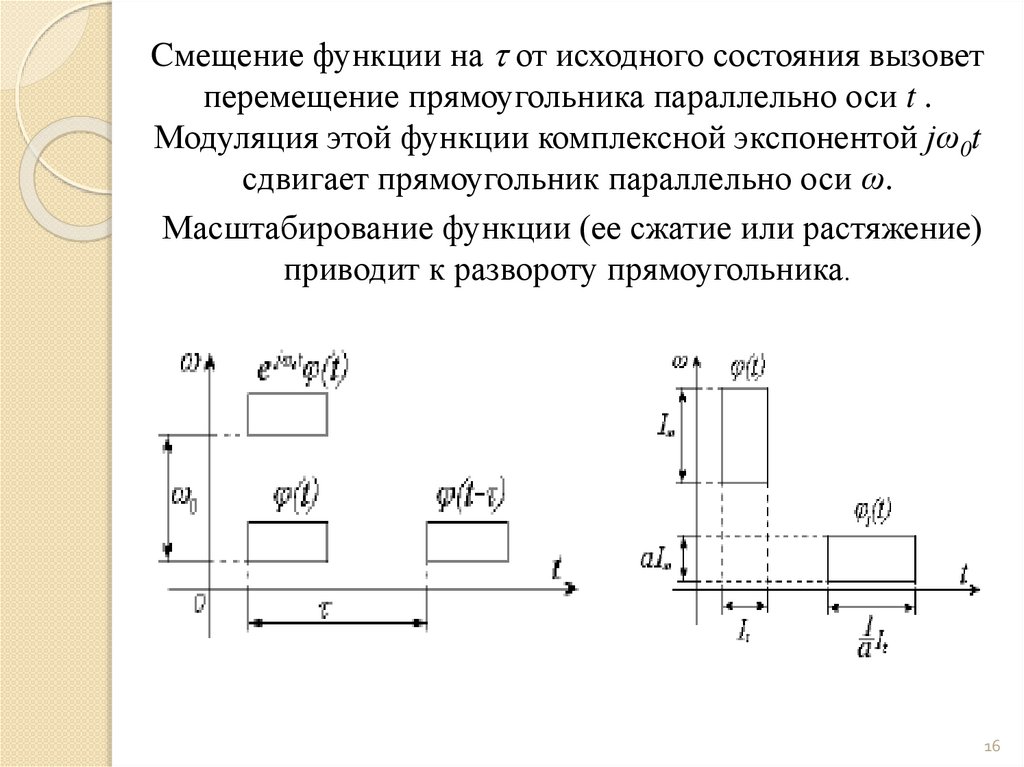
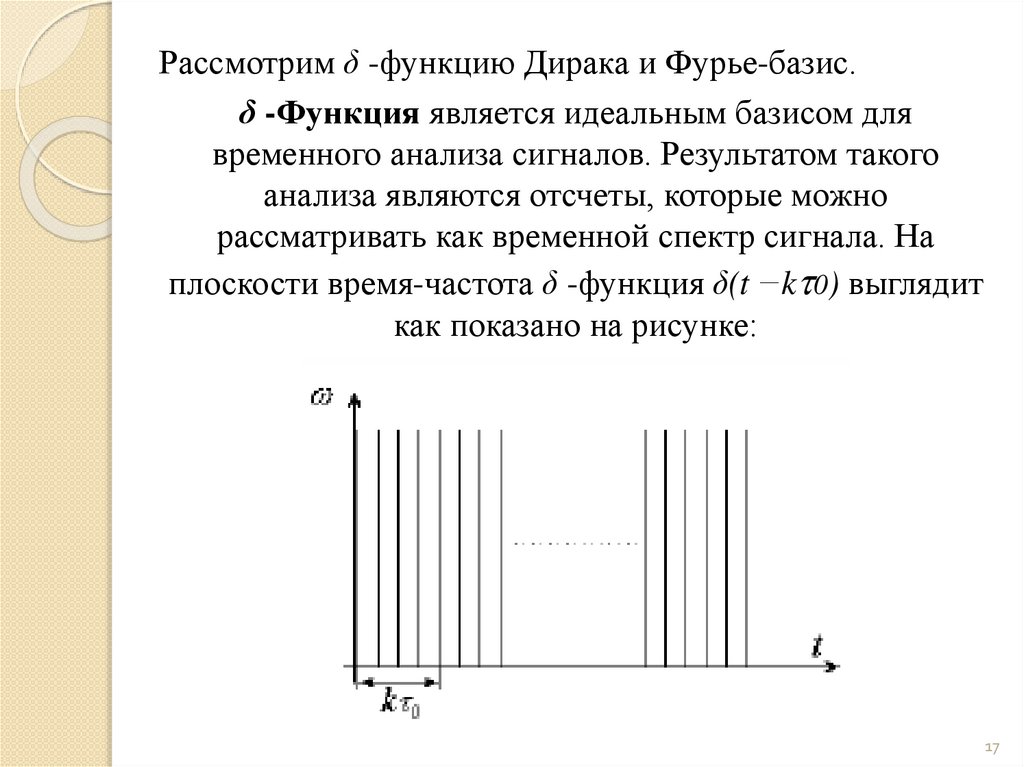



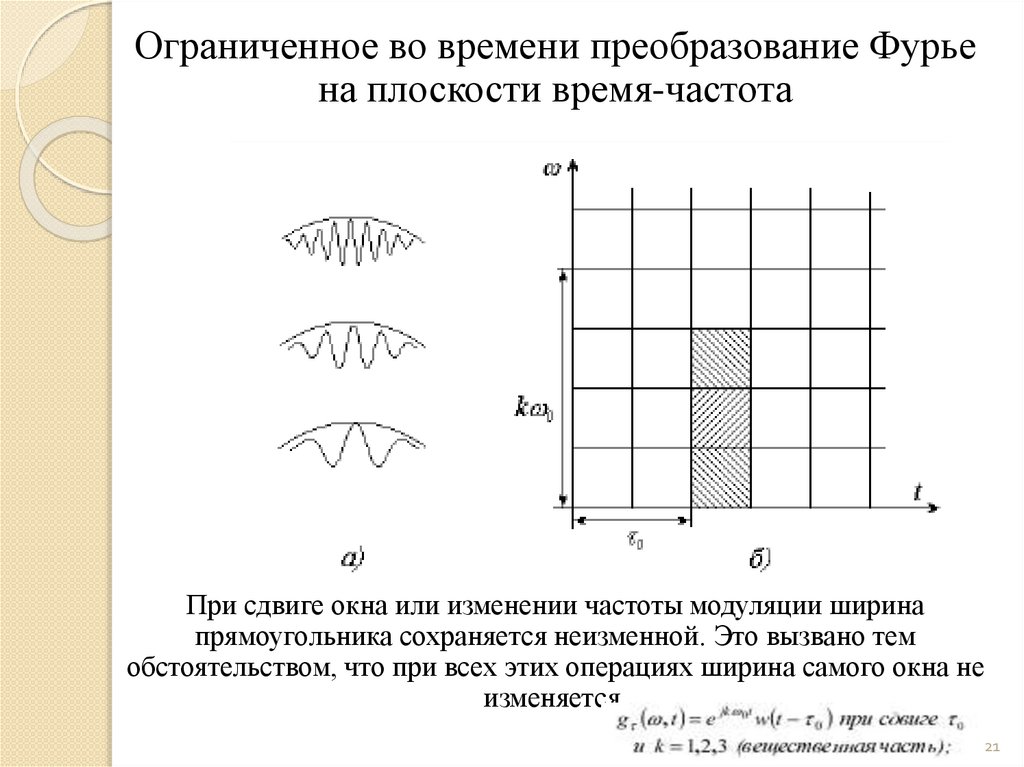



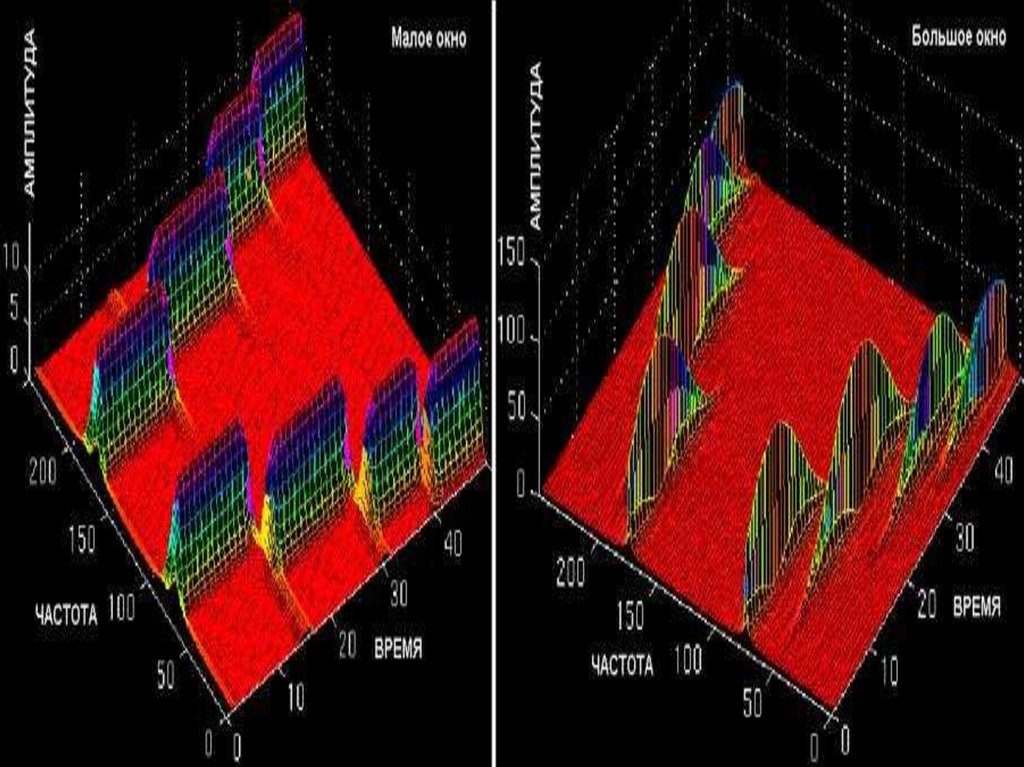






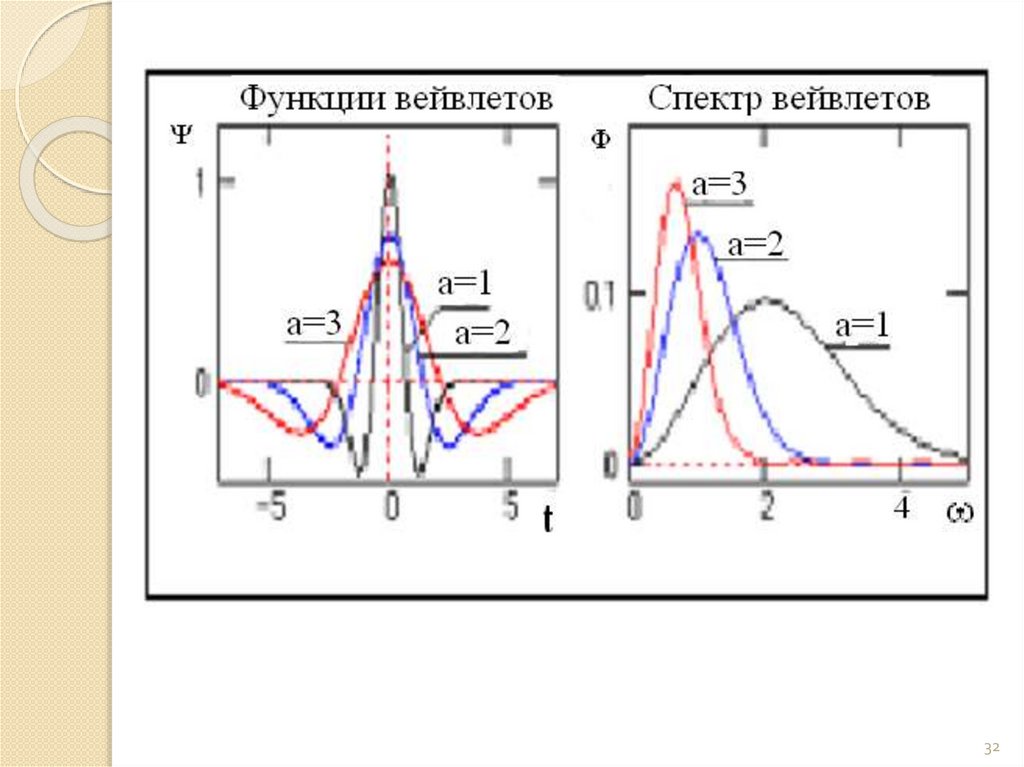



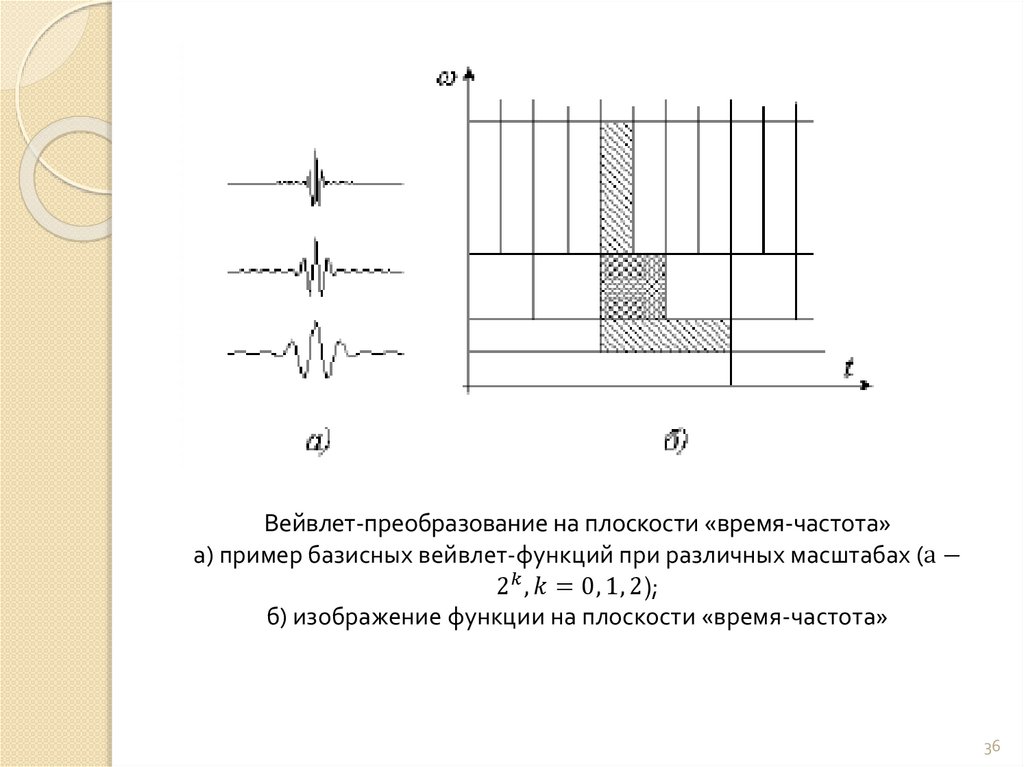

























 mathematics
mathematics








