Тригонометрические неравенства

1.

2
Линейное неравенство sin x
2
y
1.
2
На Оу отмечаем значение
0 ,7
2
и соответствующие точки на
окружности.
2
5
4
2
2
4
2
2.
Выделяем нижнюю часть
окружности (обход совершаем
против часовой стрелки).
3.
17.08.16
Подписываем полученные точки. Обязательно
учитываем, что начало дуги – меньшее значение.
x
5
2 k ; 2 k
4. Ответ: х
4
4
1

2.

2
Линейное неравенство cos x
2
y
1.
2.
2
0 ,7
2
и соответствующие точки на
окружности.
2
На Ох отмечаем значение
Выделяем правую часть
окружности (обход совершаем
против часовой стрелки).
3
4
2
2
2
x
3.
17.08.16
3
4
Подписываем полученные точки. Обязательно
учитываем, что начало дуги – меньшее значение.
3
3
2 k ;
2 k
4. Ответ: х
4
4
2

3.

3
Линейное неравенство sin x
2
y
3
0 ,8
2
и соответствующие точки на
окружности.
2
2. Выделяем верхнюю часть
окружности (обход совершаем
против часовой стрелки).
1.
На Оу отмечаем значение
2
x
4
3
3.
17.08.16
3
2
3
Подписываем полученные точки. Обязательно
учитываем, что начало дуги – меньшее значение.
4
2 k ;
2 k
4. Ответ: х
3
3
3

4.

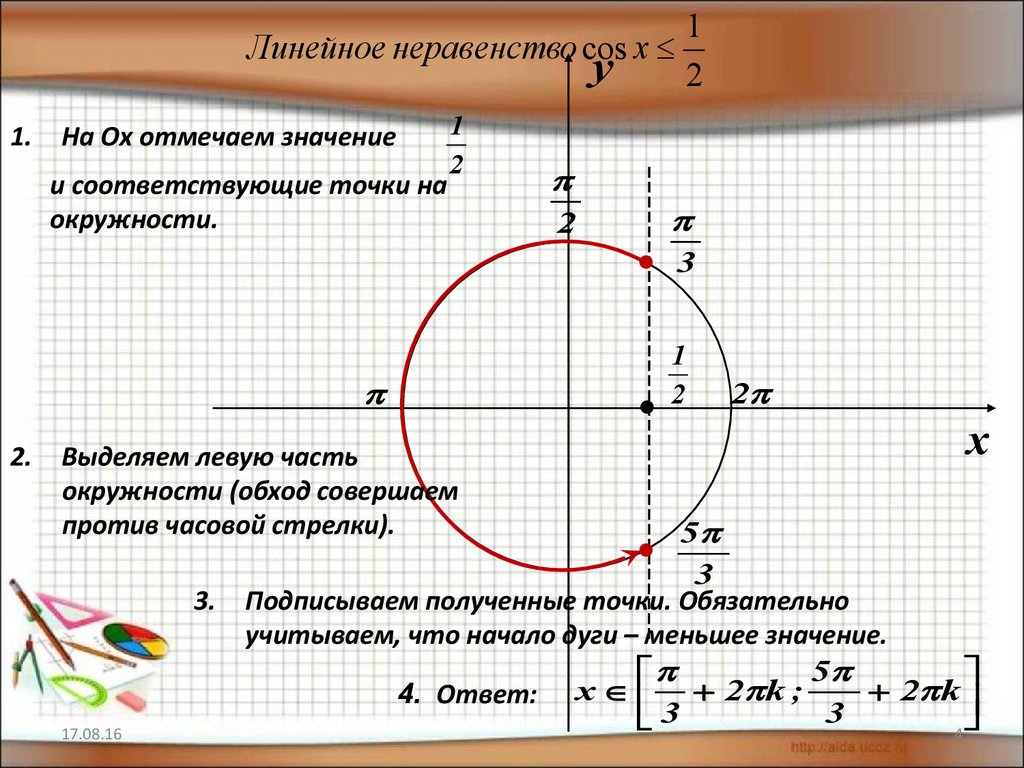
1
Линейное неравенство cos x
y
2
1.
На Оx отмечаем значение
и соответствующие точки на
окружности.
1
2
2
3
2.
1
2
2
x
Выделяем левую часть
окружности (обход совершаем
против часовой стрелки).
17.08.16
5
3
3. Подписываем полученные точки. Обязательно
учитываем, что начало дуги – меньшее значение.
5
2 k
4. Ответ: х 2 k ;
3
3
4

5.

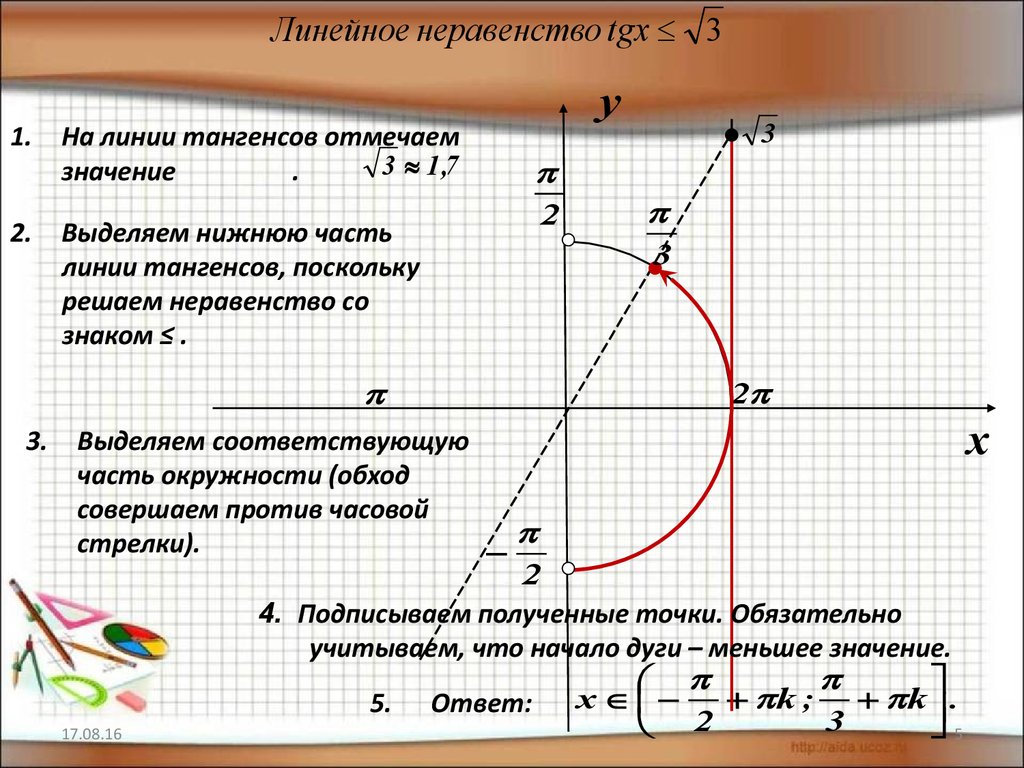
Линейное неравенство tgx 3
1.
На линии тангенсов отмечаем
3 1 ,7
значение
.
2.
Выделяем нижнюю часть
линии тангенсов, поскольку
решаем неравенство со
знаком ≤ .
y
3.
Выделяем соответствующую
часть окружности (обход
совершаем против часовой
стрелки).
17.08.16
3
2
3
2
2
4. Подписываем полученные точки. Обязательно
учитываем, что начало дуги – меньшее значение.
х
k
;
k
.
5. Ответ:
3
2
5
x

6.

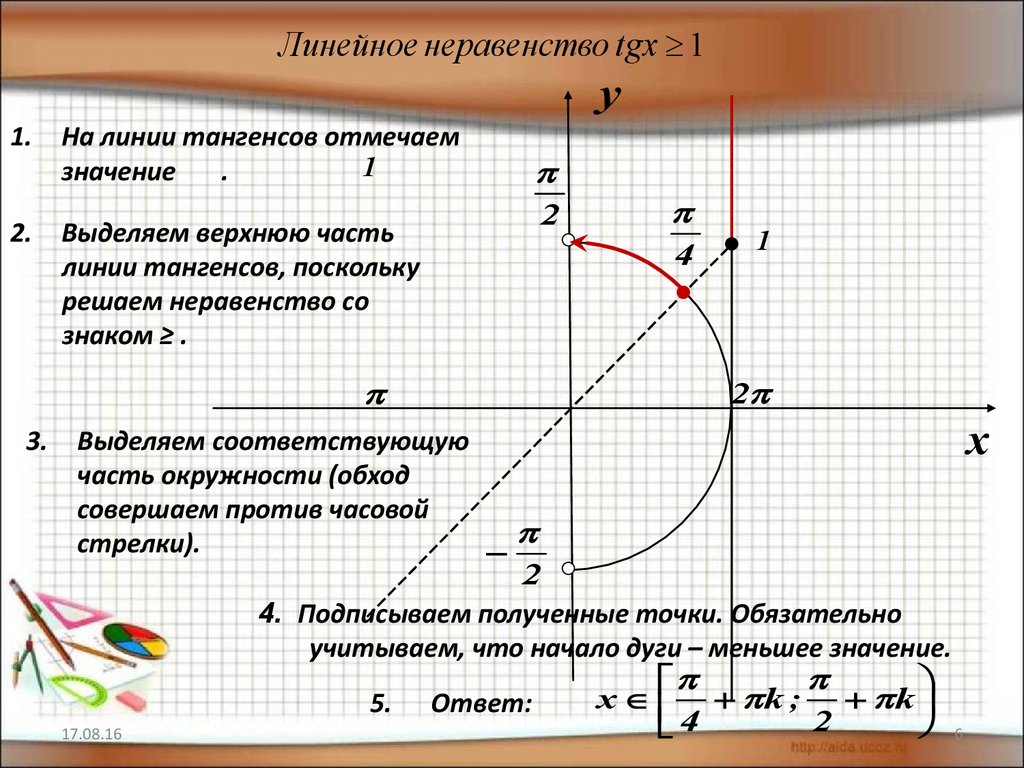
Линейное неравенство tgx 1
y
1.
На линии тангенсов отмечаем
1
значение
.
2.
Выделяем верхнюю часть
линии тангенсов, поскольку
решаем неравенство со
знаком ≥ .
3.
Выделяем соответствующую
часть окружности (обход
совершаем против часовой
стрелки).
17.08.16
2
4
1
2
2
4. Подписываем полученные точки. Обязательно
учитываем, что начало дуги – меньшее значение.
х
k
;
k
5. Ответ:
4
2
6
x

7. Квадратное неравенство

Обозначим sinx =t и получим квадратное неравенство
решение которого есть
t < 1/2 и t > 2,
Отсюда следует совокупность неравенств sinx > 2,
sinx < 1/2,
Первое неравенство совокупности решений не имеет, а из
второго получим
• Ответ:
17.08.16
7

8. Однородное неравенство sin x + cos x ≤0

sin x + cos x ≤0
приравняем sin x + cos x =0 / :cosx
tgx+1=0
tgx=-1
x=3 π /4+ π n
???
17.08.16
8

9. Однородное неравенство cosx+sinx≥0 1)разделим на cosx 2)рассмотрим 2 случая

1сл cosx >0
tgx ≥-1
x ≥ 3π/4+ πn, n Є Z
x> π/2+ πn, n Є Z
x Є[3π/4+2 πn; 3π/2, n Є Z]
2сл cosx<0
tgx≤0
x ≥ π/4+ πn, n Є Z
x> π/2+ πn, n Є Z
x Є[π/4+2 πn; π/2, n Є Z]

10.

Спасибо за внимание!