Similar presentations:
Решение простейших тригонометрических неравенств
1. Решение простейших тригонометрических неравенств
20.12.20231
2.
2sin x
2
1.
2
На Оу отмечаем значение
0 ,7
2
и соответствующие точки на
окружности.
2
5
4
2.
y
2
2
4
2
x
Выделяем нижнюю часть
окружности (обход совершаем
против часовой стрелки).
3.
Подписываем полученные точки. Обязательно
учитываем, что начало дуги – меньшее значение.
4. Ответ:
20.12.2023
5
х
2 k ; 2 k k
4
4
2
3.
2cos x
2 y
1.
2.
На Ох отмечаем значение 2 0 ,7
2
и соответствующие точки на
окружности.
2
Выделяем правую часть
окружности (обход совершаем
против часовой стрелки).
3
4
2
2
3.
20.12.2023
2
x
3
4
Подписываем полученные точки. Обязательно
учитываем, что начало дуги – меньшее значение.
4. Ответ: х 3 2 k ; 3 2 k k
4
4
3
4.
3sin x
2 y
3
0,8
2
и соответствующие точки на
окружности.
2
2. Выделяем верхнюю часть
окружности (обход совершаем
против часовой стрелки).
1.
На Оу отмечаем значение
2
x
4
3
3.
20.12.2023
3
2
3
Подписываем полученные точки. Обязательно
учитываем, что начало дуги – меньшее значение.
4
х
2
k
;
2
k
k
4. Ответ:
3
3
4
5.
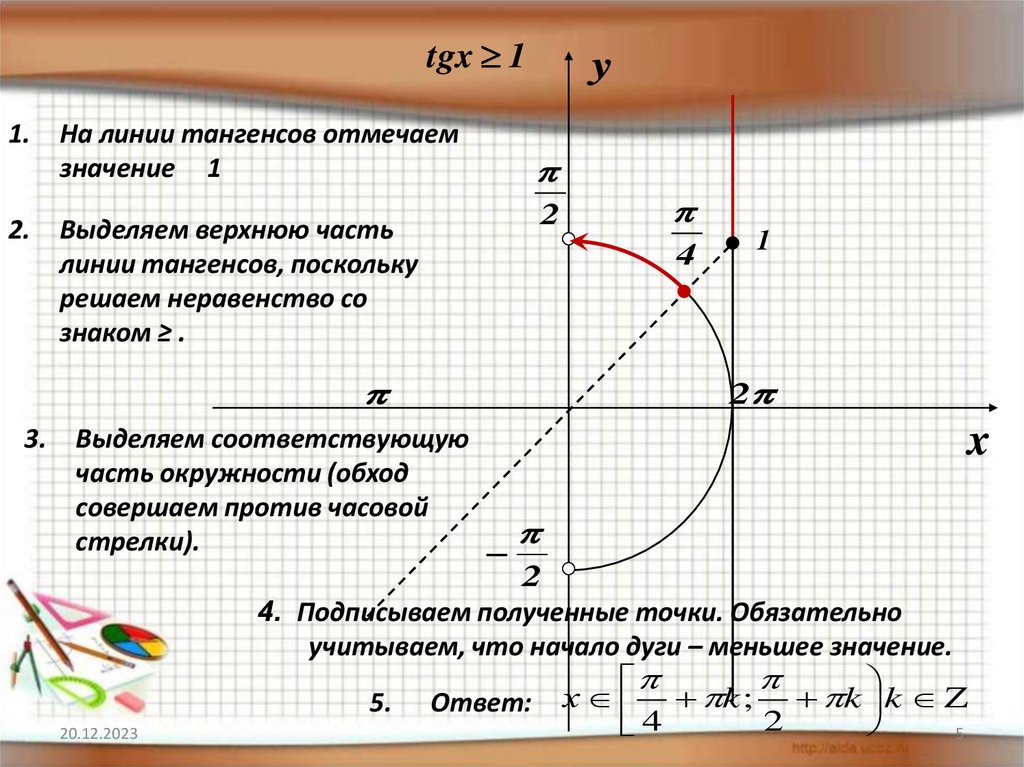
tgx 11.
На линии тангенсов отмечаем
значение 1
2.
Выделяем верхнюю часть
линии тангенсов, поскольку
решаем неравенство со
знаком ≥ .
y
2
4
1
2
3.
Выделяем соответствующую
часть окружности (обход
совершаем против часовой
стрелки).
x
2
20.12.2023
4. Подписываем полученные точки. Обязательно
учитываем, что начало дуги – меньшее значение.
5. Ответ: х k ; k k
2
4
5
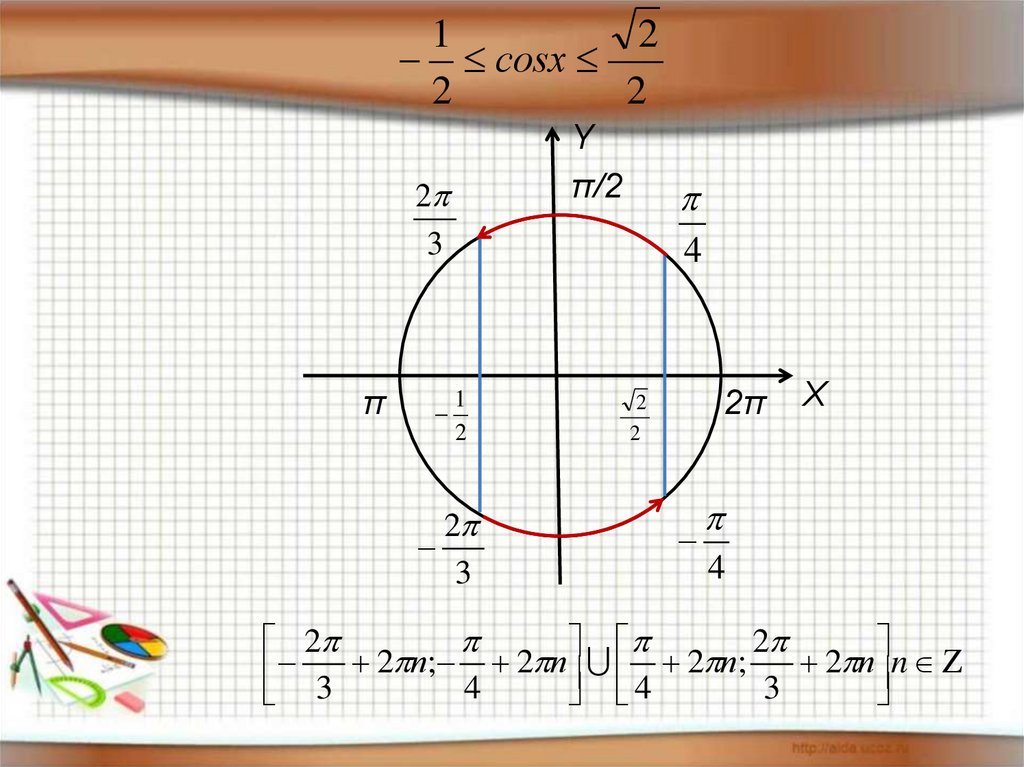
6.
12
соsx
2
2
Y
π/2
2
3
π
1
2
2
3
4
2π
2
2
X
4
2
2
3 2 п; 4 2 п 4 2 п; 3 2 п n
7.
Попробуйте каждый придуматьи решить своё неравенство
по этой теме на оценку.





 mathematics
mathematics








