Similar presentations:
Дүниенің сәнін екі нәрсе келтіреді
1. Қазіргі заманда жастарға ақпараттық технологиямен байланысты әлемдік стандартқа сай мүдделі жаңа білім беру өте қажет Н.Ә.
әлемдікстандартқа сай
мүдделі жаңа
білім беру өте
қажет
Н.Ә.
Назарбаев
Дүниенің сәнін екі нәрсе келтіреді:
Бірі - математикамен шұғылдану,
екіншісі - одан сабақ беру
С.Д. Пуассон
2. Матрицалар және оларға амалдар қолдану
Панорамалық сабақ3.
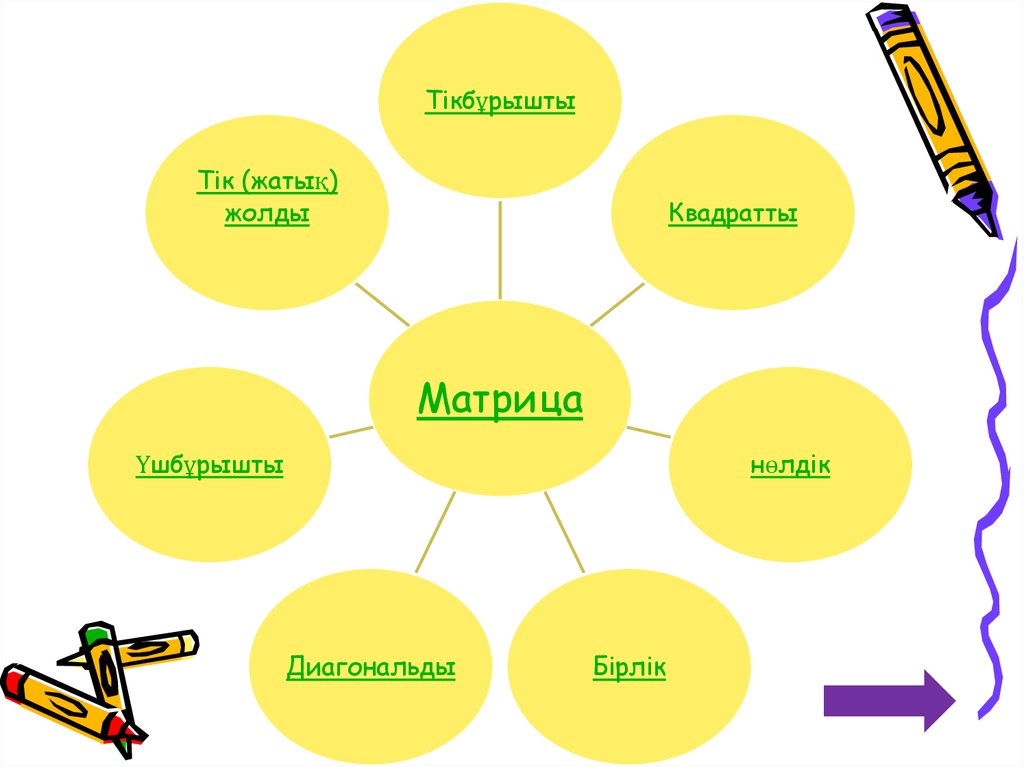
ТікбұрыштыТік (жатық)
жолды
Квадратты
Матрица
нөлдік
Үшбұрышты
Диагональды
Бірлік
4.
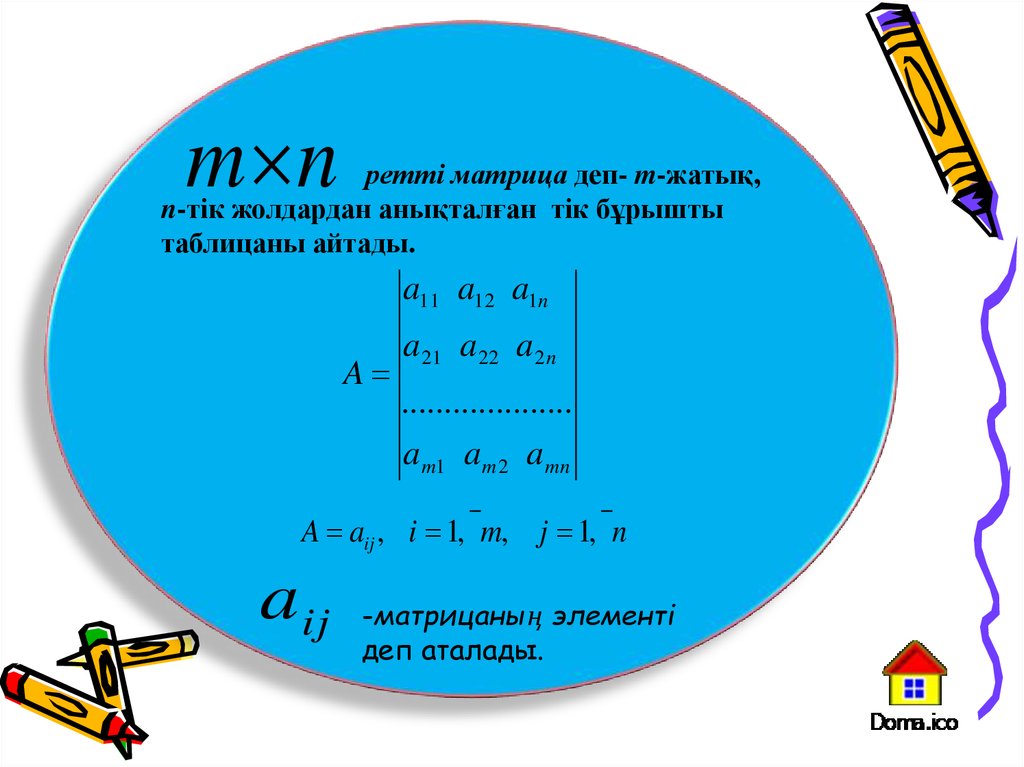
m nретті матрица деп- m-жатық,
n-тік жолдардан анықталған тік бұрышты
таблицаны айтады.
a11 a12 a1n
A
a 21 a 22 a 2 n
....................
a m1 a m 2 a mn
A aij , i 1, m, j 1, n
a ij
-матрицаның элементі
деп аталады.
5.
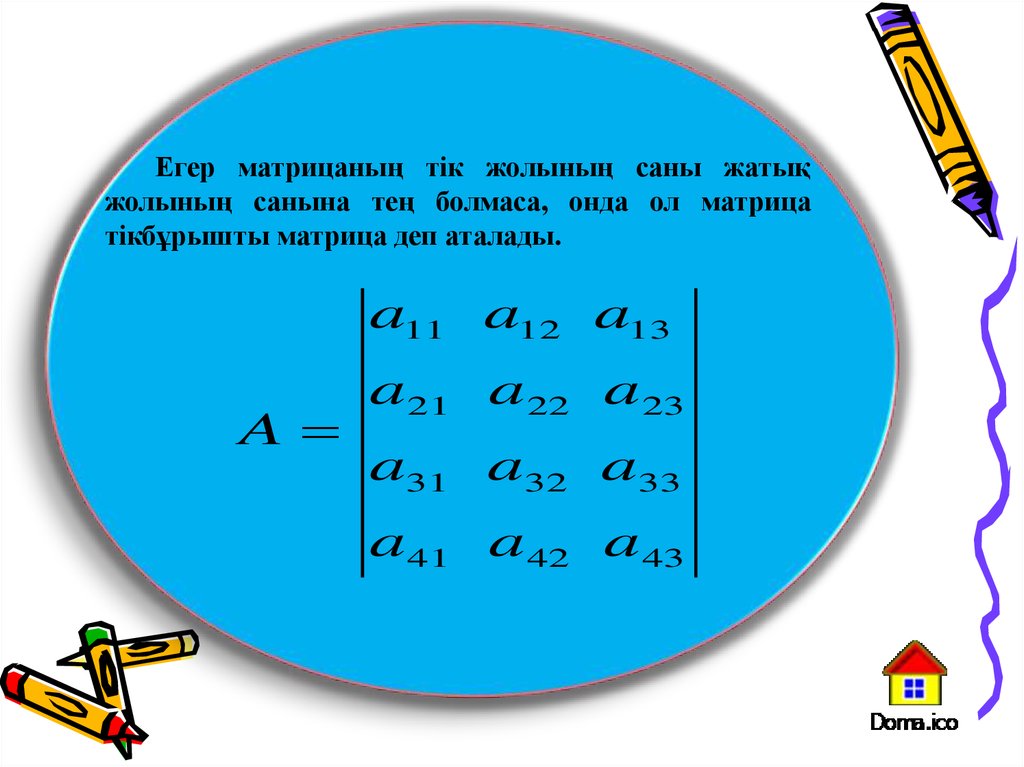
Егер матрицаның тік жолының саны жатықжолының санына тең болмаса, онда ол матрица
тікбұрышты матрица деп аталады.
a11 a12 a13
A
a 21 a 22 a 23
a31 a32 a33
a 41 a 42 a 43
6.
Егер матрицаның жатық жолының саны тікжолының санына тең болса, онда матрица
квадратты матрица деп аталады.
a11 a12 a1n
A a 21 a 22 a 2 n
a31 a32 a33
7.
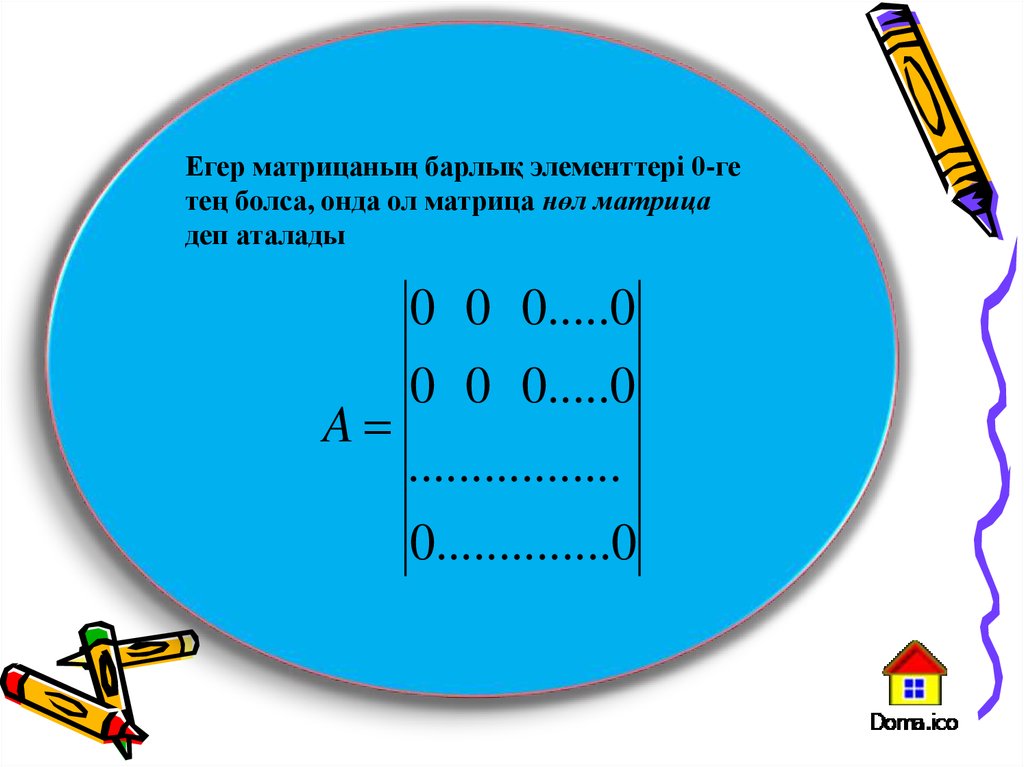
Егер матрицаның барлық элементтері 0-гетең болса, онда ол матрица нөл матрица
деп аталады
0 0 0.....0
A
0 0 0.....0
.................
0..............0
8.
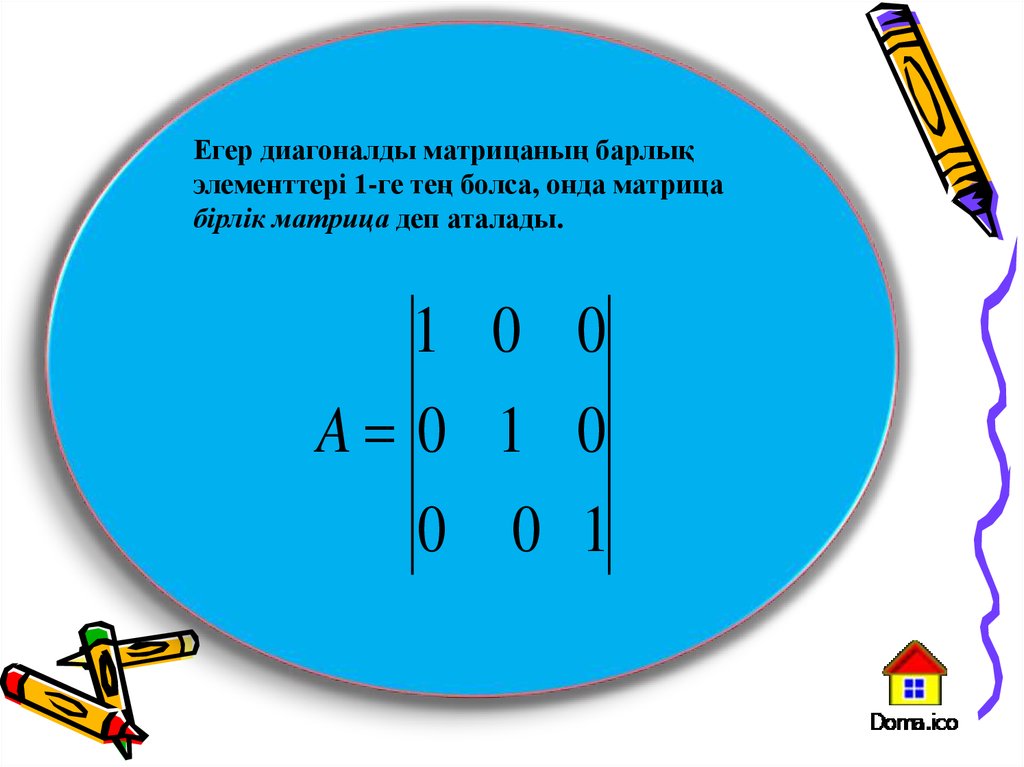
Егер диагоналды матрицаның барлықэлементтері 1-ге тең болса, онда матрица
бірлік матрица деп аталады.
1 0 0
A 0 1 0
0 0 1
9.
Егер матрицаның негізгі диагоналыныңэлементтерінен өзге элементтері нөлге тең
болса, онда матрица диагоналды матрица
деп аталады.
a11 0 0
A 0
a 22 0
0
0 a33
10.
Егер негізгі диагоналдан төмен немесежоғары орналасқан элементтері 0-ге тең
болса, онда квадратты матрица
үшбұрышты матрица деп аталады.
a11 a12 a1n
A 0
0
a 22 a 2 n
0
a33
a11 0
0
A a 21 a 22 0
a31 a32 a33
11.
Егер матрица бір жатық (тік) жолдан анықталса,онда матрица жатық (тік) жолды матрица
деп аталады.
a11
A a 21
a31
B a11 a12 .... a1n
12.
Алгебралыққосындысы
Қасиеті
Матрицаларға
амалдар қолдану
Матрицаны
матрицаға
көбейту
Қасиеті
Санға көбейту
Қасиеті
13.
Бірдей ретті A aij , B bij матрицаларының алгебралыққосындысы деп-сол ретті
C cij
матрицасын айтамыз.
C A B
және оның кез-келген элементтері мына формуладан анықталады:
C aij bij
i 1, m,
j 1, n
a11 a12 ...a1n b11 b12 ...b1n a11 b11 a12 b12 .....a1n b1n
C A B .................. .................. .............................................
a
a
a
b
b
b
a
b
a
b
a
b
m1 m 2..... mn m1 m 2..... mn m1 m1 m 2 m 2...... mn mn
14.
Ауыстырымдылық қасиет: А+В=В+АТерімділік қасиет:
А+0=А
А+(-А)=0
(А+В)+С=А+(В+С)
15.
Кез-келген А матрицанысанына көбейту деп-
C A íåìåñå C A және оның кез-келген элементтері
мына формуламен анықталады:
Ñij aij ,
i 1, m, j 1, n
16.
Сандар көбейткіштеріне терімділік қасиет:A A
Матрицалардың қосындыларына терімділік қасиет:
( A B) A B
Сандардың қосындысына үлестірімділік қасиет:
( ) A A
17.
Берілген m n ретті А матрицасының n k реттіВ матрицасына көбейтіндісі деп- m k ретті С матрицаны айтамыз.
C A B
n
C ij aik bkj .
i 1
i 1, m, j 1, n
18.
Матрицаны көбейткіштеріне терімділік қасиет:A BC AB C
Матрицалардың қосындыларына үлестірімділік қасиет:
( A B) C AC BC












 mathematics
mathematics








