Similar presentations:
Регулярные линии передачи электромагнитной энергии. Тема 4
1. Тема 4. РЕГУЛЯРНЫЕ ЛИНИИ ПЕРЕДАЧИ ЭЛЕКТРОМАГНИТНОЙ ЭНЕРГИИ Лекция № 13. Длинные линии.
1. Длинные линии: их классификация ипараметры.
2. Методика нахождения параметров линии с
помощью измерительной линии.
3. Круговая диаграммы полных сопротивлений.
Электромагнитные поля и волны. Лекция 13.
1
2. 1 Длинные линии: их классификация и параметры
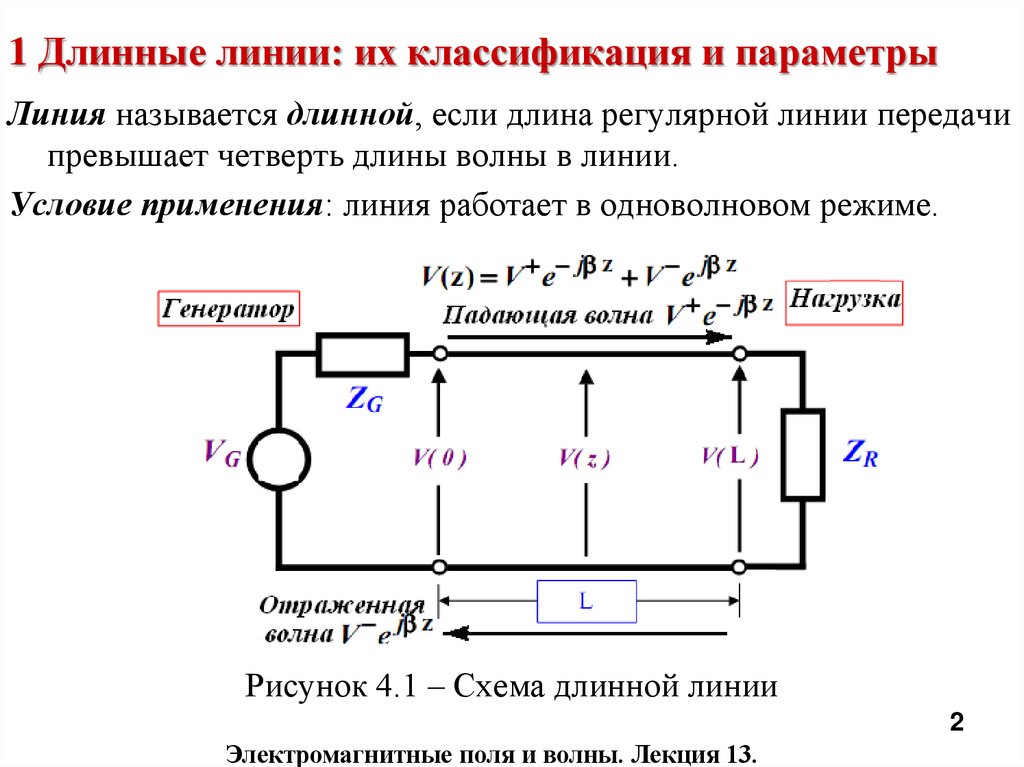
Линия называется длинной, если длина регулярной линии передачипревышает четверть длины волны в линии.
Условие применения: линия работает в одноволновом режиме.
Рисунок 4.1 – Схема длинной линии
2
Электромагнитные поля и волны. Лекция 13.
3.
Особенности применения аппарата длинных линийПроцессы, протекающие в линии, определяются амплитуднофазовыми соотношениями между падающей и отраженной
волнами. Отказ от электродинамики. Применение упрощенного
математического аппарата – схем замещения
(эквивалентных длинных линий). Для описания процессов в
линии применяются величины напряжения и тока.
Физические свойства длинной линии определяются значениями
четырех распределенных вдоль ее длины параметров:
индуктивности L, емкости C, продольного активного
сопротивления R и поперечной активной проводимости G.
В диапазоне СВЧ исключается погонное сопротивление и погонная
проводимость (потери энергии малы) – линии без потерь.
Линия называется однородной, если параметры распределены
вдоль линии равномерно (т.е. не зависят от z). В противном
случае - неоднородная линия.
Электромагнитные поля и волны. Лекция 13.
3
4.
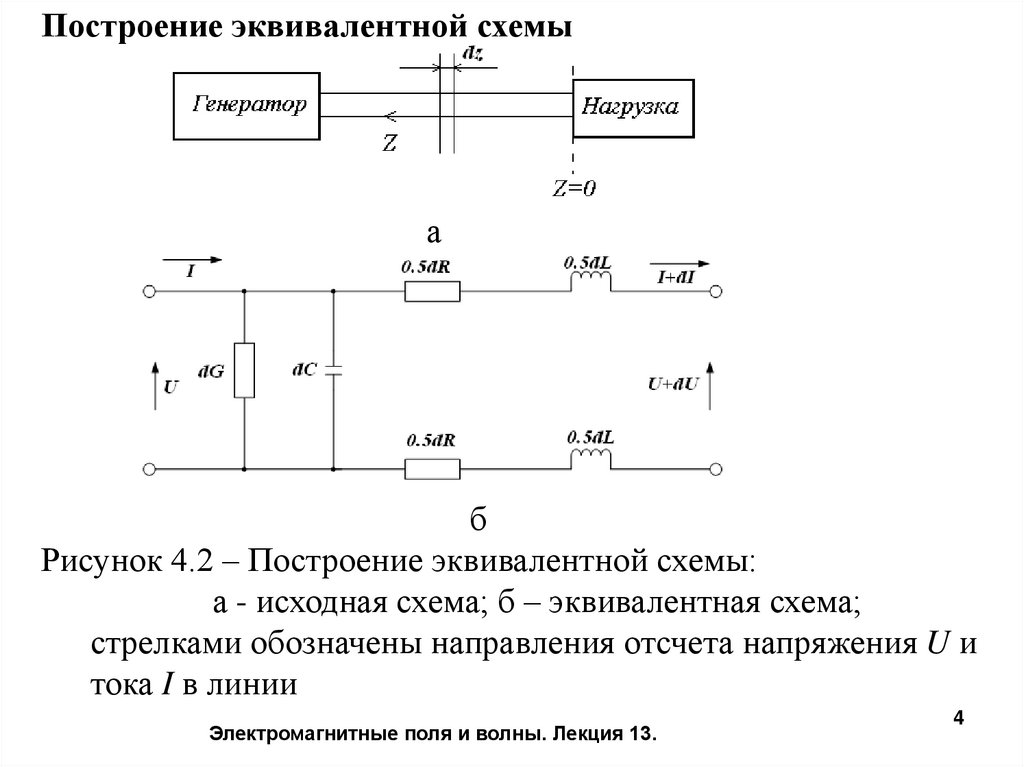
Построение эквивалентной схемыа
б
Рисунок 4.2 – Построение эквивалентной схемы:
а - исходная схема; б – эквивалентная схема;
стрелками обозначены направления отсчета напряжения U и
тока I в линии
Электромагнитные поля и волны. Лекция 13.
4
5.
Телеграфные уравненияПриращения напряжения и тока на участке dz:
dU I dR i dL ,
dI U dG i dC .
dU
IZ ,
Телеграфные уравнения:
dz
Волновые уравнения:
где ZY
.
(4.2)
2
d 2U
d
I
2
2
U
0
I 0 ,
,
2
2
dz
dz
(4.3)
R i L G i C i
Решение уравнения (4.3):
U AU exp( z) BU exp( z) ,
падающая
волна
dI
UY
dz
(4.1)
- коэффициент
распространения в длинной лини.
I AI exp( z) BI exp( z) . (4.4)
отраженная
волна
Электромагнитные поля и волны. Лекция 13.
5
6.
Определение параметров длинной линииКомплексный коэффициент отражения Г определяет степень
согласования линии передачи с нагрузкой:
BU
(4.6)
AU
Два способа определения: в месте нагрузки (Г(0)) и в произвольной
точки линии (Г(z)):
( z ) (0) exp( 2i z )
(4.7)
Нормированное сопротивление нагрузки: Z н / W Z~н 1 (4.8)
1
~
1 Zн
Взаимосвязь между сопротивлением нагрузки и КО: W
~
1 Zн
Волновое сопротивление линии W не изменяется и считается
известным.
Электромагнитные поля и волны. Лекция 13.
6
7.
Коэффициент бегущей волны КБВ определяет степеньсогласования линии с нагрузкой:
AU BU 1
КБВ
AU BU 1
(4.9)
Коэффициент стоячей волны по напряжению КСВН определяет
степень рассогласования линии с нагрузкой:
КСВН
AU BU 1 U max
AU BU 1 U min
(4.10)
Коэффициент полезного действия:
1
2
(4.11)
Входное сопротивление линии:
1 (0) exp( 2 z )
Z вх ( z ) W
1 (0) exp( 2 z )
(4.12)
7
Электромагнитные поля и волны. Лекция 13.
8.
Таблица 4.1 – Режимы работы линииРежимы работы
линии
Режим бегущей
волны
Параметры
линии
0
КБВ=КСВН=1
Характеристика работы
Только падающая волна,
распространяющаяся от генератора к
нагрузке. Мощность полностью выделяется
в нагрузке.
Режим смешанных
волн
0 1
0 КБВ 1
1 КCВН
Часть мощности падающей волны теряется
в нагрузке, а остальная часть в виде
отраженной волны возвращается обратно в
генератор.
Режим стоячей
волны
1
Амплитуда отраженной волны равна
амплитуде падающей. Энергия падающей
волны полностью отражается от нагрузки и
возвращается в обратно в генератор
КБВ=0,
КСВН
Электромагнитные поля и волны. Лекция 13.
8
9. 2 Методика нахождения параметров линии с помощью измерительной линии
Рисунок 4.2 – Измерительная линия на основе отрезкакоаксиального кабеля
Рисунок 4.3 – Измерительная линия на основе отрезка волновода
Электромагнитные поля и волны. Лекция 13.
9
10.
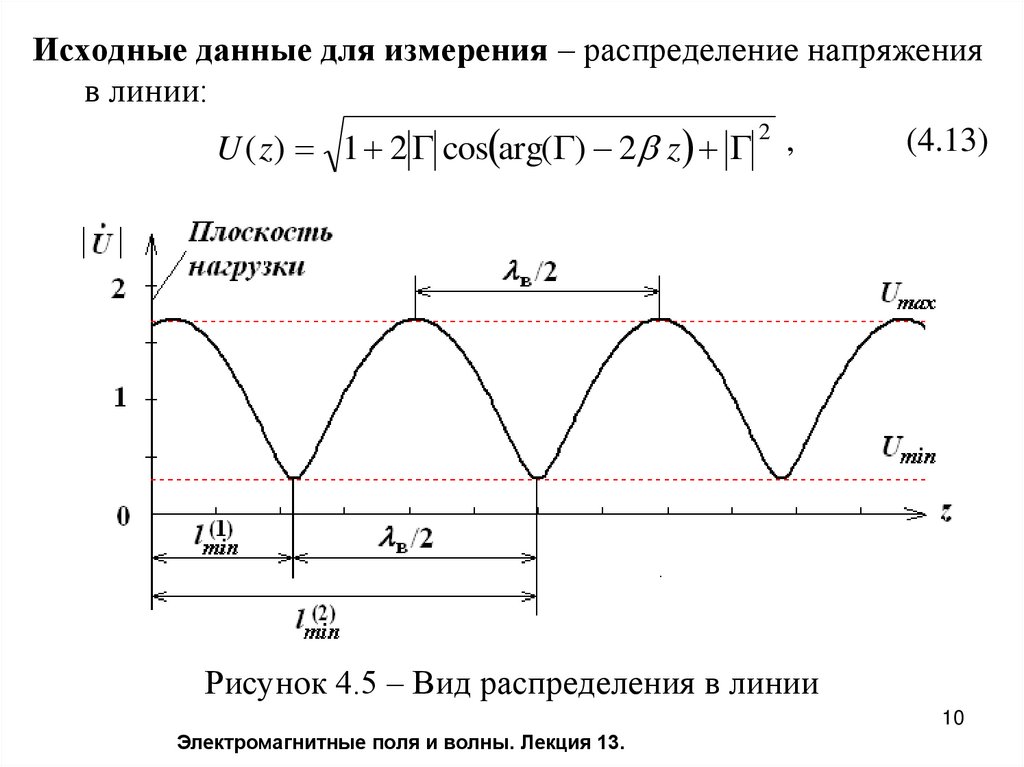
Исходные данные для измерения – распределение напряженияв линии:
2 ,
(4.13)
U ( z ) 1 2 cos arg( ) 2 z
Рисунок 4.5 – Вид распределения в линии
10
Электромагнитные поля и волны. Лекция 13.
11.
Методика измерения:1. По измеренным значениям минимального и максимального
значений напряжения вычисляется КСВН:
(4.14)
U max
КСВН
2. Определение модуля КО:
U min
3. Вычисление длины волны в линии
2)
1)
в 2 (min
(min
КСВН - 1
КСВН 1
4. Определение фазы коэффициента отражения
2 min ,
2
где .
(4.15)
(4.16)
(4.17)
в
5. Расчет комплексного коэффициента отражения:
exp(i )
Электромагнитные поля и волны. Лекция 13.
(4.18)
11
12.
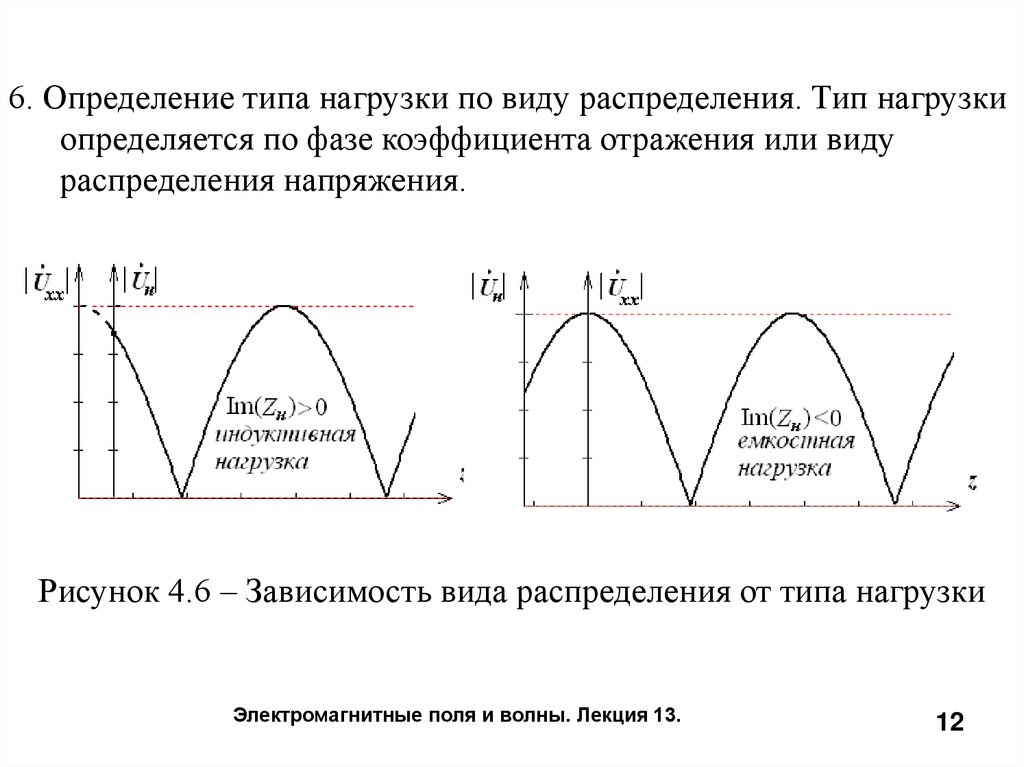
6. Определение типа нагрузки по виду распределения. Тип нагрузкиопределяется по фазе коэффициента отражения или виду
распределения напряжения.
Рисунок 4.6 – Зависимость вида распределения от типа нагрузки
Электромагнитные поля и волны. Лекция 13.
12
13.
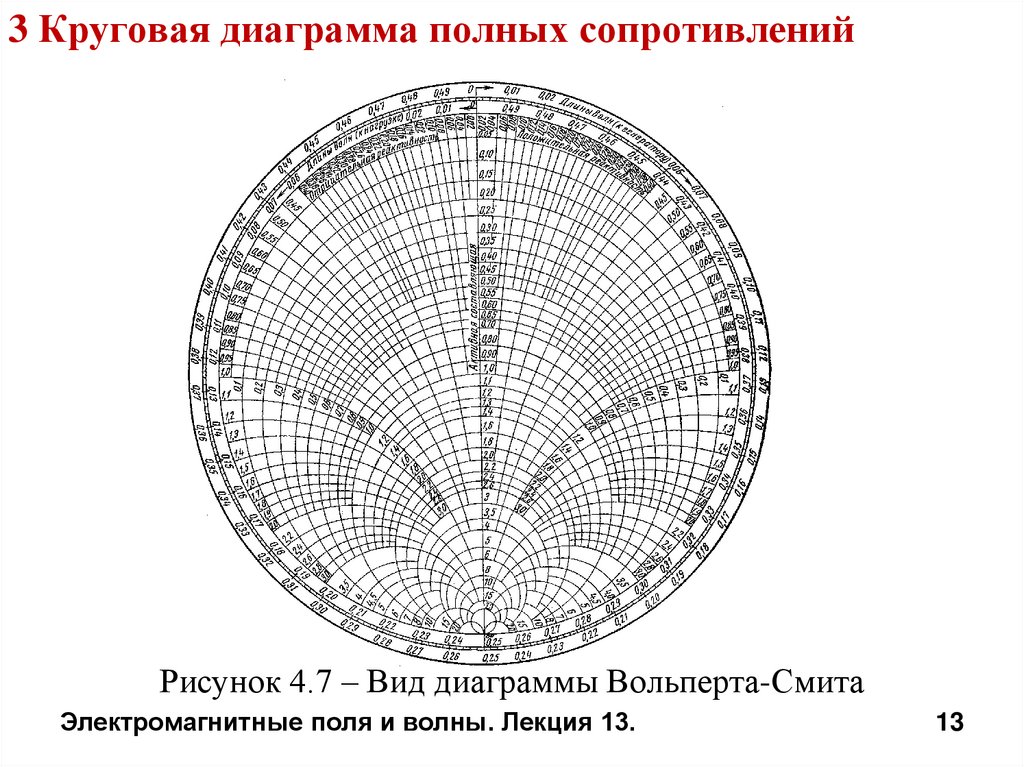
3 Круговая диаграмма полных сопротивленийРисунок 4.7 – Вид диаграммы Вольперта-Смита
Электромагнитные поля и волны. Лекция 13.
13
14.
Пример применения круговой диаграммы полныхсопротивлений для решения задачи нахождения параметров
длинной линии.
Постановка задачи: По заданному комплексному сопротивлению
нагрузки Z 25 i100 Ом и характеристическому
сопротивлению линии 50 Ом определить коэффициент
отражения в линии.
Решение задачи будем проводить следующим образом.
1. Определение нормированного сопротивления нагрузки:
Z
(4.19)
z
W
(25 i100) / 50 0.5 i 2.0
2. На диаграмме Вольперта ищем окружность, имеющую радиус
r 0.5
3. Поиск дуги, соответствующей значению реактанса x 2.0
4. Вычисление комплексного значения коэффициента отражения Г.
Электромагнитные поля и волны. Лекция 13.
14
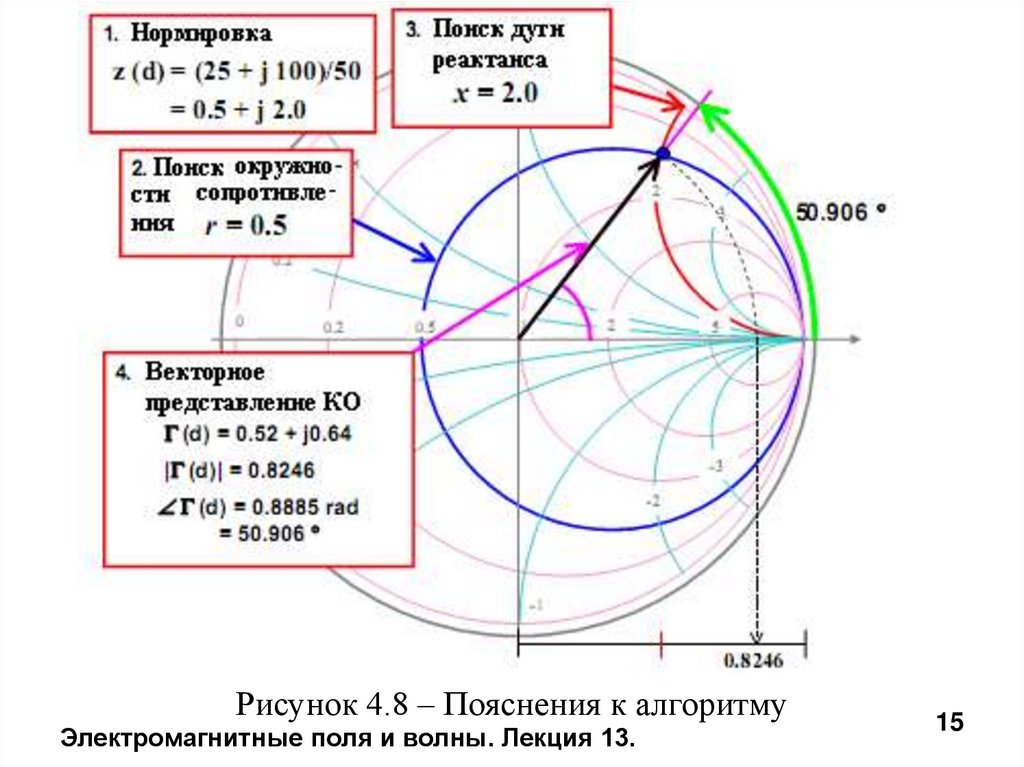
15.
Рисунок 4.8 – Пояснения к алгоритмуЭлектромагнитные поля и волны. Лекция 13.
15









 physics
physics








