Similar presentations:
Комплексные числа
1. Комплексные числа
Выполнили :студентки 1 курса
специальности
СЗС-12 Куликова
Анастасия и
Мосалева Анна.
2. Определение
Комплексными числами называют числавида a + bi , где a и b – действительные
числа, число i .определяемое равенством
i2 = -1, называется мнимой единицей.
3. a + bi
a – действительная часть комплексногочисла
b – мнимая часть комплексного числа
4. Определение
Числа вида Z = bi называют чисто мнимымчислом.
Модулем комплексного числа Z = a + bi
называется число, которое определяется по
формуле.
Например:
Z = - 4 – 5i
5.
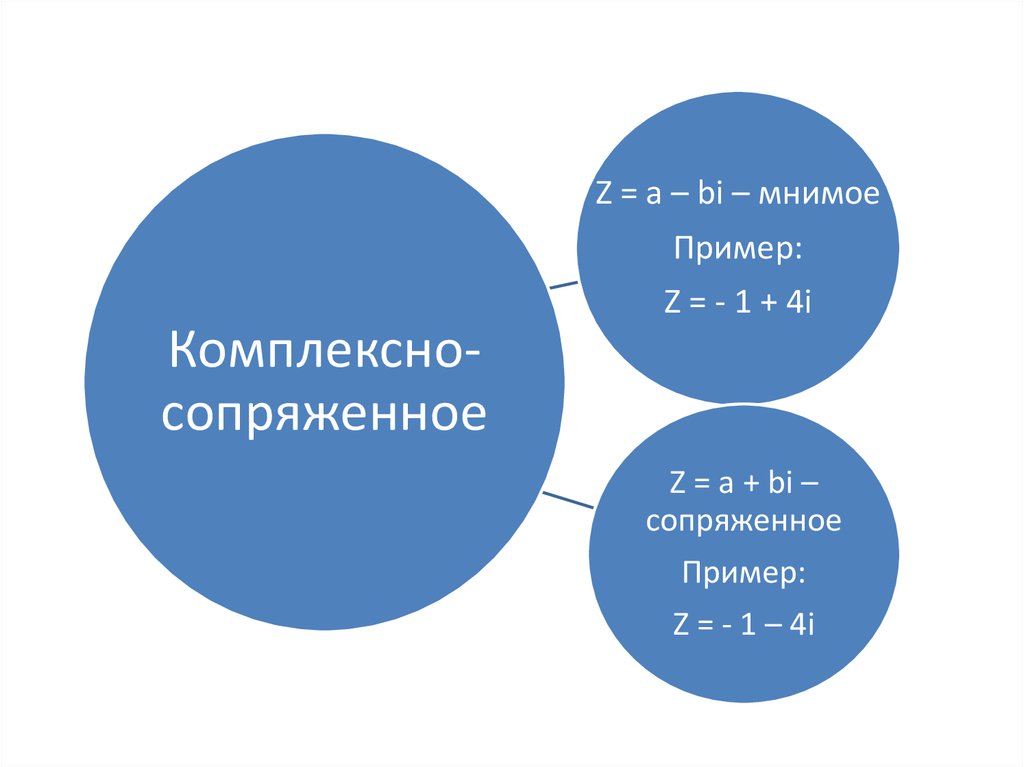
Z = a – bi – мнимоеПример:
Z = - 1 + 4i
Комплексносопряженное
Z = a + bi –
сопряженное
Пример:
Z = - 1 – 4i
6. Свойство
Два комплексных числаZ 1 = a1 + b 1 i
Z 2 = a2 + b 2 i ;
Называются равными, если a1 = a2 ;
b1 = b2
7. Действия над комплексными числами
• Сравнение :• a+bi=c+di означает, что a=c и b=d(два комплексных
числа равны между собой тогда и только тогда,
когда равны их действительные и мнимые части).
• Сложение:
• (a+bi)+ (c+di)=(a+c)+(b+d)i.
• Вычитание:
• (a+bi)-(c+di)=(a-c)+(b-d)i.
• Умножение:
• (a+bi)(c+di)=ac+bci+adi+bdi2=(ac-bd)+ (bc+ad)i.
• Деление:
• a+bi =(a+bi)(c-di) = ac+bd +(bc-ad)i
• c+di (c+di)(c-di) c2+b2 (c2+d2)i






 mathematics
mathematics








