Визначення математичної моделі теплообменника - калорифер

1.

ВИЗНАЧЕННЯ
МАТЕМАТИЧНОЇ МОДЕЛІ
ТЕПЛООБМЕННИКА - КАЛОРИФЕР

2.

ІДЕНТИФІКАЦІЯ – процес визначення характеристик
об’єкту керування за даними
експериментальних досліджень.
СПОСОБИ ОТРИМАННЯ МАТЕМАТИЧНИХ МОДЕЛЕЙ ОБ’ЄКТУ КЕРУВАННЯ:
– аналітичний;
– експериментальний;
– експериментально-аналітичний.
ВИДИ ІДЕНТИФІКАЦІЇ:
– структурна;
– параметрична.

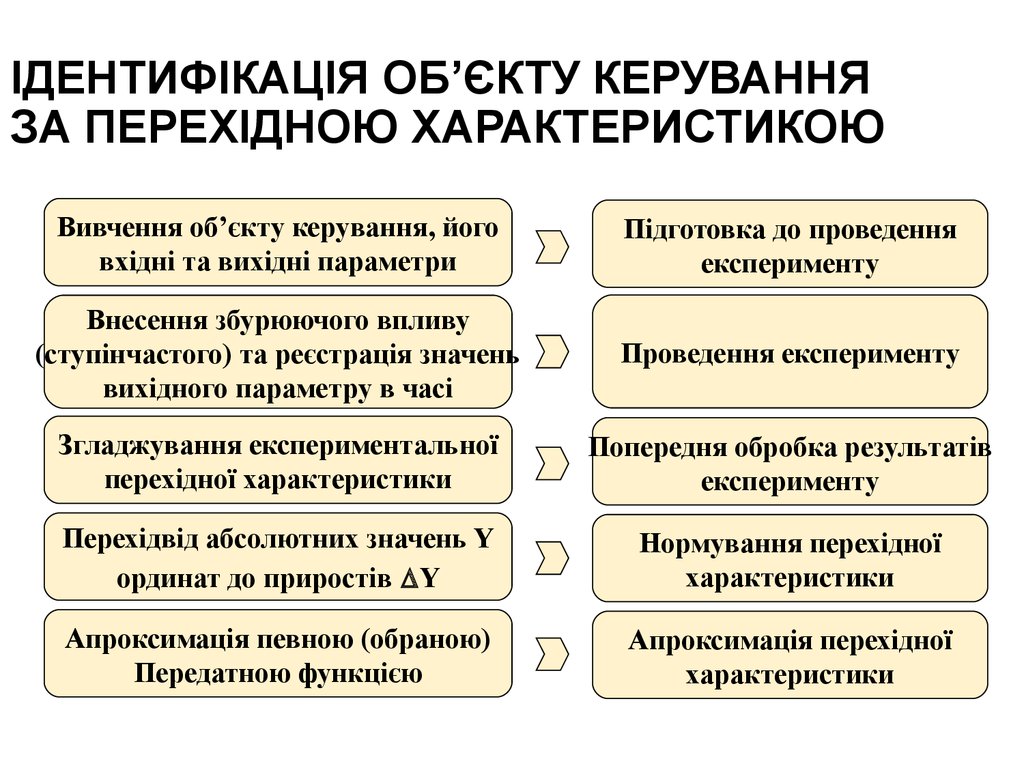
3. ІДЕНТИФІКАЦІЯ ОБ’ЄКТУ КЕРУВАННЯ ЗА ПЕРЕХІДНОЮ ХАРАКТЕРИСТИКОЮ

Вивчення об’єкту керування, його
вхідні та вихідні параметри
Підготовка до проведення
експерименту
Внесення збурюючого впливу
(ступінчастого) та реєстрація значень
вихідного параметру в часі
Проведення експерименту
Згладжування експериментальної
перехідної характеристики
Попередня обробка результатів
експерименту
Перехідвід абсолютних значень Y
ординат до приростів Y
Нормування перехідної
характеристики
Апроксимація певною (обраною)
Передатною функцією
Апроксимація перехідної
характеристики

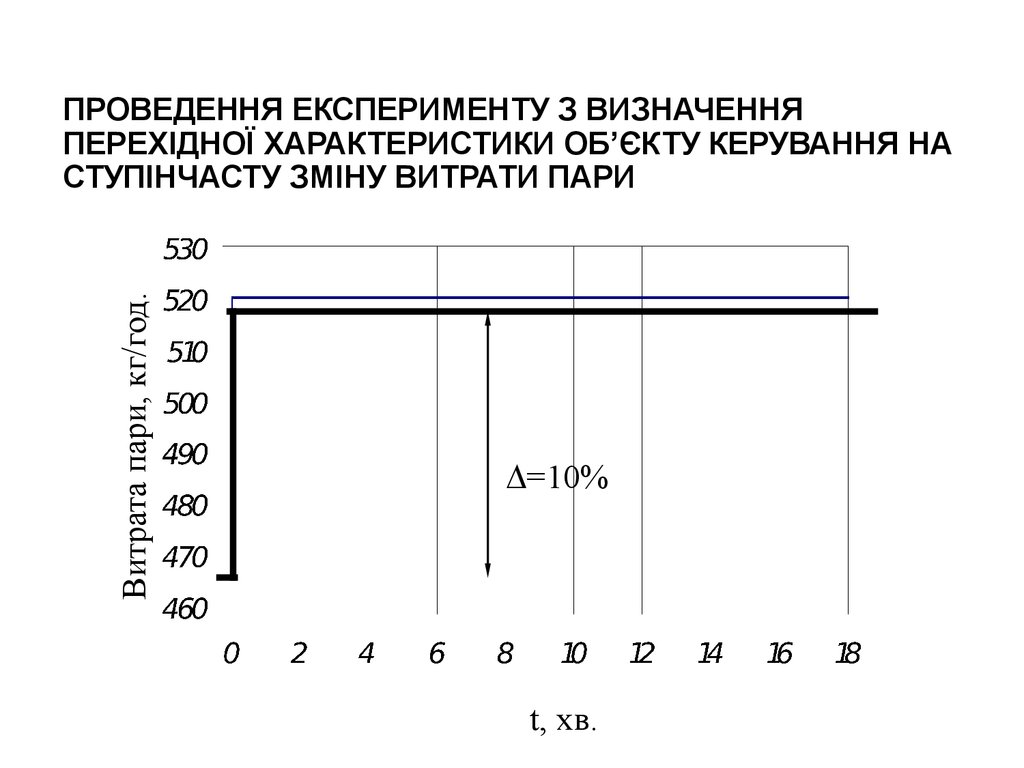
4. ПРОВЕДЕННЯ ЕКСПЕРИМЕНТУ З ВИЗНАЧЕННЯ ПЕРЕХІДНОЇ ХАРАКТЕРИСТИКИ ОБ’ЄКТУ КЕРУВАННЯ НА СТУПІНЧАСТУ ЗМІНУ ВИТРАТИ ПАРИ

Витрата пари, кг/год.
ПРОВЕДЕННЯ ЕКСПЕРИМЕНТУ З ВИЗНАЧЕННЯ
ПЕРЕХІДНОЇ ХАРАКТЕРИСТИКИ ОБ’ЄКТУ КЕРУВАННЯ НА
СТУПІНЧАСТУ ЗМІНУ ВИТРАТИ ПАРИ
=10%
t, хв.

5. Експериментальна крива

t, C
Експериментальна крива
t, хв.

6. ПОПЕРЕДНЯ ОБРОБКА РЕЗУЛЬТАТІВ ЕКСПЕРИМЕНТУ

Для визначення корисного сигналу з експериментальної
перехідної харак-теристики, використовуємо метод послідовного
усереднення. Метод полягає в тому, що на деякому інтервалі часу L t
(L-ціле число) виконують послідовне усереднення ординат z i
(i=0,1,2,3…,n) за на ступним алгоритмом:
L
*
*i+L/2
i+L/2
h
h
1 L
= 1 å zi+β
= L+1 β=0
zi+β
å
L+1 β=0
де h* - ординати усередненої характеристики;
zi+ - ордината експериментально отриманої точки;
і – порядковий номер точки.
Точність усереднення залежить від числа L, при малому значенні
L якість згладжування буде низько, а збільшення L може призвести до
викривлення суттєвих особливостей часової характеристики.
Якість згладжування оцінюється експериментально.

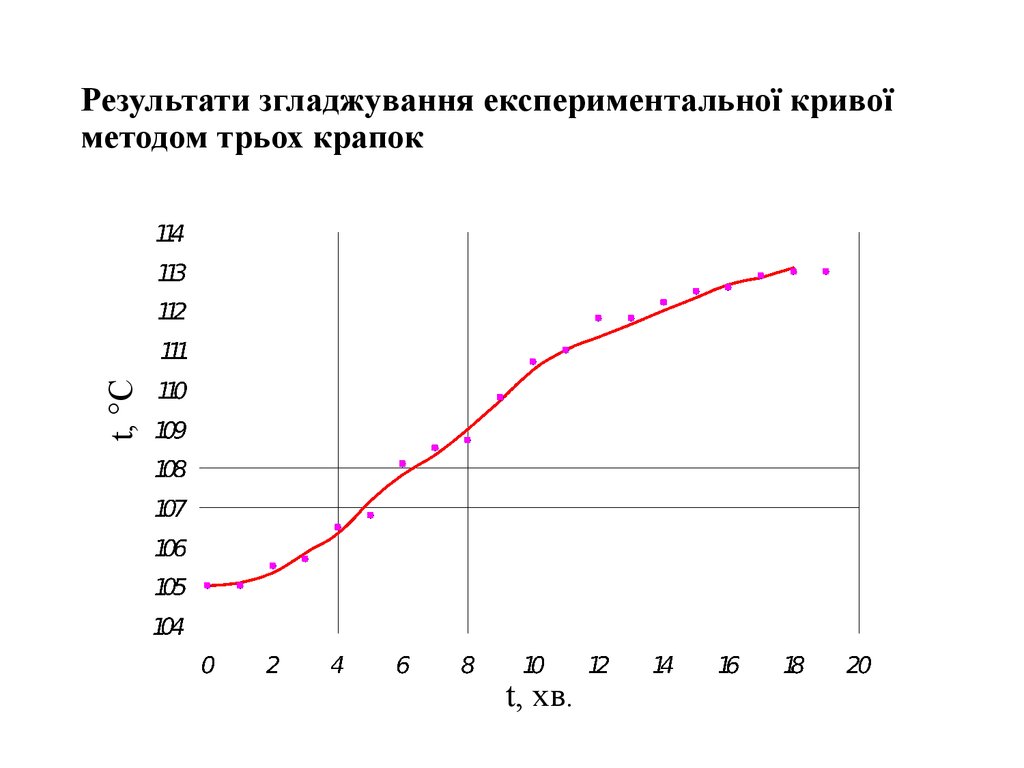
7. Результати згладжування експериментальної кривої методом трьох крапок

t, C
Результати згладжування експериментальної кривої
методом трьох крапок
t, хв.

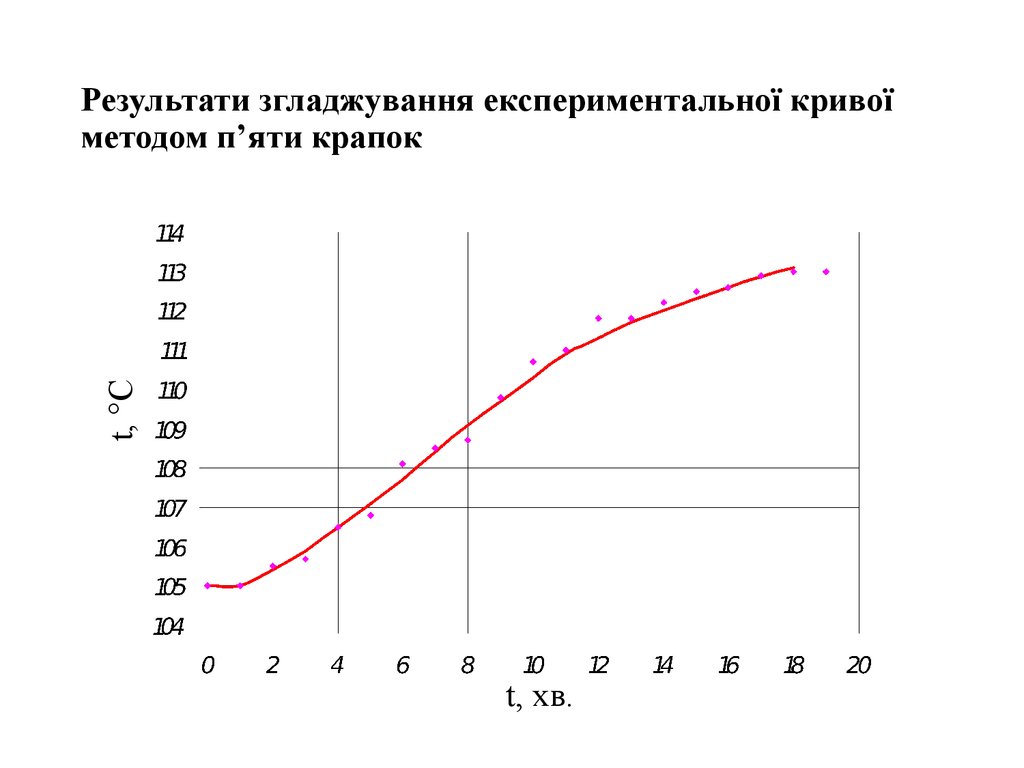
8. Результати згладжування експериментальної кривої методом п’яти крапок

t, C
Результати згладжування експериментальної кривої
методом п’яти крапок
t, хв.

9. АПРОКСИМАЦІЯ ОДЕРЖАНОЇ ПЕРЕХІДНОЇ ХАРАКТЕРИСТИКИ АПЕРІОДИЧНОЮ ЛАНКОЮ ДРУГОГО ПОРЯДКУ ТА ЛАНКОЮ ЗАПІЗНЮВАННЯ

•Метод Симою є універсальним методом
апроксимації,
який
дозволяє
отримати
апроксимуючі залежності будь якого порядку. Цей
метод маючи високу точність апроксимації, в
порівнянні з іншими методами відрізняється тим,
що він легко алгоритмується та легко обробляється
на ЕОМ.
•Апроксимуючою залежністю є дрібнораціональна передатна функція виду:
K × e-pτ
W(p)=
a n p n +a n-1p n-1 +...+a1p+1
де
T(¥)-T(0)
F(0)
K=
×
T(0)
F(¥)-F(0)

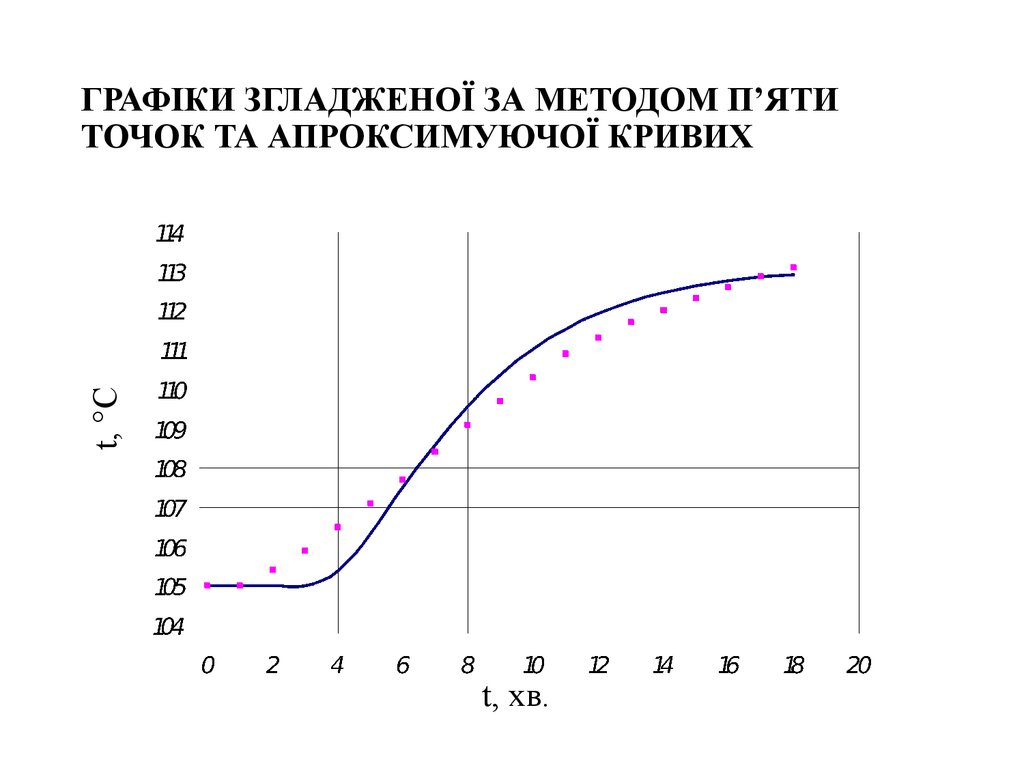
10. ГРАФІКИ ЗГЛАДЖЕНОЇ ЗА МЕТОДОМ П’ЯТИ ТОЧОК ТА АПРОКСИМУЮЧОЇ КРИВИХ

t, C
ГРАФІКИ ЗГЛАДЖЕНОЇ ЗА МЕТОДОМ П’ЯТИ
ТОЧОК ТА АПРОКСИМУЮЧОЇ КРИВИХ
t, хв.

11.

РЕЗУЛЬТАТИ АПРОКСИМАЦІЇ:
Передатна функція 2-го порядку
Точність апроксимації 89,3%
Коефіцієнт передатної функції:
Т1= 2,48 хв;Т2=2,98 хв.
Коефіцієнт передачі:
К(б/р)=0,75; К(р)=0,116 (оС/(кг/год));
Час запізнення =3хв.
Передатна функція у безрозмірному виді:
-3p
0.75×e
W(p)=
(2.48р+1)×(2.985р+1)

12. АПРОКСИМАЦІЯ ОДЕРЖАНОЇ ПЕРЕХІДНОЇ ХАРАКТЕРИСТИКИ МЕТОДОМ СИМОЮ

Метод
Симою
є
універсальним
методом
апроксимації, який дозволяє отримати апроксимуючі
залежності будь якого порядку. Цей метод маючи
високу точність апроксимації, в порівнянні з іншими
методами відрізняється тим, що він легко
алгоритмується та легко обробляється на ЕОМ.
Апроксимуючою
залежністю
є
дрібнораціональна передатна функція виду:
K × e-pτ
W(p)=
a n p n +a n-1p n-1 +...+a1p+1
де
T(¥)-T(0)
F(0)
K=
×
T(0)
F(¥)-F(0)

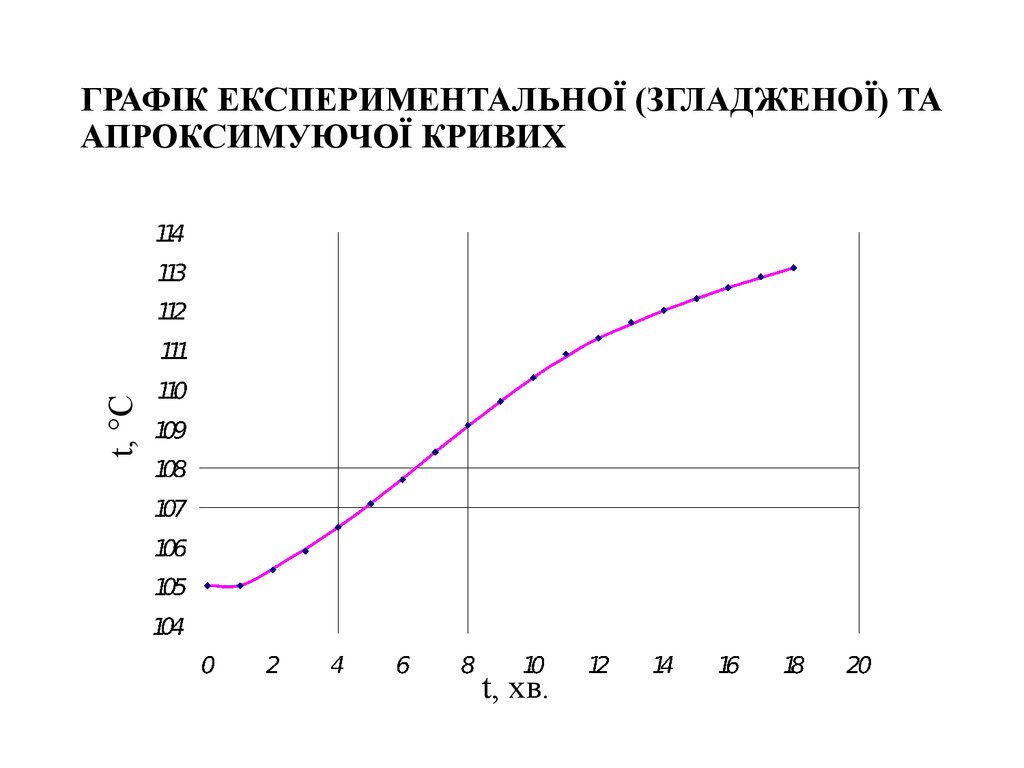
13. ГРАФІК ЕКСПЕРИМЕНТАЛЬНОЇ (ЗГЛАДЖЕНОЇ) ТА АПРОКСИМУЮЧОЇ КРИВИХ

t, C
ГРАФІК ЕКСПЕРИМЕНТАЛЬНОЇ (ЗГЛАДЖЕНОЇ) ТА
АПРОКСИМУЮЧОЇ КРИВИХ
t, хв.

14.

РЕЗУЛЬТАТИ АПРОКСИМАЦІЇ:
Передатна функція 2-го порядку
Точність апроксимації 99,6%
Коефіцієнт передатної функції:
а1=7,42 хв; а2=17,84 хв2.
Коефіцієнт передачі:
К(б/р)=0,75; К(р)=0,116 (оС/(кг/год));
Час запізнення =1хв.
Передатна функція у безрозмірному виді:
0.75 × e-1p
W(p)=
17.84p 2 +7.42p+1