Система дослідження методу згладжування ковзними відрізками

1.

ОДЕСЬКИЙ НАЦІОНАЛЬНИЙ МОРСЬКИЙ УНІВЕРСИТЕТ
Кафедра технічної кібернетики й інформаційних технологій
ім. професора Р.В. Меркта
Кваліфікаційна робота бакалавра
«Система дослідження методу
згладжування ковзними відрізками»
Здобувач вищої освіти
4 курса ННІІТтаІП:
Ігор БОРТНЯ
Керівник:
к.т.н., професор
Віктор ЧЕЛАБЧІ
Одеса 2024

2. Актуальність роботи

Натурний експеримент і фізичне моделювання вимагає
значних матеріальних і фінансових витрат, а часто практично
неможливі. Обчислювальний експеримент на основі
математичного моделювання дозволяє провести дослідження
швидше і дешевше.
Експериментальні дані містять похибки, пов'язані з технікою
проведення вимірювань, а також вплив сторонніх факторів,
які
неможливо
врахувати
у
методиці
проведення
експерименту.
Проведення тестування, що спирається на модельні дані, має
пряму економічну доцільність.
2

3. Цілі і завдання

Провести аналітичний огляд методів та алгоритмів,
які використовуються у згладжування даних з
шумом;
Реалізувати алгоритм згладжування
експериментальних даних, які представлені у
вигляді часових рядів;
Вибрати вид апроксимуючої залежності та
реалізувати алгоритм апроксимації;
Реалізувати методи визначення статистичних
характеристик вибірки випадкових величин.
3

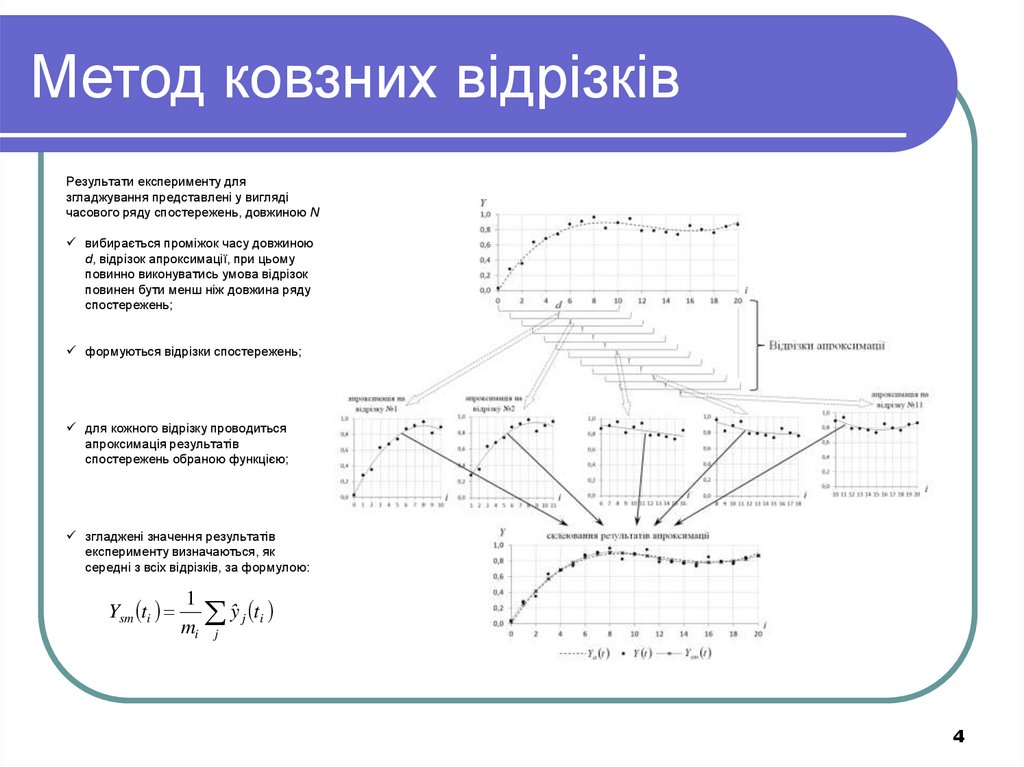
4. Метод ковзних відрізків

Результати експерименту для
згладжування представлені у вигляді
часового ряду спостережень, довжиною N
вибирається проміжок часу довжиною
d, відрізок апроксимації, при цьому
повинно виконуватись умова відрізок
повинен бути менш ніж довжина ряду
спостережень;
формуються відрізки спостережень;
для кожного відрізку проводиться
апроксимація результатів
спостережень обраною функцією;
згладжені значення результатів
експерименту визначаються, як
середні з всіх відрізків, за формулою:
Ysm ti
1
ŷ j ti
mi j
4

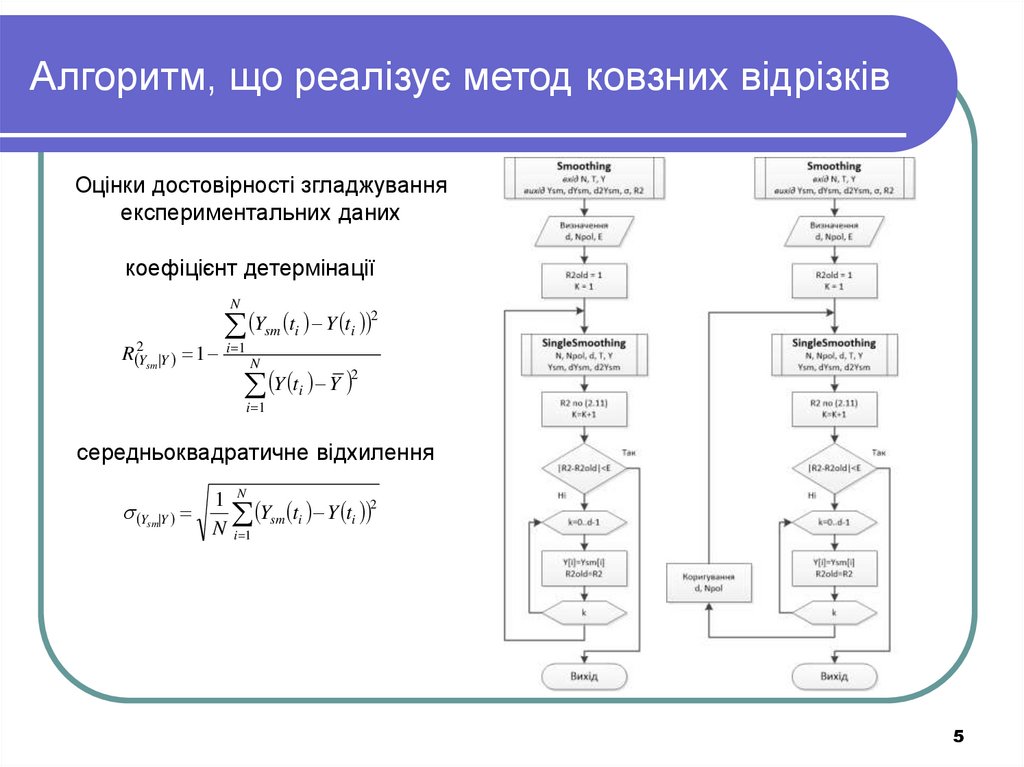
5. Алгоритм, що реалізує метод ковзних відрізків

Оцінки достовірності згладжування
експериментальних даних
коефіцієнт детермінації
N
Ysm ti Y ti 2
R 2Ysm |Y 1 i 1 N
Y ti Y
2
i 1
середньоквадратичне відхилення
1 N
Ysm ti Y ti 2
Ysm|Y
N i 1
5

6. Апроксимація поліномом

Система лінійних алгебраїчних рівнянь
для знаходження коефіцієнтів
апроксимуючого полінома
d
d
tk
k 1
d
d
2
tk tk
k 1
k 1
d 2 d 3
tk tk
k 1
k 1
d
d
t kn t kn 1
k 1
k 1
d
Yk
k 1
k 1
k 1
d
d
d
3
n 1 b0
t
t
t
Y
k
k b1 k k
k 1
k 1
k 1
d
d
d
b
2
4
n 2
2
t
t
t
k
k k Yk
k 1
k 1
k 1
bn
d
d
d
n 2
2n
n
t
t
t
Y
k
k
k k
k 1
k 1
k 1
d
t k2
d
t kn
Значення
апроксимуючої функції
та її похідних
n
Ya ti b p ti tip
p 0
dYa ti n
pbp ti tip 1 ,
dt
p 1
d 2Ya ti n
p p 1 b p ti tip 2 ,
2
dt
p 2
6

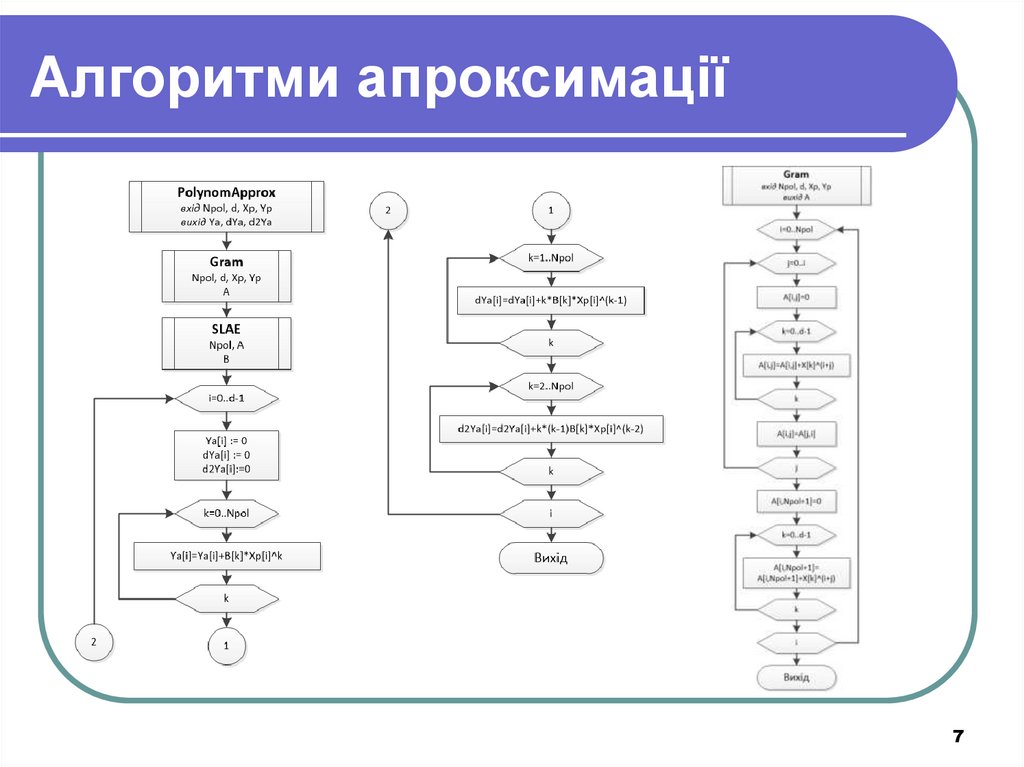
7. Алгоритми апроксимації

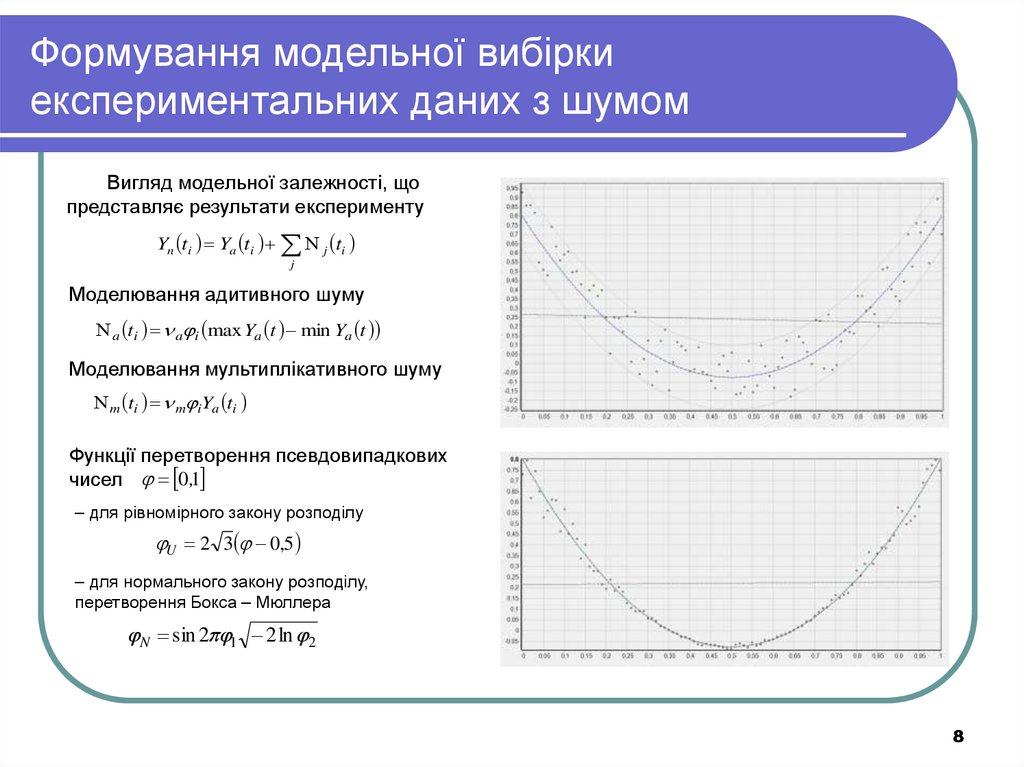
7

8. Формування модельної вибірки експериментальних даних з шумом

Вигляд модельної залежності, що
представляє результати експерименту
Yn ti Ya ti j ti
j
Моделювання адитивного шуму
a ti a i max Ya t min Ya t
Моделювання мультиплікативного шуму
m ti m iYa ti
Функції перетворення псевдовипадкових
чисел 0,1
– для рівномірного закону розподілу
U 2 3 0,5
– для нормального закону розподілу,
перетворення Бокса – Мюллера
N sin 2 1 2 ln 2
8

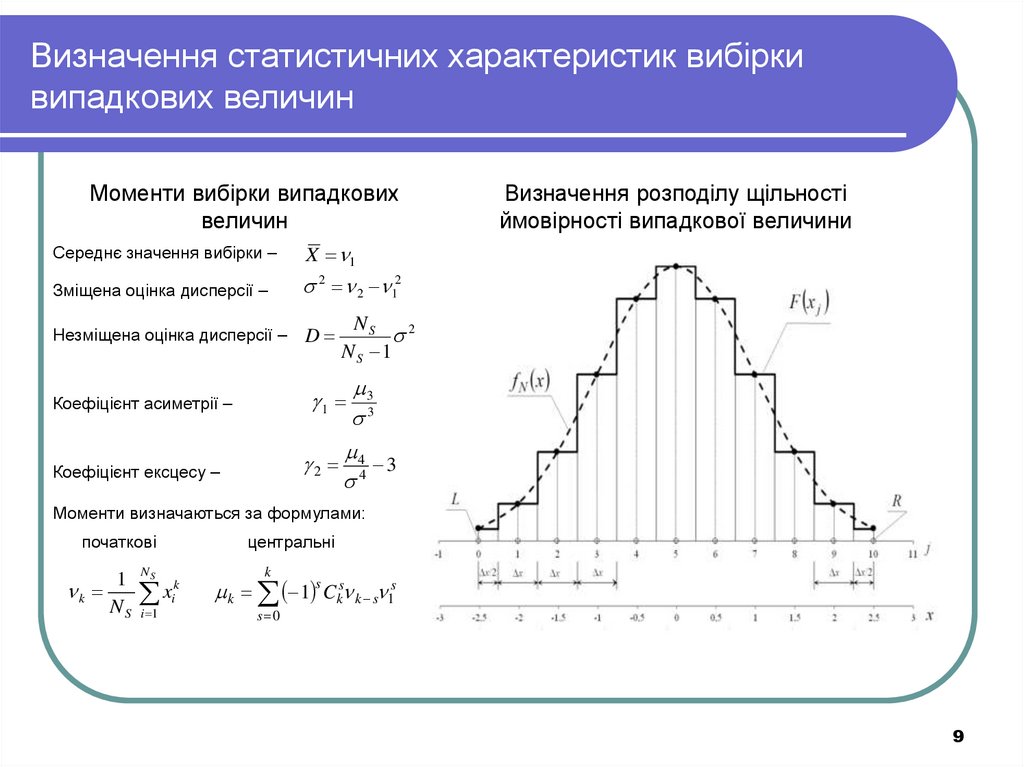
9. Визначення статистичних характеристик вибірки випадкових величин

Моменти вибірки випадкових
величин
Середнє значення вибірки –
X 1
Зміщена оцінка дисперсії –
2 2 12
Незміщена оцінка дисперсії –
D
Коефіцієнт асиметрії –
1
Коефіцієнт ексцесу –
2
Визначення розподілу щільності
ймовірності випадкової величини
NS
2
NS 1
3
3
4
3
4
Моменти визначаються за формулами:
початкові
k
1 NS k
xi
N S i 1
центральні
k
k 1 s Cks k s 1s
s 0
9

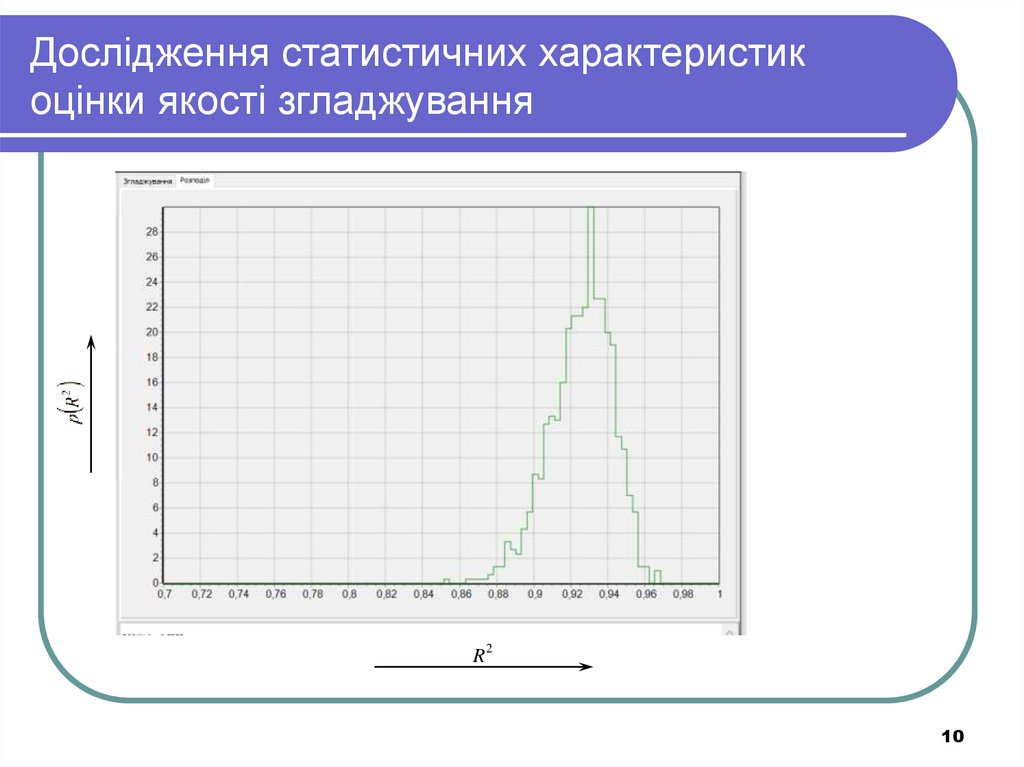
10. Дослідження статистичних характеристик оцінки якості згладжування

R2
10

11. Висновки

Проведений аналіз робот, які присвячені обробки
експериментальних даних;
Реалізований алгоритм методу згладжування
ковзними відрізками;
Реалізований алгоритм апроксимації набору даних
поліномом;
Розроблений метод та алгоритм розрахунку
статистичних характеристик вибірки випадкових
величин.
11