Методи представлення та опису

1.

Курс: Математичні методи обробки зображень
Лекція 9
Методи представлення та опису
Бучко Олена Андріївна [email protected]

2. Вступ

Перший крок сегментація, другий представлення та опис в зручній формі
для подальшої обробки.
Представлення: (1) об'єкт (область) можна представити її зовнішніми
характеристиками (тобто контуром) або (2) область можна представити
внутрішніми характеристиками (тобто сукупністю елементів зображення,
що складають цю область). Іноді доводиться використовувати обидва
способи подання одночасно.
Опис: описати область, виходячи з обраного способу подання.
Наприклад, область може бути представлена ​своїм контуром, а контур –
описаний за допомогою таких характеристик, як довжина кордону, площа,
кількість кутів.
Два класи методів представлення та опису форми:
контурні методи, (зовнішні), на основі інформації, витягнутої з контуру
об'єкта і його властивостей;
регіоні методи, (внутрішні), на основі інформації, витягнутої з області
форми (колір, текстура).
Два підходи :
структурний підхід, поділ контуру або області форми на сегменти або
частини – “примітиви”, за будь-яким критерієм;
2
глобальний підхід не ділить контур або область форми

3. Опис форми (shape description)

Процес знаходження інформації про об'єкт
Набір числових ознак, властивостей, дескрипторів
об'єкту (descriptors)
Представлення властивостей класу форм (банани,
яблука, груші, ..)
периметр, площа,
компактність, кривизна,
кількість кутів, отворів?
3

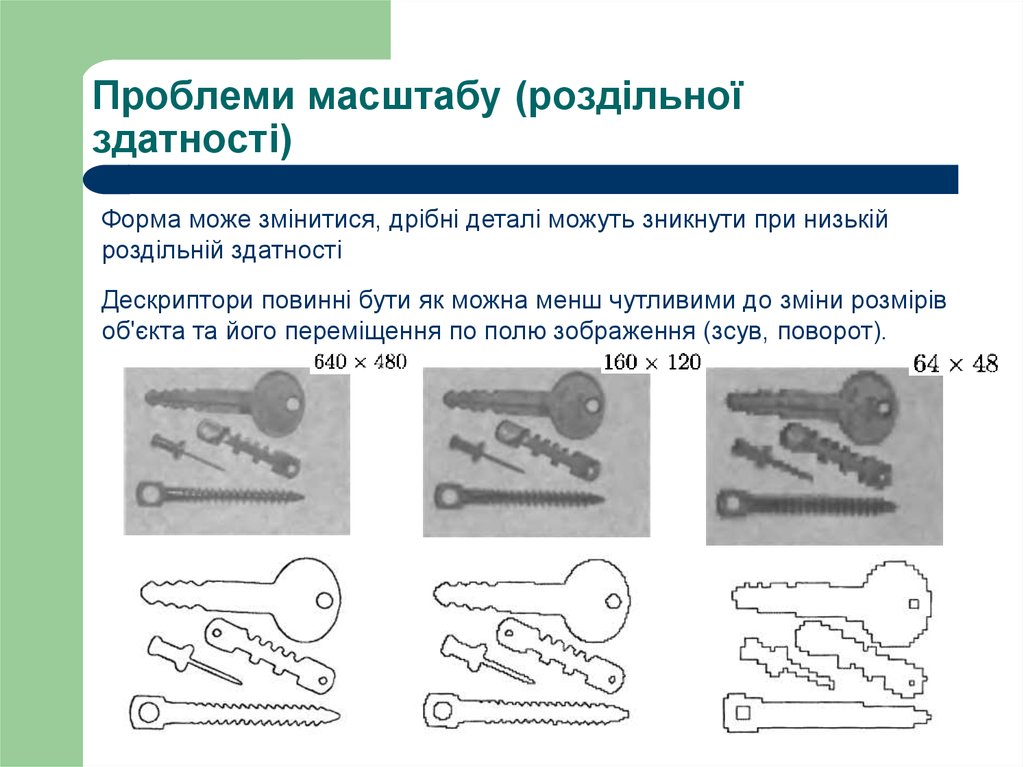
4. Проблеми масштабу (роздільної здатності)

Форма може змінитися, дрібні деталі можуть зникнути при низькій
роздільній здатності
Дескриптори повинні бути як можна менш чутливими до зміни розмірів
об'єкта та його переміщення по полю зображення (зсув, поворот).
4

5. Представлення

В параметричній формі
c(l)= (x(l), y(l))
(x0 , y0 )...(xN 1 , y N 1 )
кожна точка контуру об'єкта X може бути представлена через
параметр l - довжина дуги (шляху) arc length (path length), 0 l L
L – довжина контуру
x(l)
y(x)
l
y(l)
y=y(x)
x
c(l)= (x(l), y(l))
l
5

6. Представлення

параметрична форма в комплексній
площині
z(l)=(Re(z(l)), Im(z(l))
d d ( )
параметрична
форма в полярних
координатах
(l ) (d (l ), (l ))
6

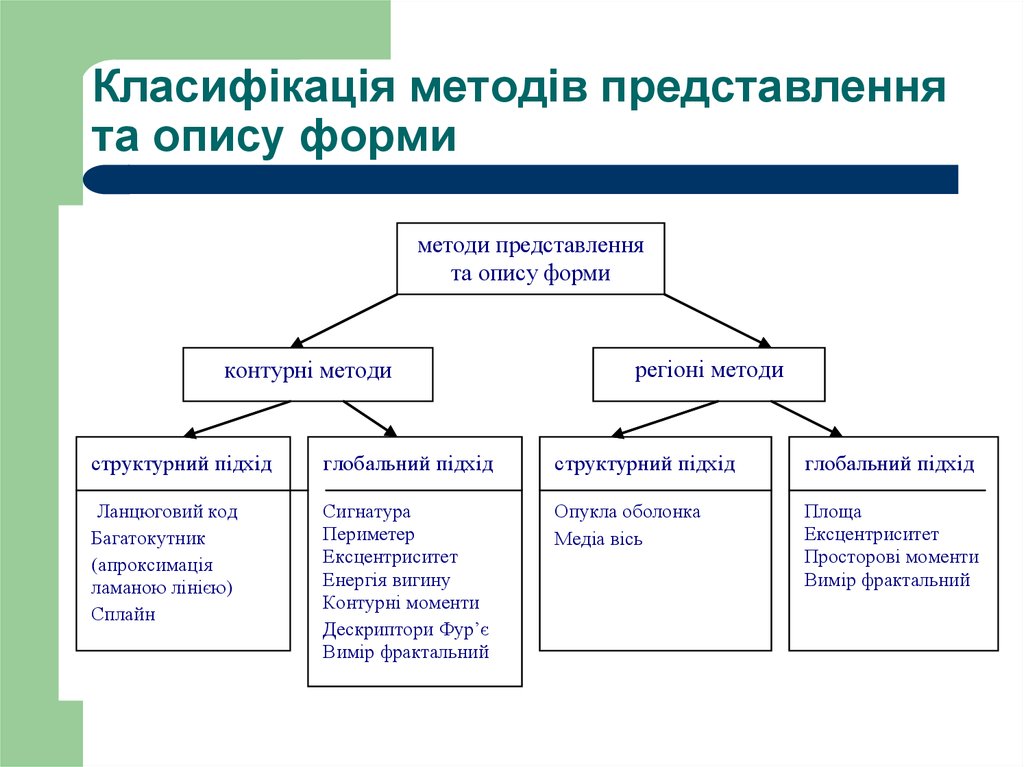
7. Класифікація методів представлення та опису форми

методи представлення
та опису форми
контурні методи
регіоні методи
структурний підхід
глобальний підхід
структурний підхід
глобальний підхід
Ланцюговий код
Багатокутник
(апроксимація
ламаною лінією)
Сплайн
Сигнатура
Периметер
Ексцентриситет
Енергія вигину
Контурні моменти
Дескриптори Фур’є
Вимір фрактальний
Опукла оболонка
Медіа вісь
Площа
Ексцентриситет
Просторові моменти
Вимір фрактальний
7

8. Класифікація методів представлення

Локальні методи представлення, забезпечують
доступ до точок контуру форми, дозволяють
знаходити специфічні, локальні характеристики
(ланцюговий код, сигнатура, багатокутник, опукла
оболонка, сплайн);
Глобальні методи представлення,
представляють форму в цілому, дозволяють
знаходити загальні характеристики (дескриптори
Фур'є; контурні, просторові моменти).
Медіальні (medial) методи представлення
поєднання локальних і глобальних властивостей
(серединні вісі, скелет).
8

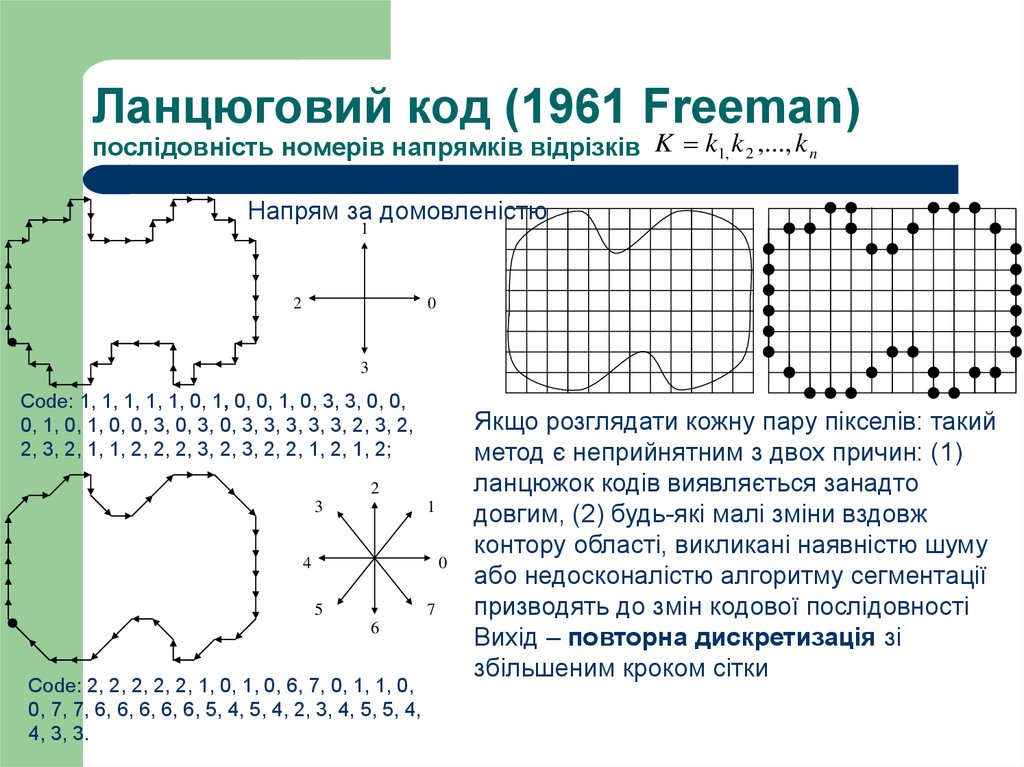
9. Ланцюговий код (1961 Freeman) послідовність номерів напрямків відрізків

K k1, k 2 ,..., k n
Напрям за домовленістю
1
2
0
3
Code: 1, 1, 1, 1, 1, 0, 1, 0, 0, 1, 0, 3, 3, 0, 0,
0, 1, 0, 1, 0, 0, 3, 0, 3, 0, 3, 3, 3, 3, 3, 2, 3, 2,
2, 3, 2, 1, 1, 2, 2, 2, 3, 2, 3, 2, 2, 1, 2, 1, 2;
2
3
1
4
0
5
7
6
Code: 2, 2, 2, 2, 2, 1, 0, 1, 0, 6, 7, 0, 1, 1, 0,
0, 7, 7, 6, 6, 6, 6, 6, 5, 4, 5, 4, 2, 3, 4, 5, 5, 4,
4, 3, 3.
Якщо розглядати кожну пару пікселів: такий
метод є неприйнятним з двох причин: (1)
ланцюжок кодів виявляється занадто
довгим, (2) будь-які малі зміни вздовж
контору області, викликані наявністю шуму
або недосконалістю алгоритму сегментації
призводять до змін кодової послідовності
Вихід – повторна дискретизація зі
збільшеним кроком сітки
9

10. Ланцюговий код (1961 Freeman)

Ланцюговий код (1961 Freeman)K k k ,..., k
1,
Ланцюговий код контору області
залежить від початкової точки тому код
розглядається як циклічна послідовність
номерів напрямків відрізків
diff (k i , k i 1 ) if i 1
di
i 1, 2, ... N
diff
(
k
,
k
)
if
i
1
Інваріантний щодо повороту замість
i
N
самого коду розглядають його першу
різницю
2
2
3
1
4
0
5
7
6
7
7
6
5
4
6
5
4
3
2
1
0
Code: 2, 2, 2, 2, 2, 1, 0, 1, 0, 6, 7, 0, 1,
1, 0, 0, 7, 7, 6, 6, 6, 6, 6, 5, 4, 5, 4, 2, 3,
4, 5, 5, 4, 4, 3, 3.
2
1
3
2
1
0
differential chain code: 5(-1), 0, 0, 0, 5, 5, 1, 5, 6, 1, 3,
1, 0, 5, 0, 7, 0, 5, 0, 0, 0, 0, 5, 5, 1, 5, 6, 1, 1, 1, 0, 5, 0,
5, 0;
4
3
0
2
-1
-2
Кривизна (Curvature) швидкість зміни кута нахилу: -1, 0,
0, 0, -1, -1, 1, -1, -2 (6), 1, 1, 1, 0, -1, 0, -1 (7), 0, -1, 0, 0, 0,
0, -1, -1, 1, -1, -2, 1, 1, 1, 0, -1, 0 -1, 0.
1
0
Сума квадратів дає енергію вигину (bending
energy) : 1, 0, 0, 0, 1, 1, 1, 1, 4, 1, 1, 10
1, 0, 1, 0, 1,
0, 1, 0, 0, 0, 0, 1, 1, 1, 1, 4, 1, 1, 1, 0, 1, 0, 1, 0
n

11. Багатокутник (Polygonal Approximations) (апроксимація ламаною лінією)

Границя може бути скільки завгодно точно наближений ламаною лінією. Якщо
границя замкнена, апроксимація є точною, коли число відрізків ламаної дорівнює
кількості точок границі.
Мета – за допомогою якомога меншої кількості відрізків наблизити
«найсуттєвіше» у формі границі. У загальному випадку ця задача
нетривіальна і її рішення часто виливається в трудомісткі переборний
схеми. Тим не менш, існують деякі методи апроксимації, які
характеризуються помірною обчислювальної складністю і добре підходять
для цифрової обробки зображень.
11

12. метод знаходження ламаної мінімальної довжини

Розглянемо границю області як гумову стрічку, що знаходиться між двома
стінками, які відповідають внутрішньої і зовнішньої границі ланцюжка
елементів.
При стягуванні стрічки вона прийме форму багатокутника з мінімальним
периметром, що відповідає геометричній формі даного ланцюжка
елементів. Якщо кожен елемент містить в собі єдину точку границі, то
величина відхилення фактичної границі від її наближення гумовою
стрічкою всередині будь-якого елемента не перевищує
де d - мінімальна відстань між пікселями, тобто крок дискретизації при
отримані вихідного цифрового зображення.
12

13. Методи злиття

• Засновані на застосуванні критерію середньої помилки або критерію
іншого виду.
• Відбувається об'єднання точок вздовж границі в одну пряму лінію до тих
пір, поки середньоквадратичне відхилення точок, що об'єднуються, від
прямої, що утворюється, не перевищить заздалегідь заданий поріг.
• Після цього параметри прямої запам'ятовуються і починається нове
об'єднання точок, що супроводжується побудовою нової прямої і новим
накопиченням помилки відхилення.
•Недолік – вершини отриманої ламаної лінії не завжди збігаються з
вигинами початкової границі. Наприклад, якщо зустрінеться кут, то до
попереднього відрізку буде додана ще якась (в залежності від порогу)
кількість точок за вершиною кута, перш ніж виявиться перевищення
порога. Однак, цей недолік можна зменшити, застосовуючи поряд зі
злиттям методи розбиття.
13

14. Методи розбиття

• Відрізок послідовно розбивається на дві частини (замінюється двома новими
відрізками), до тих пір, поки не почне виконуватися деякий заданий критерій.
• Наприклад, може бути поставлено таку вимогу, щоб максимум найкоротших
відстаней від відрізка прямої, що з'єднує дві точки границі, до проміжних точок
границі не перевищував встановленого порога. Якщо ця умова порушується, то
максимально віддалена від відрізка точка границі стає новою вершиною
апроксимуючої ламаної, а початковий відрізок ламаної замінюється двома
новими.
• Переваги методу – дозволяє виявляти найбільш помітні точки вигину або
зламу на границі об'єкта.
аb – початковий відрізок апроксимації границі, з'єднує найбільш віддалені точки. Точка с
– найбільш віддалена точка верхньої ділянки границі, точка d - найбільш віддалена точка
нижньої ділянки. Процедура розбиття з порогом, рівним 1/4 довжини відрізка аb. Оскільки
ні для одного з отриманих відрізків цей поріг (максимум найкоротших відстаней від точок
14
границі до відповідних відрізків) не перевищено, процедура завершується.

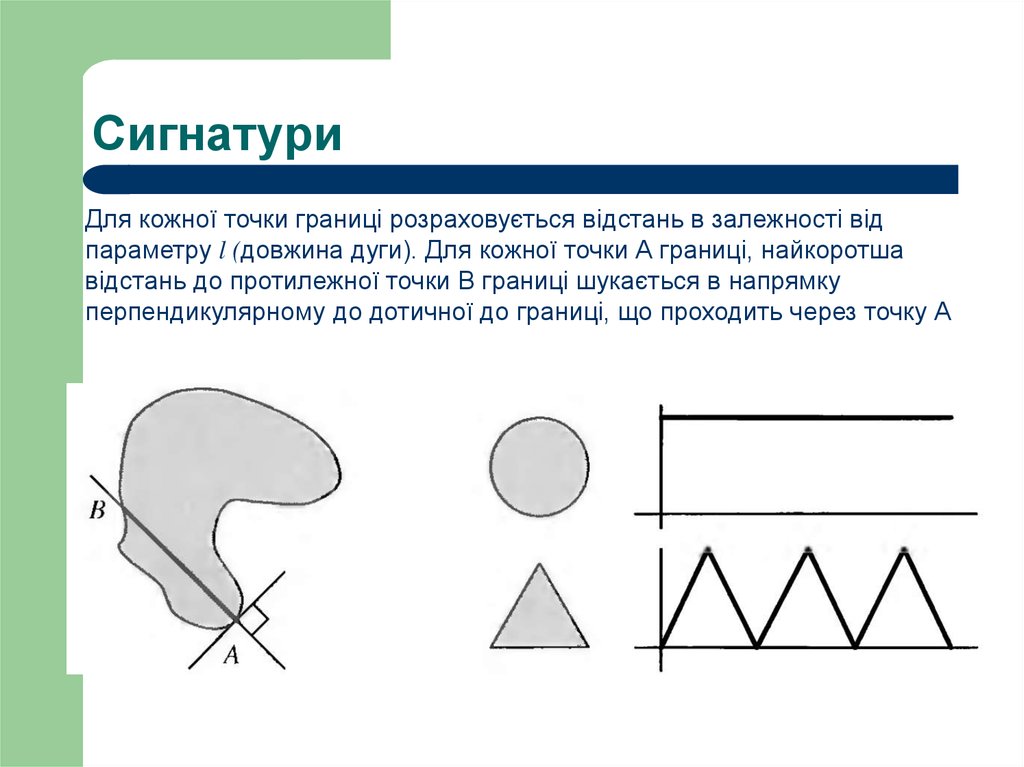
15. Сигнатури

Сигнатура – опис границі об'єкта за допомогою одномірної функції, яка
може будуватися різними способами. Описати легше, ніж вихідну
двовимірну границю.
Найпростіша “кут - відстань”, полягає в побудові залежності відстані від
центроїда (тобто від деякої середньої точки об'єкта, наприклад, його
центра ваги) до границі об'єкта у вигляді функції кута.
15

16. Сигнатури

Для кожної точки границі розраховується відстань в залежності від
параметру l (довжина дуги). Для кожної точки А границі, найкоротша
відстань до протилежної точки В границі шукається в напрямку
перпендикулярному до дотичної до границі, що проходить через точку А
16

17. Сигнатури

i
θi
Ri
P
Сигнатури
P
• Інваріантні по відношенню до паралельного переносу
• Залежать від повороту і зміни масштабу
• Інваріантність до повороту можна отримати, знайшовши спосіб вибору
однієї і тієї ж початкової точки для побудови сигнатури, незалежно від
орієнтації фігури.
Наприклад: (1) вибирати в якості початкової точки, максимально
віддалену від центроїда, якщо така точка буде єдиною і не залежить від
спотворень, що виникають при поворотах фігури.
(2) вибирати максимально віддалену від центроїда точку на власній осі
фігури. Метод вимагає більшого обсягу обчислень, але є більш стійким,
оскільки напрям власної осі фігури визначається з урахуванням усіх
точок її контуру.
• Ще один спосіб застосувати ланцюговий код границі, якщо вважати, що
кодування є досить грубим то поворот не порушить циклічності.
17

18. Розбиття границі на сегменти

• При такій декомпозиції зменшується складність границі і тим самим
спрощується процес її опису.
• Підхід привабливий, коли границя містить одну або кілька добре
виражених увігнутостей, що несуть інформацію про форму об'єкта. В
цьому випадку для декомпозиції границі використовується опукла
оболонка області, що знаходиться всередині границі.
• Множина називається опуклою якщо відрізок прямої, що з'єднує будьякі дві точки А, цілком лежить всередині А. Опукла оболонка Н
довільної множини S - це найменша опукла множина, що містить S.
Різниця множин Н \ S називається дефектом опуклості D множини S.
18

19. Розбиття границі на сегменти

Сегменти постійної кривизни (кути). Границя може бути поділена на
сегменти, які можуть бути представлені поліномами, як правило,
другого порядку, такі як кругові, еліптичні або параболічні сегменти.
Згладжування границі перед її
розбиттям.
(1) координати кожного пікселя
замінюються середніми
значеннями координат його сусідів.
Справляється з невеликими
нерівностями, важко піддається
контролю, відбувається зайве
згладжування, а малі значення
можуть виявитися недостатніми на
деяких ділянках.
(2) надійний спосіб – апроксимація
ламаною лінією
19

20. Остов області

• Представлення форми області будується шляхом зведення її до графа,
виділяючи остов області (серединні осі) за допомогою алгоритму стоншення
(скелетонізація).
• Побудова остова з використанням морфологічного підходу, не
передбачено жодних умов збереження зв'язності остова.
• Побудова остова за допомогою перетворення до головних осях (ПГО),
запропонував Блюм (Blum 1967).
• Наочне пояснення називається «пожежа в степу». Область зображення це степ,
рівномірно вкрита сухою травою, і припускають, що вся границя одночасно
загорається. Фронт пожежі поширюється всередину області з постійною
швидкістю. Результатом ПГО області буде множина точок, куди фронт вогню
доходить одночасно більш ніж з одного напрямку.
• Для кожної точки р області R знаходимо найближчу до неї точку на границі
В. Якщо таких точок більше однієї, то точка р лежить на серединній осі
області R (тобто остові). Поняття «найближчої» точки (і відповідне йому
ПГО) залежить від визначення відстані.
•алгоритми стоншення, поступово видаляються точки контуру області, при
умовах, що (1) вони не є кінцевими точками, (2) після видалення область
20
залишається зв'язною, і (3) це не призводить до зайвої ерозії області.

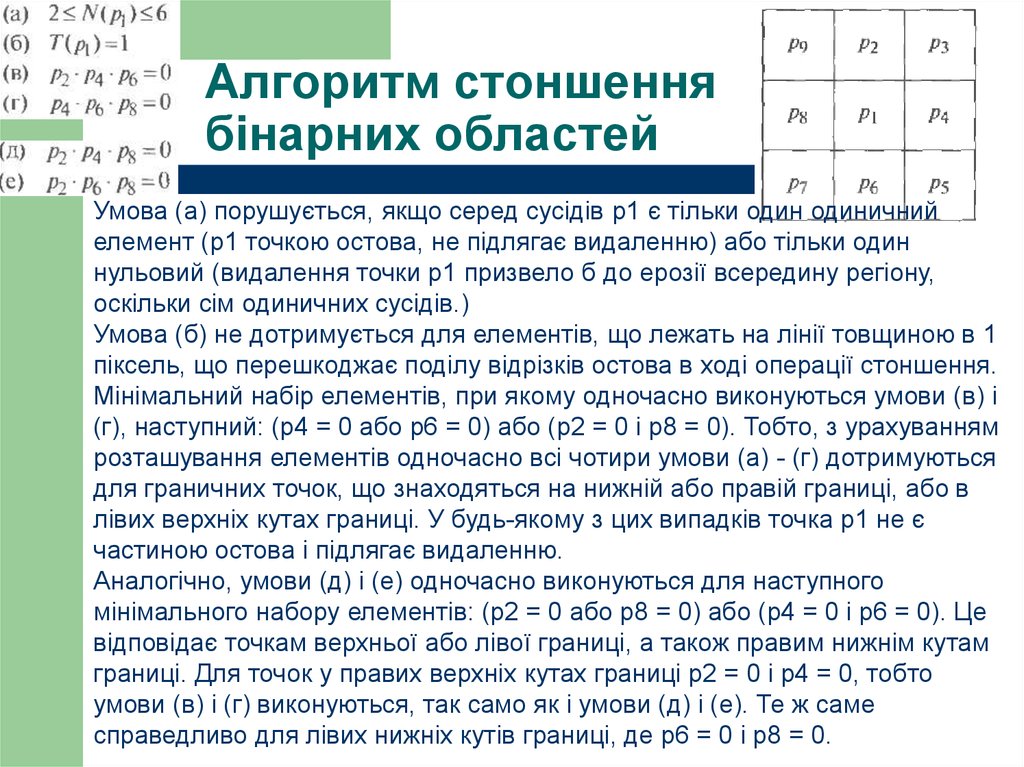
21. Алгоритм стоншення бінарних областей

Точки області мають значення 1, а точки фону - 0.
Послідовно застосовуємо два основних кроки до точок границі даної
області.
Граничною точкою є будь-який одиничний піксель, серед вісімки сусідів
якого є хоча б один елемент з нульовим значенням.
Перший крок алгоритму (з використанням наведених позначень для вісімки
сусідів) гранична точка р1 позначається для видалення, якщо виконуються
наступні умови:
Кількість не нульових сусідів
– число переходів 0-1 в
послідовності
При виконанні всіх умов елемент позначається для видалення, але саме
видалення не проводиться, поки не будуть оброблені всі точки кордону.
Така затримка запобігає зміні структури даних в процесі виконання
алгоритму. Після того, як перший крок виконаний для всіх точок границі,
21
відмічені елементи видаляються (значення змінюється на 0).

22. Алгоритм стоншення бінарних областей

Другий крок алгоритму умови (а) (б) залишаються додаються (д) (е).
Одна ітерація алгоритму стоншення складається з:
(1) застосування 1 кроку для всіх точок границі з позначенням кандидатів
на видалення, (2) видалення позначених точок, (3) застосування кроку 2 з
з позначенням кандидатів на видалення; (4) видалення позначених точок.
Повторюється до тих пір, поки не припиниться процес видалення точок.
22

23. Алгоритм стоншення бінарних областей

Умова (а) порушується, якщо серед сусідів p1 є тільки один одиничний
елемент (p1 точкою остова, не підлягає видаленню) або тільки один
нульовий (видалення точки p1 призвело б до ерозії всередину регіону,
оскільки сім одиничних сусідів.)
Умова (б) не дотримується для елементів, що лежать на лінії товщиною в 1
піксель, що перешкоджає поділу відрізків остова в ході операції стоншення.
Мінімальний набір елементів, при якому одночасно виконуються умови (в) і
(г), наступний: (р4 = 0 або p6 = 0) або (р2 = 0 і p8 = 0). Тобто, з урахуванням
розташування елементів одночасно всі чотири умови (а) - (г) дотримуються
для граничних точок, що знаходяться на нижній або правій границі, або в
лівих верхніх кутах границі. У будь-якому з цих випадків точка р1 не є
частиною остова і підлягає видаленню.
Аналогічно, умови (д) і (е) одночасно виконуються для наступного
мінімального набору елементів: (р2 = 0 або p8 = 0) або (р4 = 0 і p6 = 0). Це
відповідає точкам верхньої або лівої границі, а також правим нижнім кутам
границі. Для точок у правих верхніх кутах границі р2 = 0 і р4 = 0, тобто
умови (в) і (г) виконуються, так само як і умови (д) і (е). Те ж саме
23
справедливо для лівих нижніх кутів границі, де p6 = 0 і p8 = 0.

24. Побудова графа з остова

1. Позначимо точки остова: кінцева точка має тільки одного сусіда,
нормальна точка – два сусіда, вузлова точка – не менше трьох сусідів
остова.
2. Нехай вершинами-вузлами графа будуть всі кінцеві точки і вузлові
точки. З'єднати будь-яки дві вершини графа ребром, якщо вони пов'язані
послідовністю нормальних точок в регіоні остова.
24

25. Класифікація методів опису форми

Локальні дескриптори – дозволяють описати
структурні властивості форми (кривизна, кути
форми).
Глобальні дескриптори – дають загальну
інформацію, на основі властивостей форми,
(периметр, площа, компактність, енергія вигину,
ексцентриситет, дескриптори Фур‘є, фрактальна
розмірність).
Медіальні дескриптори: локальні (нормальна,
кінцева, вузлова точка, ширина форми), глобальні
(медіальна орієнтація, діаметр).
25

26. Прості дескриптори

Довжина – грубе наближення загальна кількість пікселів границі.
Для кривої, представленої ланцюговим кодом з одиничними кроками
дискретизації по обох напрямках, сума вертикальних, горизонтальних і
помножених 2 діагональних складових, дає точне значення довжини
контуру.
Периметр області – довжина контору.
N 1
P( X ) ( x(li 1 ) x(li )) 2 ( y (li 1 ) y (li )) 2
i 0
Площа області – кількість пікселів, що в ній містяться.
1
A( X )
2
N 1
x(l ) y(l y(l ) x(l )
i 0
i
i 1
i
i 1
Площа і периметр лише іноді і застосовуються як дескриптори, це
стосується тих випадків, коли розміри областей не змінюються.
26

27. Прості дескриптори

Компактність
C ( X ) P( X ) 2 / A( X )
• безрозмірна величина
• інваріантна до змін масштабу, зсуву та повороту
• приймає мінімальне значення для області круглої форми 4 12.57,
збільшується із зростанням складності форми
Залежність між площею і периметром
Ratio A( X ) / P( X )
27

28. Прості дескриптори

Діаметр
де D - міра відстані, рі, рj точки контуру
• направлення
• велика вісь контуру А
• мала вісь контору В визначається як
відрізок, перпендикулярний великої осі А
•базовий прямокутник проведений через кінці обох осей зі сторонами,
паралельними цим осям, повністю містить в собі весь контур.
• Ексцентриситет – відношення довжини великий осі до довжини малої
28

29. Кривизна контуру

x
Кривизна визначається як швидкість зміни кута нахилу.
d (l )
k (l )
dl
У загальному випадку важко надійно виміряти кривизну в деякій точці
дискретного контуру, тому що зазвичай є локальні нерівності
(«зазублини»).
Але, часто виявляється корисним використовувати різницю кутів нахилу
сусідніх сегментів контуру (наближення відрізками ламаної) як
дескриптори кривизни контуру в точці перетину цих відрізків.
d2y
d 2x
c(l)=(x(l), y(l)
dx y (l ) dy
x (l ) 2 y (l ) 2
x (l )
dl
dl
Позначення Ньютона
dl
dl
Функція кривизни загальне визначення k (l ) x(l ) y (l ) y (l ) x(l )
2
2 3/ 2
( x (l ) y (l ) )
Для кола радіуса r
x (l ) r cos(l ) y (l ) r sin( l ) x (l ) r sin( l )
k (l ) 1 / r
y (l ) r cos(l )
29

30. Алгоритм знаходження кривизни контуру S. Hermann and R. Klette 2003

Базується на аналізу двох векторів: forward (вперед) і backward (назад).
Контур c ( p1 ,..., pn ) точка pi ( xi , yi ) i 1,.., n 1 k n k обирається в
залежності від складності об'єкта
Для кожної точки p i в c визначаємо
the forward vector f i ,k pi pi k the backward vector bi ,k pi pi k індекси за
модулем n.
p i b
2
2
p i bi ,k d b ( xi k xi ) ( yi k yi )
Відстань від точки
до
Відстань від точки p i до p i f f i ,k d f ( xi k xi ) 2 ( yi k yi ) 2
Обраховуємо кути
xi k xi
xi k xi
f arctan y y
y
y
i
i k
i
i k
b arctan
(якщо у-різниця дорівнює нулю, застосувати arccot)
Кутова різниця f
i b / 2 f / 2
f i
Кривизна в точці p i
b b i
ki
f b
f (d b d f )
2d b d f
30

31. Кривизна контуру

• Опис за допомогою кривизни в точці можне бути уточнений за допомогою
ранжирування змін крутизни.
• Наприклад, точка р може вважатися частиною майже прямолінійного
відрізка контуру, якщо зміна кривизни не перевищує 10 °, або ж кутовий
точкою, якщо ця зміна більше 90 °.
• інтерпретація залежить від довжини окремих сегментів по відношенню до
загальної довжині кордону.
31

32. Енергія вигину

Енергія вигину – це необхідна енергія (збережена) для
трансформації кола до бажаної форми
Кривизна контуру k(l)
1 N 1
2
B( X ) k (li )
L i 0
32