Similar presentations:
Parametric Linear Programming
1. Parametric Linear Programming
Parametric LinearProgramming-1
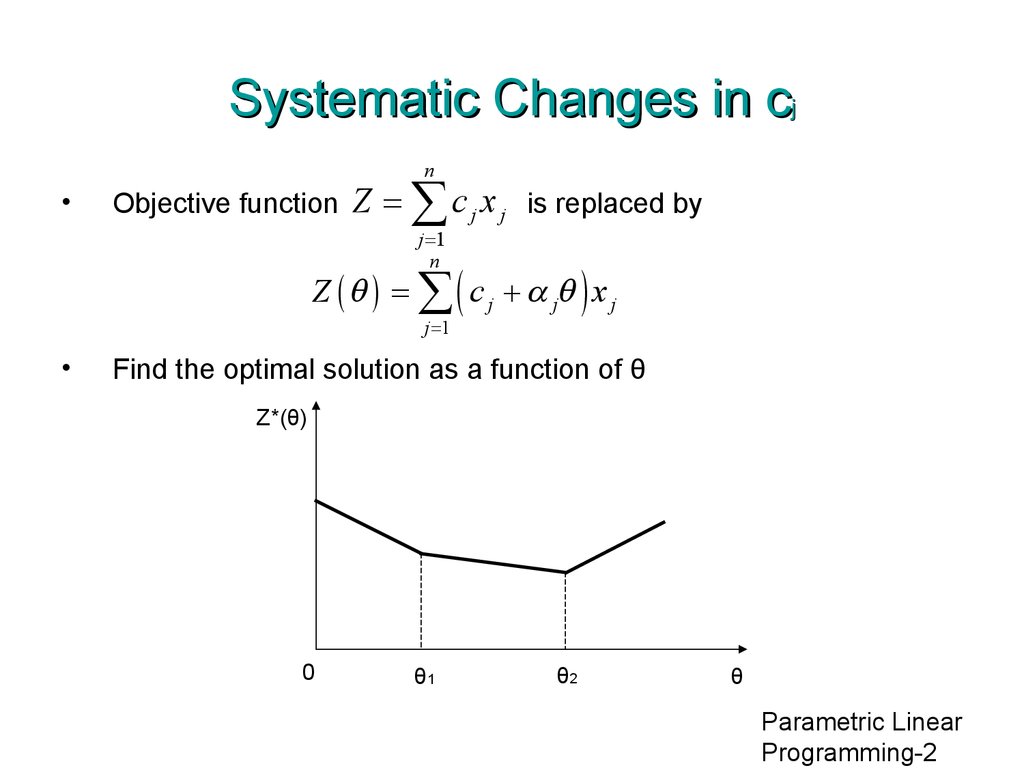
2. Systematic Changes in cj
nObjective function
Z = å c j x j is replaced by
j =1
n
Z ( q ) = å ( c j + a jq ) x j
j =1
Find the optimal solution as a function of θ
Z*(θ)
0
θ1
θ2
θ
Parametric Linear
Programming-2
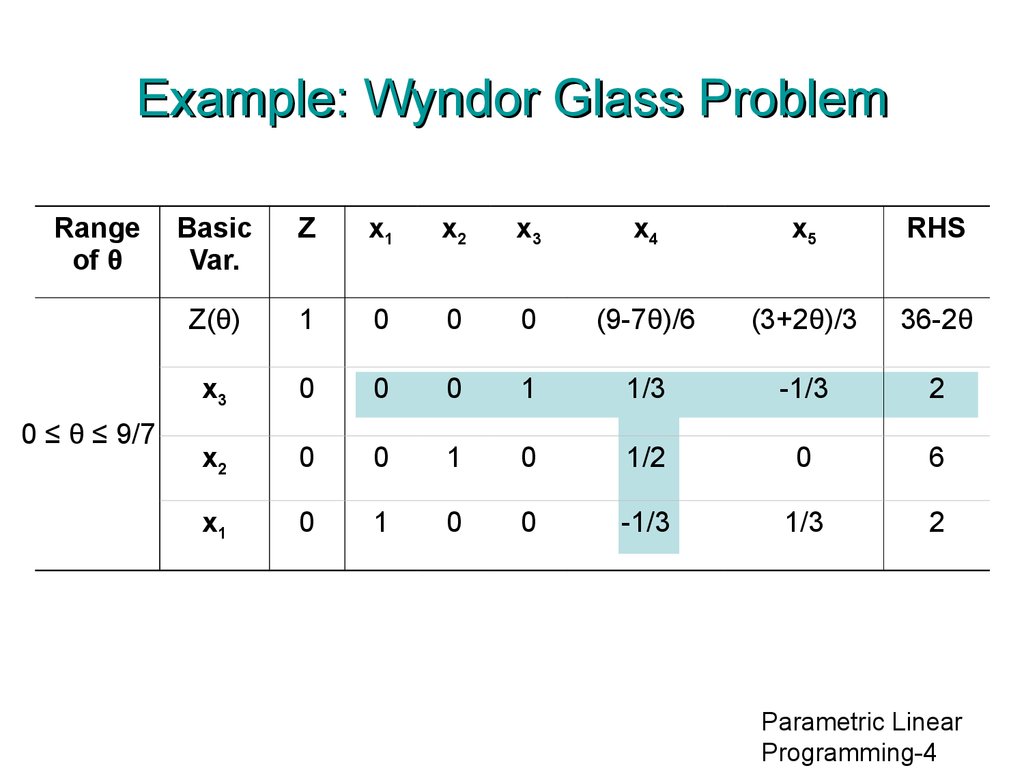
3. Example: Wyndor Glass Problem
• Z(θ) = (3 + 2θ) x1+(5 - θ) x2Parametric Linear
Programming-3
4. Example: Wyndor Glass Problem
Rangeof θ
0 ≤ θ ≤ 9/7
Basic
Var.
Z
x1
x2
x3
x4
x5
RHS
Z(θ)
1
0
0
0
(9-7θ)/6
(3+2θ)/3
36-2θ
x3
0
0
0
1
1/3
-1/3
2
x2
0
0
1
0
1/2
0
6
x1
0
1
0
0
-1/3
1/3
2
Parametric Linear
Programming-4
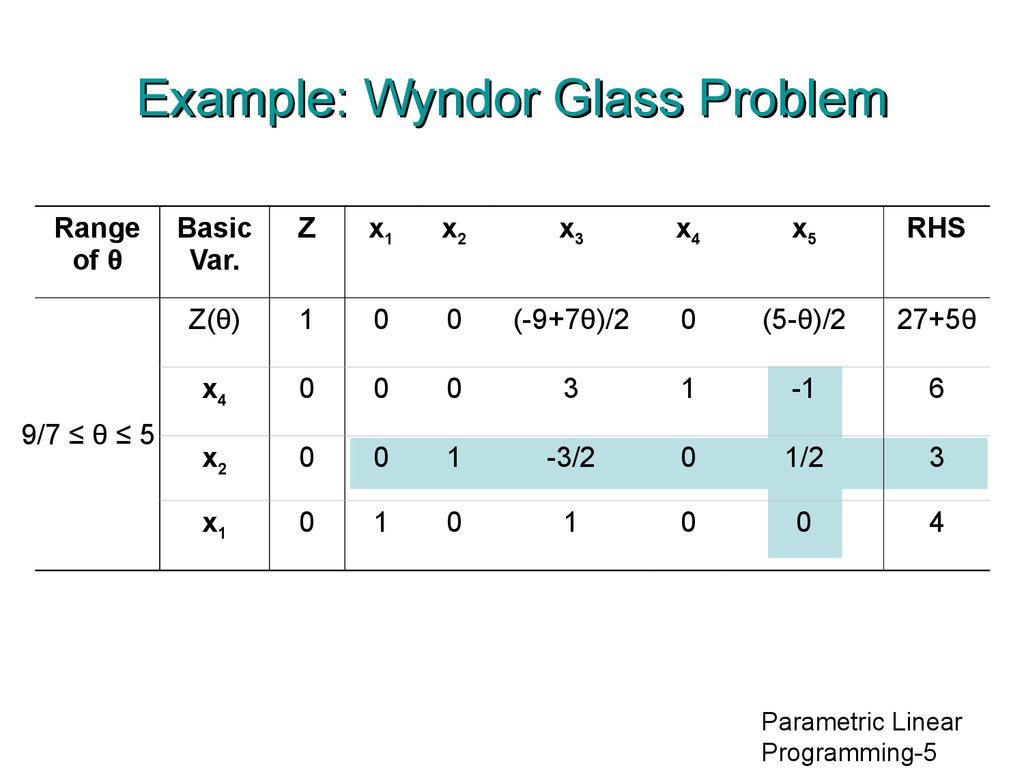
5. Example: Wyndor Glass Problem
Rangeof θ
9/7 ≤ θ ≤ 5
Basic
Var.
Z
x1
x2
x3
x4
x5
RHS
Z(θ)
1
0
0
(-9+7θ)/2
0
(5-θ)/2
27+5θ
x4
0
0
0
3
1
-1
6
x2
0
0
1
-3/2
0
1/2
3
x1
0
1
0
1
0
0
4
Parametric Linear
Programming-5
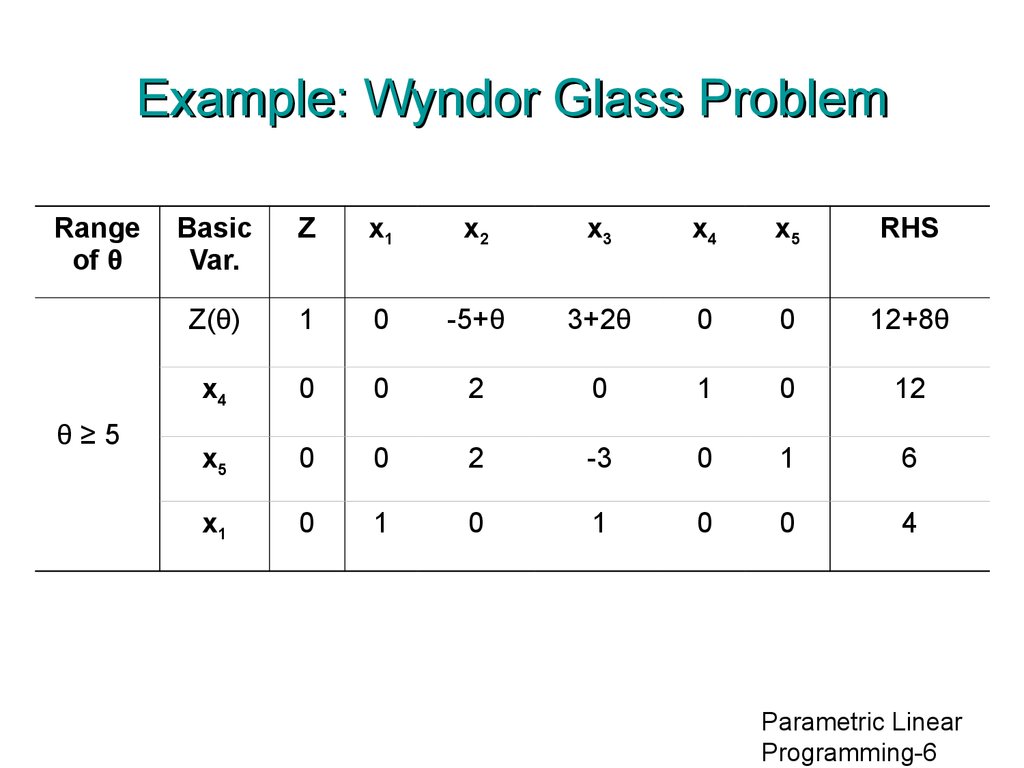
6. Example: Wyndor Glass Problem
Rangeof θ
θ≥5
Basic
Var.
Z
x1
x2
x3
x4
x5
RHS
Z(θ)
1
0
-5+θ
3+2θ
0
0
12+8θ
x4
0
0
2
0
1
0
12
x5
0
0
2
-3
0
1
6
x1
0
1
0
1
0
0
4
Parametric Linear
Programming-6
7. Procedure Summary for Systematic Changes in cj
1. Solve the problem with θ = 0 by the simplex method.2. Use the sensitivity analysis procedure to introduce the
Δcj = αjθ changes into Eq.(0).
3. Increase θ until one of the nonbasic variables has its
coefficient in Eq.(0) go negative (or until θ has been
increased as far as desired).
4. Use this variable as the entering basic variable for an
iteration of the simplex method to find the new optimal
solution. Return to Step 3.
Parametric Linear
Programming-7
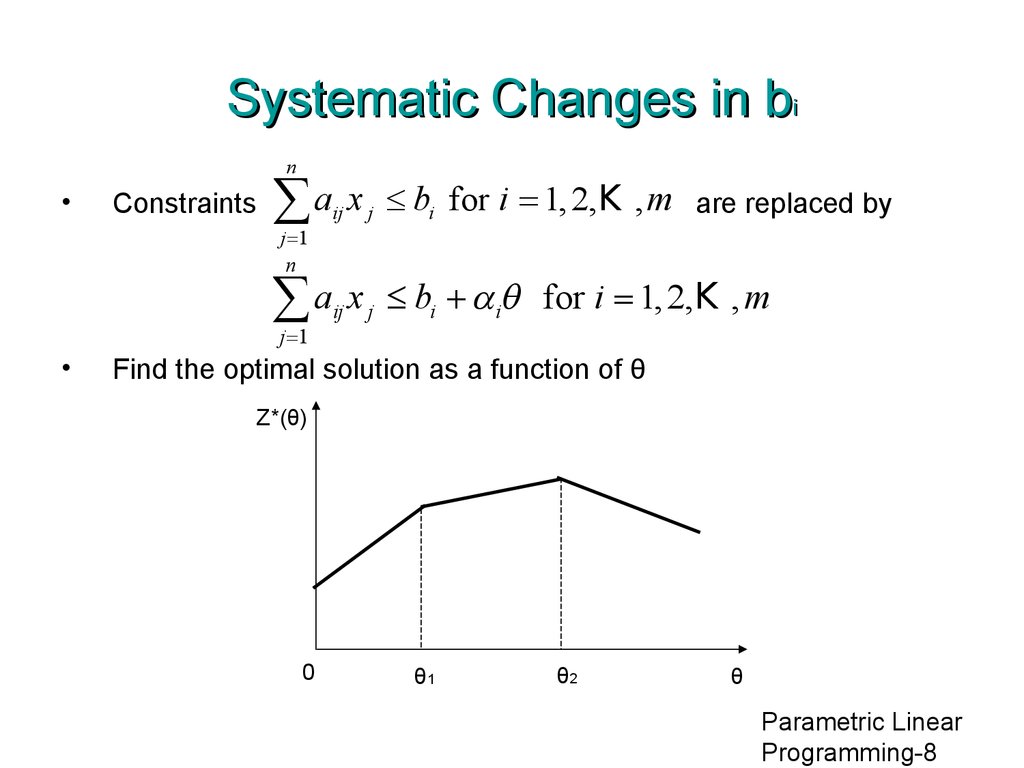
8. Systematic Changes in bi
nConstraints
åa x
j
£ bi for i = 1, 2,K , m
åa x
j
£ bi + aiq for i = 1, 2,K , m
j =1
n
j =1
ij
ij
are replaced by
Find the optimal solution as a function of θ
Z*(θ)
0
θ1
θ2
θ
Parametric Linear
Programming-8
9. Example: Wyndor Glass Problem
• y1+ 3y3 ≥ 3 + 2θ
2y2 + 2y3 ≥ 5 - θ
Parametric Linear
Programming-9
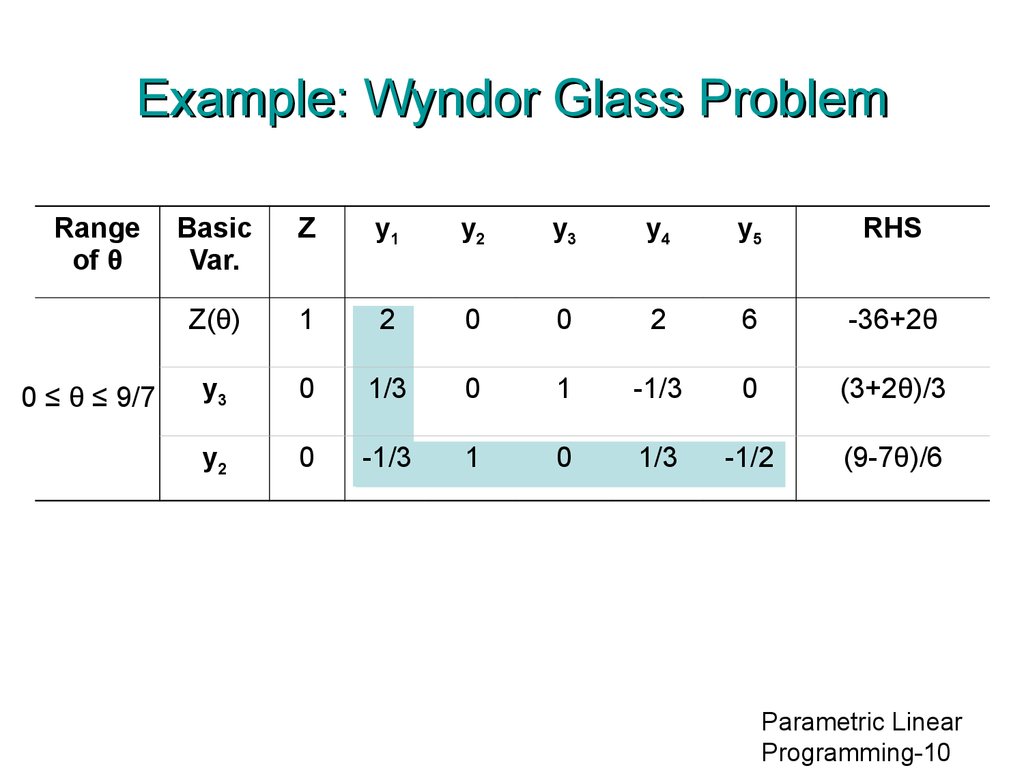
10. Example: Wyndor Glass Problem
Rangeof θ
0 ≤ θ ≤ 9/7
Basic
Var.
Z
y1
y2
y3
y4
y5
RHS
Z(θ)
1
2
0
0
2
6
-36+2θ
y3
0
1/3
0
1
-1/3
0
(3+2θ)/3
y2
0
-1/3
1
0
1/3
-1/2
(9-7θ)/6
Parametric Linear
Programming-10
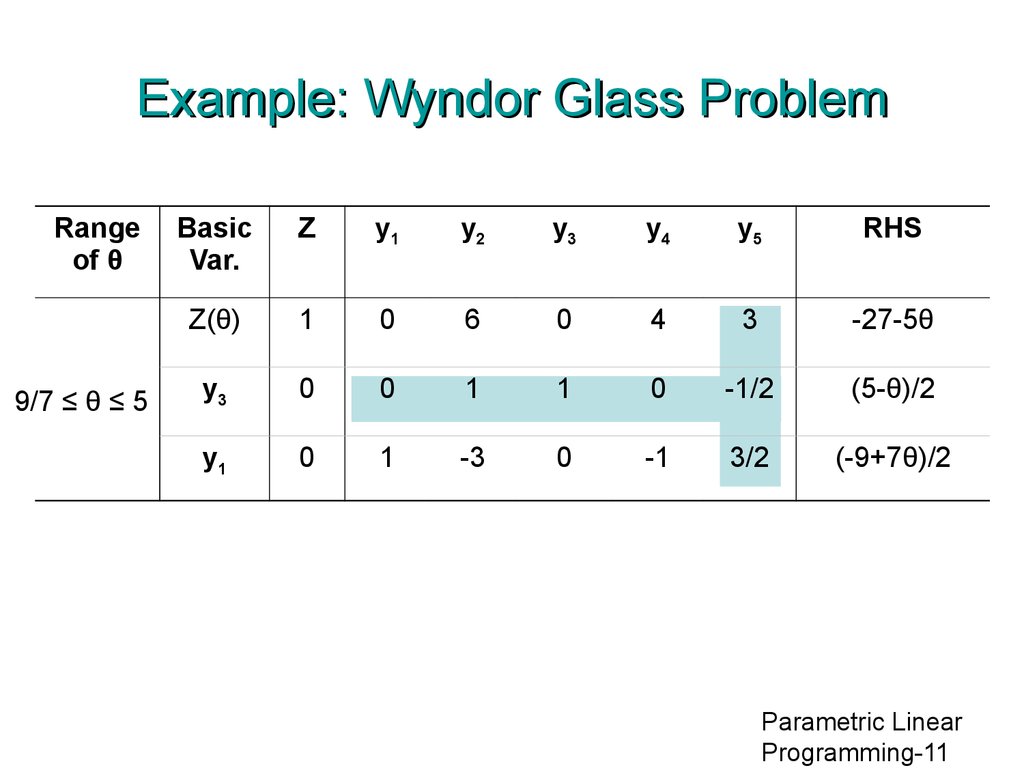
11. Example: Wyndor Glass Problem
Rangeof θ
9/7 ≤ θ ≤ 5
Basic
Var.
Z
y1
y2
y3
y4
y5
RHS
Z(θ)
1
0
6
0
4
3
-27-5θ
y3
0
0
1
1
0
-1/2
(5-θ)/2
y1
0
1
-3
0
-1
3/2
(-9+7θ)/2
Parametric Linear
Programming-11
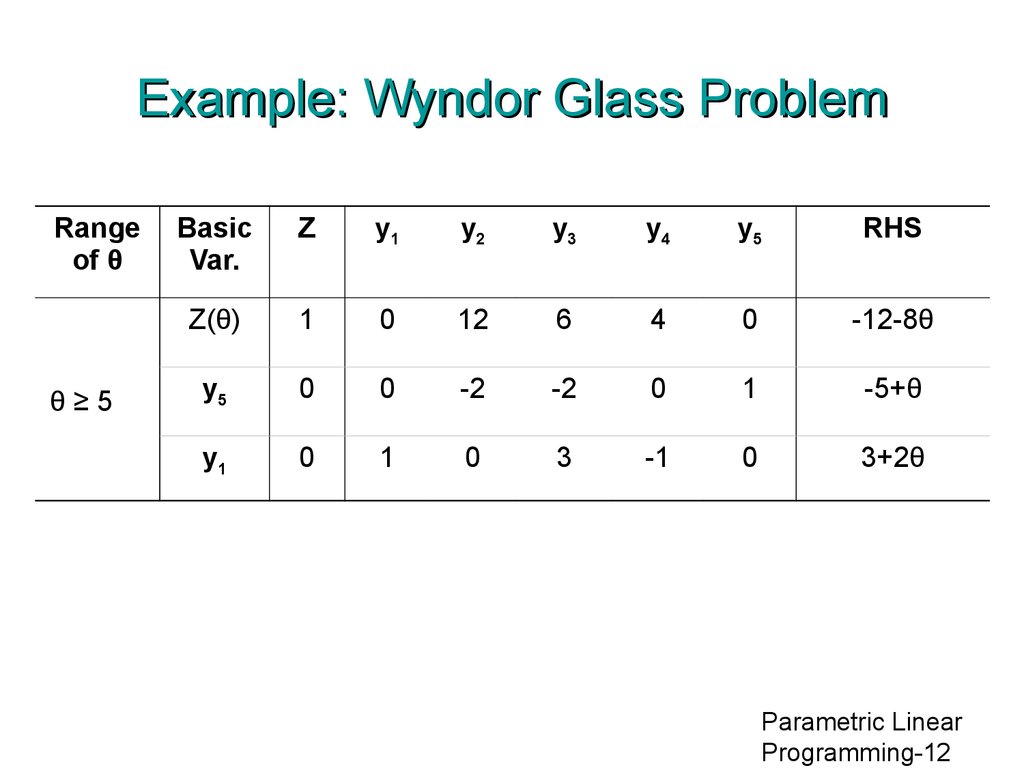
12. Example: Wyndor Glass Problem
Rangeof θ
θ≥5
Basic
Var.
Z
y1
y2
y3
y4
y5
RHS
Z(θ)
1
0
12
6
4
0
-12-8θ
y5
0
0
-2
-2
0
1
-5+θ
y1
0
1
0
3
-1
0
3+2θ
Parametric Linear
Programming-12
13. Procedure Summary for Systematic Changes in bi
1. Solve the problem with θ = 0 by the simplex method.2. Use the sensitivity analysis procedure to introduce the
Δbi = αiθ changes to the right side column.
3. Increase θ until one of the basic variables has its value
in the right side column go negative (or until θ has been
increased as far as desired).
4. Use this variable as the leaving basic variable for an
iteration of the dual simplex method to find the new
optimal solution. Return to Step 3.
Parametric Linear
Programming-13





 mathematics
mathematics programming
programming








