Медианы, биссектрисы и высоты треугольника

1. МЕДИАНЫ, БИССЕКТРИСЫ И ВЫСОТЫ ТРЕУГОЛЬНИКА

.

2. Перпендикуляр к прямой

А а, АН а
Отрезок АН называется
перпендикуляром,
проведенным из точки
А к прямой а, если
прямые АН и а
перпендикулярны.

3. Высота треугольника

Перпендикуляр,
АН СВ
проведенный из
вершины
треугольника к
прямой, содержащей
противоположную
сторону, называется
высотой
АН – высота треугольника
треугольника.

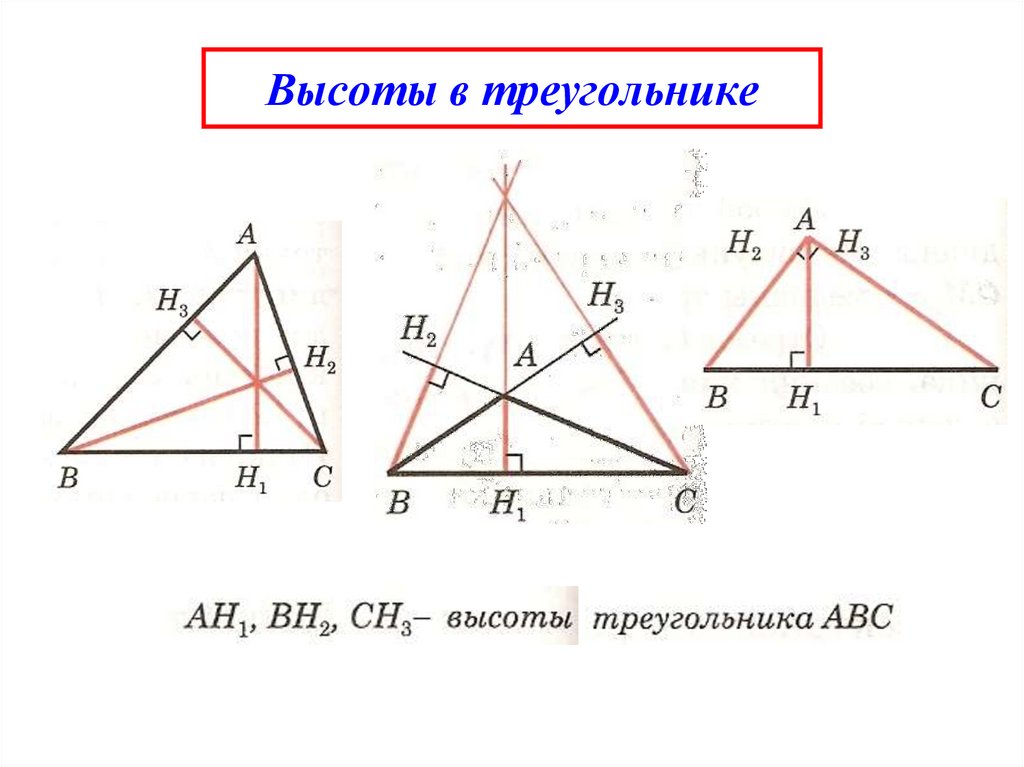
4. Высоты в треугольнике

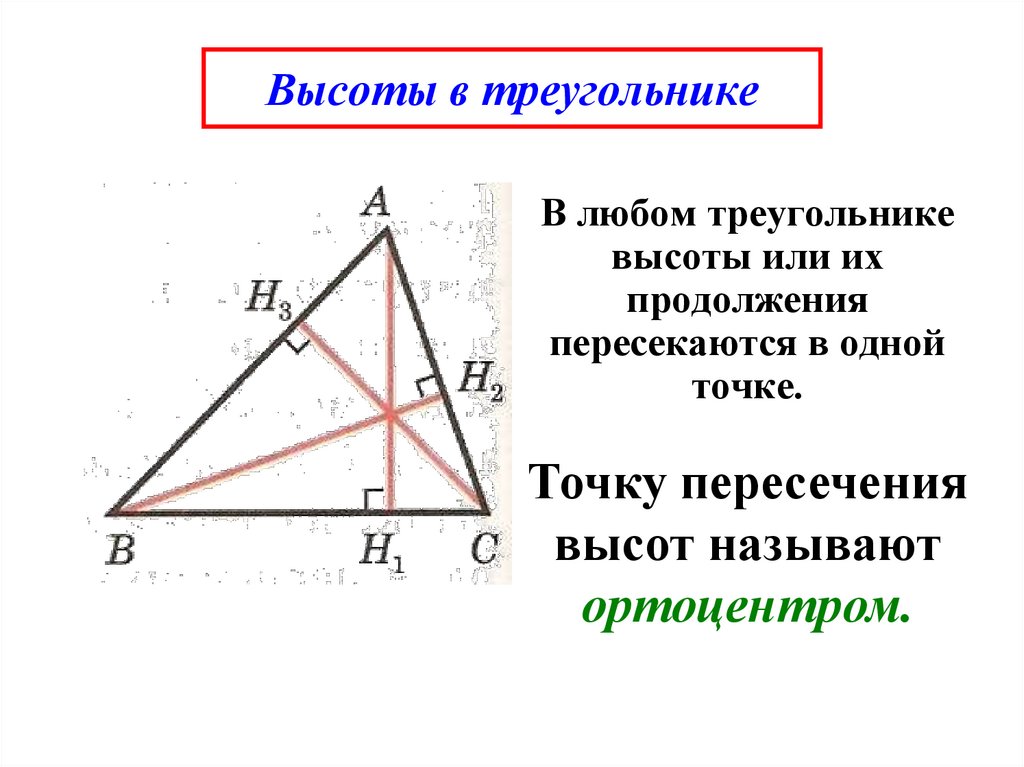
5. Высоты в треугольнике

В любом треугольнике
высоты или их
продолжения
пересекаются в одной
точке.
Точку пересечения
высот называют
ортоцентром.

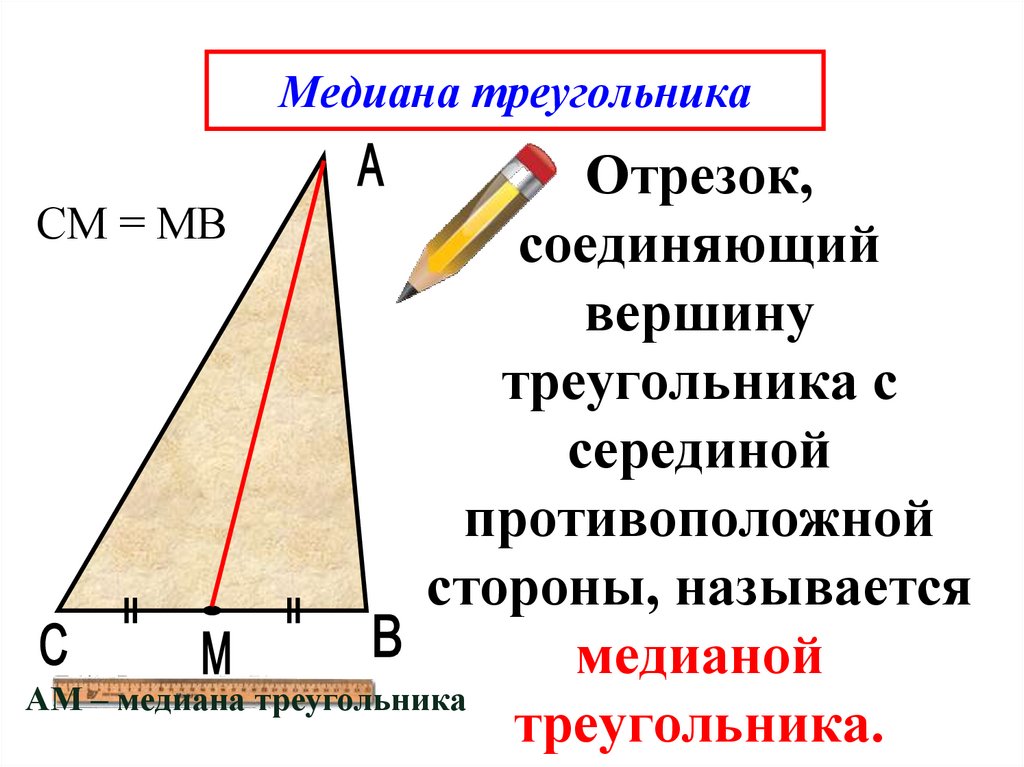
6. Медиана треугольника

Отрезок,
СМ = МВ
соединяющий
вершину
треугольника с
серединой
противоположной
стороны, называется
медианой
АМ – медиана треугольника
треугольника.

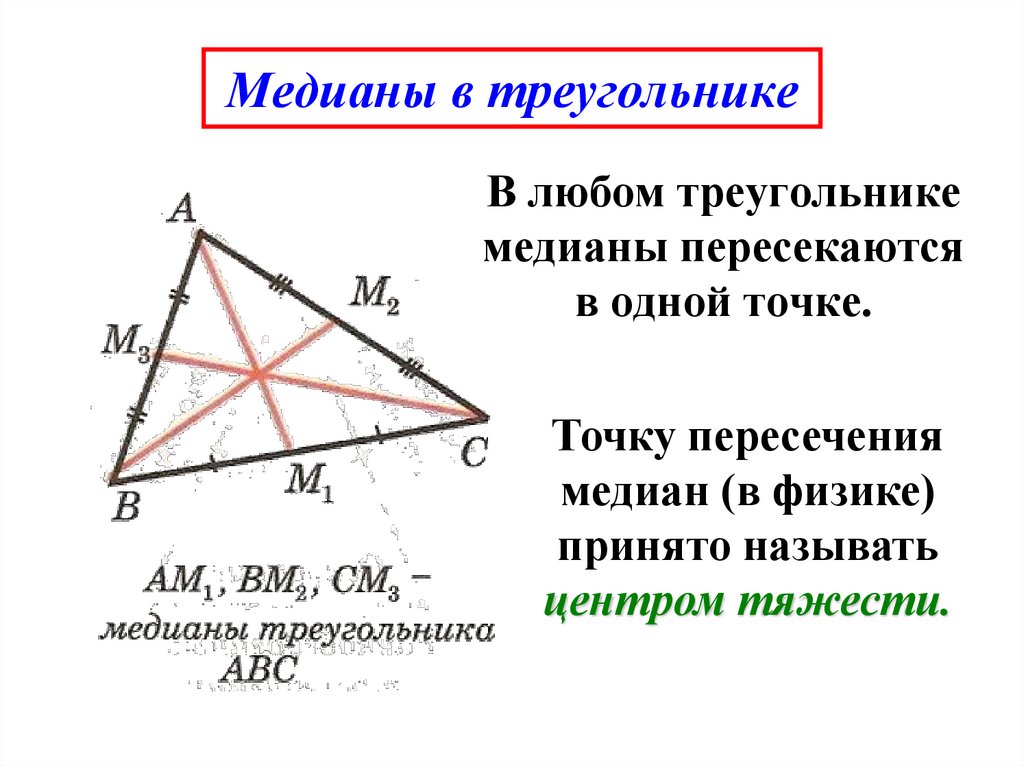
7. Медианы в треугольнике

В любом треугольнике
медианы пересекаются
в одной точке.
Точку пересечения
медиан (в физике)
принято называть
центром тяжести.

8. Биссектриса треугольника

АСА = ВАА
Отрезок биссектрисы
угла треугольника,
соединяющий вершину
треугольника с точкой
противоположной
стороны, называется
биссектрисой
треугольника.
АА1 – биссектриса треугольника

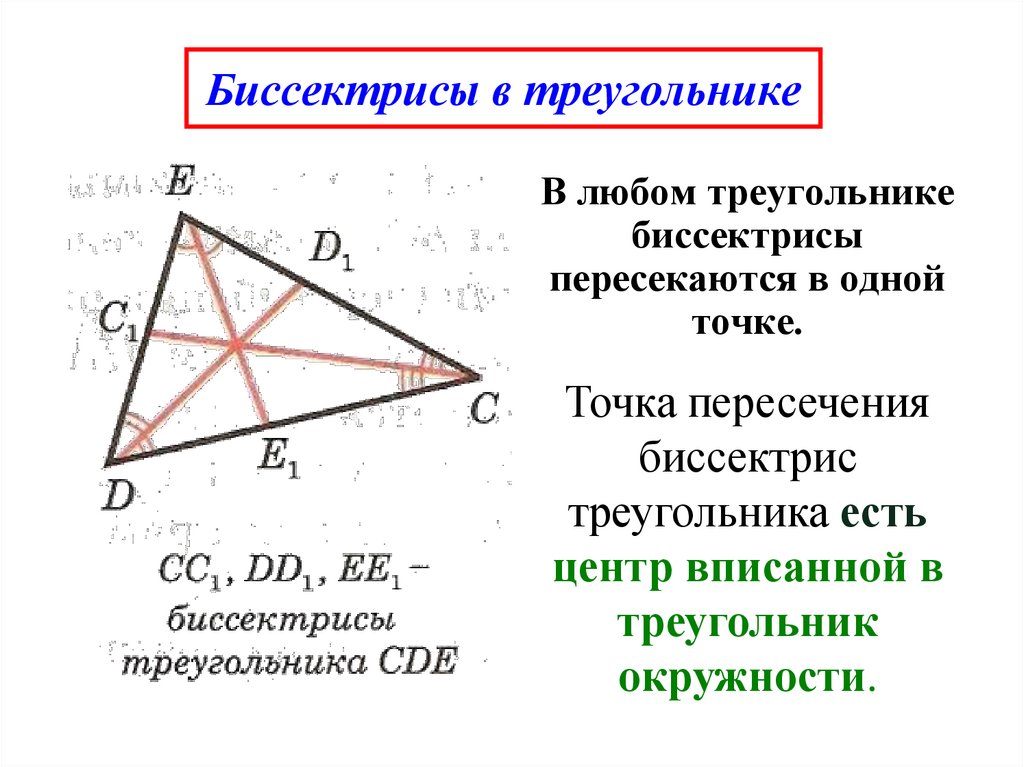
9. Биссектрисы в треугольнике

В любом треугольнике
биссектрисы
пересекаются в одной
точке.
Точка пересечения
биссектрис
треугольника есть
центр вписанной в
треугольник
окружности.

10.

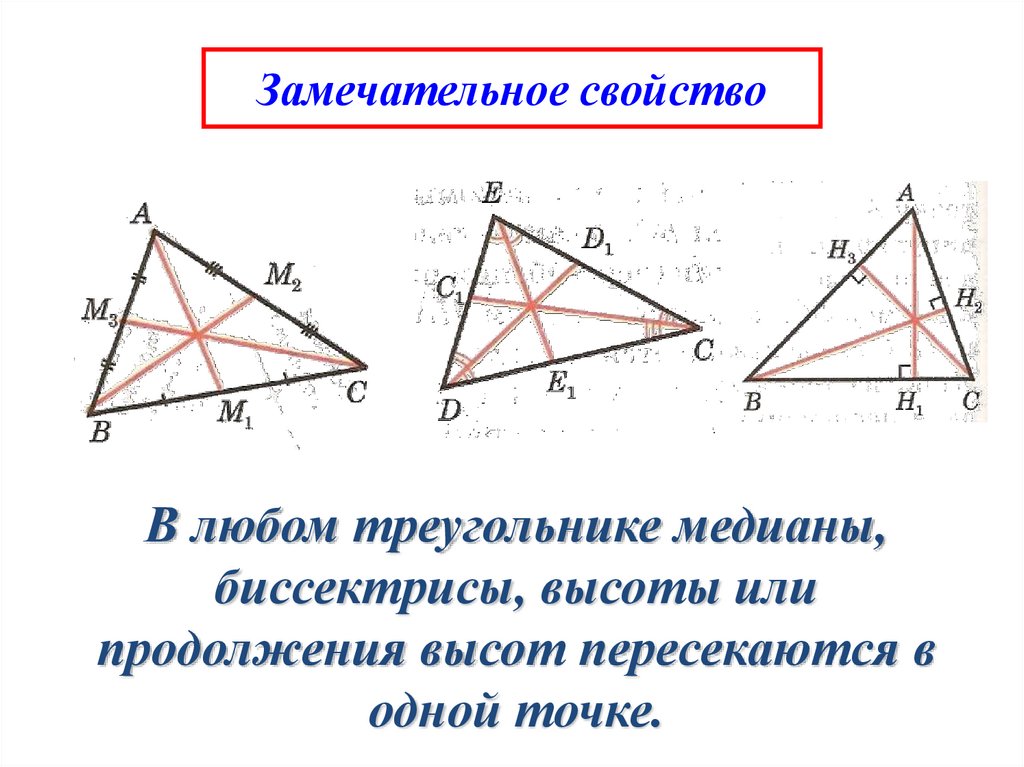
Замечательное свойство
В любом треугольнике медианы,
биссектрисы, высоты или
продолжения высот пересекаются в
одной точке.

11.

Решение задач
1) В ∆ВЕК к стороне ВК, равной 8 см,
проведена медиана ЕМ. Найти длину
отрезка МВ.
2) В ∆АВС проведена биссектриса СD. Чему
равна градусная мера ∠ACD, если ∠АСВ
= 80º?
3) В ∆КМО проведена высота КН. Чему
равна градусная мера ∠КНО?
Определить вид ∆КНО.

12.

Решение задач
4) В ∆ МРК ∠М=∠Р, РС – медиана.
Найти длину КР, если МС = 9,6 см.
М
5)
О
К
ОН и ОN – высоты
Е
треугольников МОК и
ЕОF, ОН = ОF. Найти
длину МК, если ЕN =
F 7,8 см, ОЕ = 8,6 см,
НМ = 6,3 см.

13.

Домашнее задание
• Стр. 41, № 19, все три пункта
оформить на листе формата А4.
• Стр. 34, пункт 25 – учить.

14.

19 (1)
19 (2)
19 (3)