Пропорциональные отрезки в прямоугольном треугольнике. Признаки подобия треугольников

1. Пропорциональные отрезки в прямоугольном треугольнике

2. Признаки подобия треугольников

1. По двум углам
2. По двум пропорциональным сторонам и
равному углу между ними
3. По трем пропорциональным сторонам

3.

4.

5. Определение

Отрезок XY называется средним
пропорциональным (или средним
геометрическим) для отрезков AB и CD, если
XY AB CD
Отрезок XY - среднее пропорциональное (среднее
геометрическое ) для отрезков AB и CD.

6.

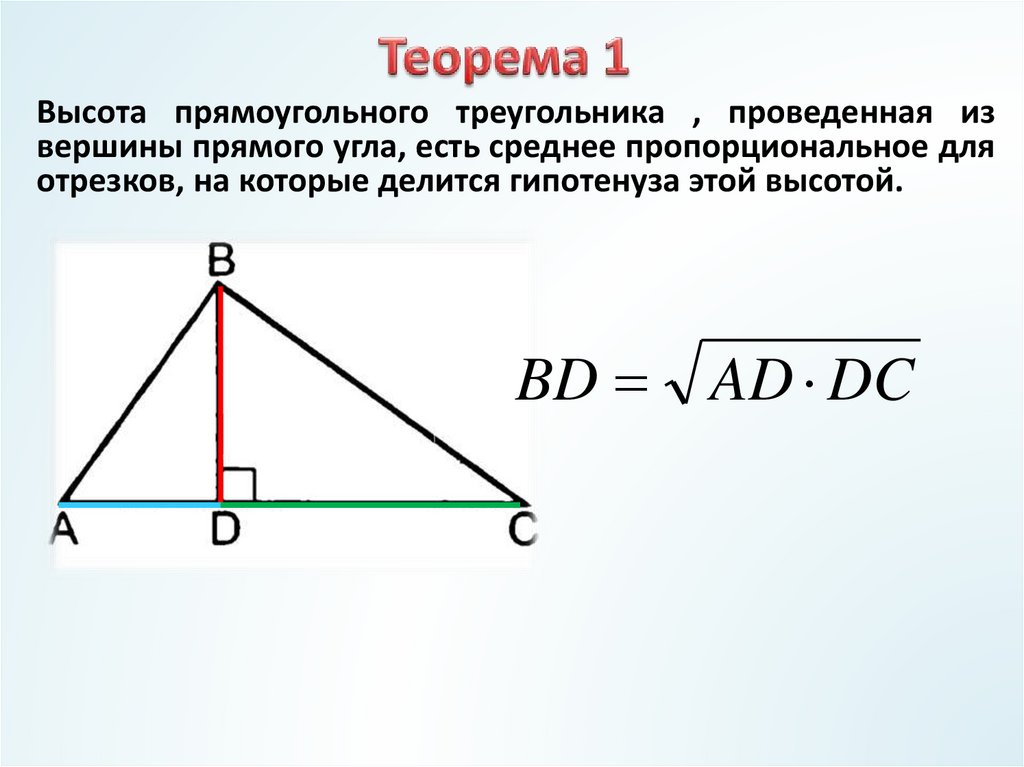
7. Теорема 1

Высота прямоугольного треугольника , проведенная из
вершины прямого угла, есть среднее пропорциональное для
отрезков, на которые делится гипотенуза этой высотой.
BD AD DC

8.

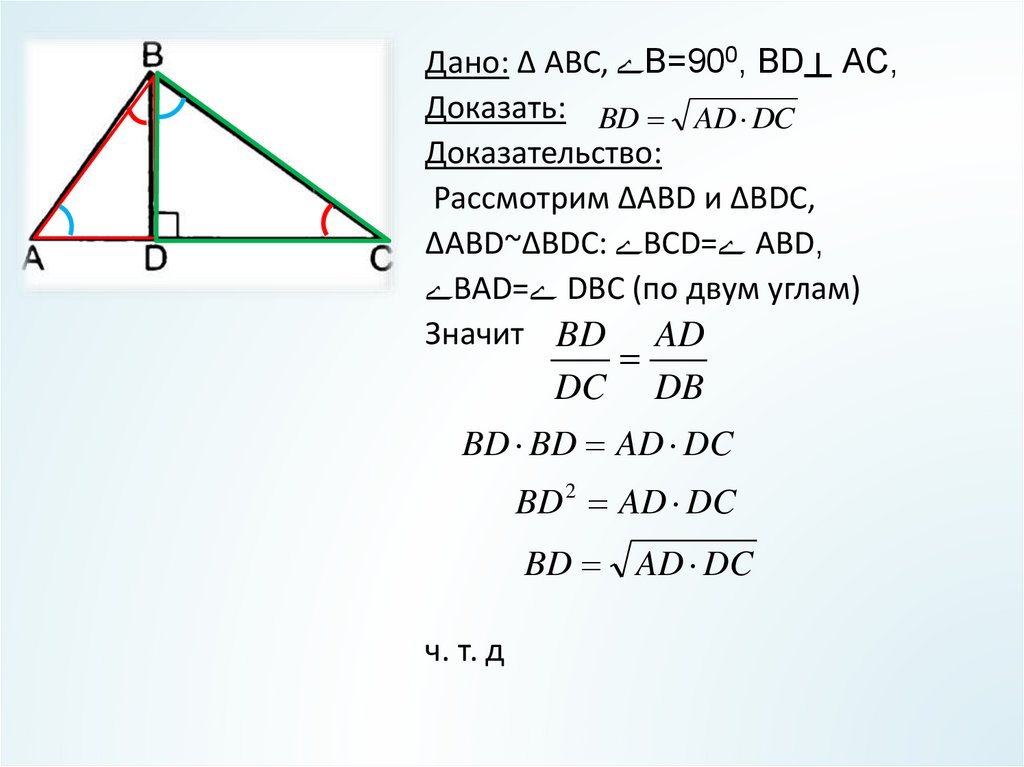
Дано: Δ ABC, ‫ے‬В=900, BD┴ AC,
Доказать: BD AD DC
Доказательство:
Рассмотрим ΔABD и ΔBDС,
ΔABD~ΔBDС: ‫ے‬BСD=‫ ے‬ABD,
‫ے‬BAD=‫ ے‬DBC (по двум углам)
Значит BD AD
DC
DB
BD BD AD DC
BD 2 AD DC
BD AD DC
ч. т. д

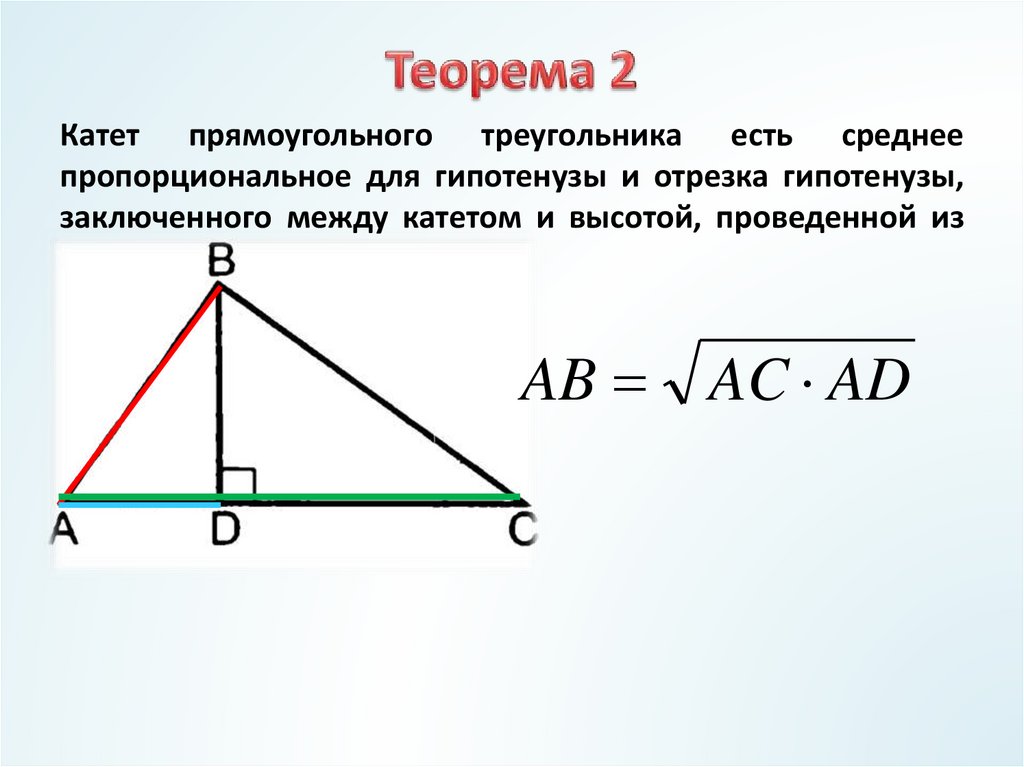
9. Теорема 2

Катет прямоугольного треугольника есть среднее
пропорциональное для гипотенузы и отрезка гипотенузы,
заключенного между катетом и высотой, проведенной из
вершины прямого угла
AB AC AD

10.

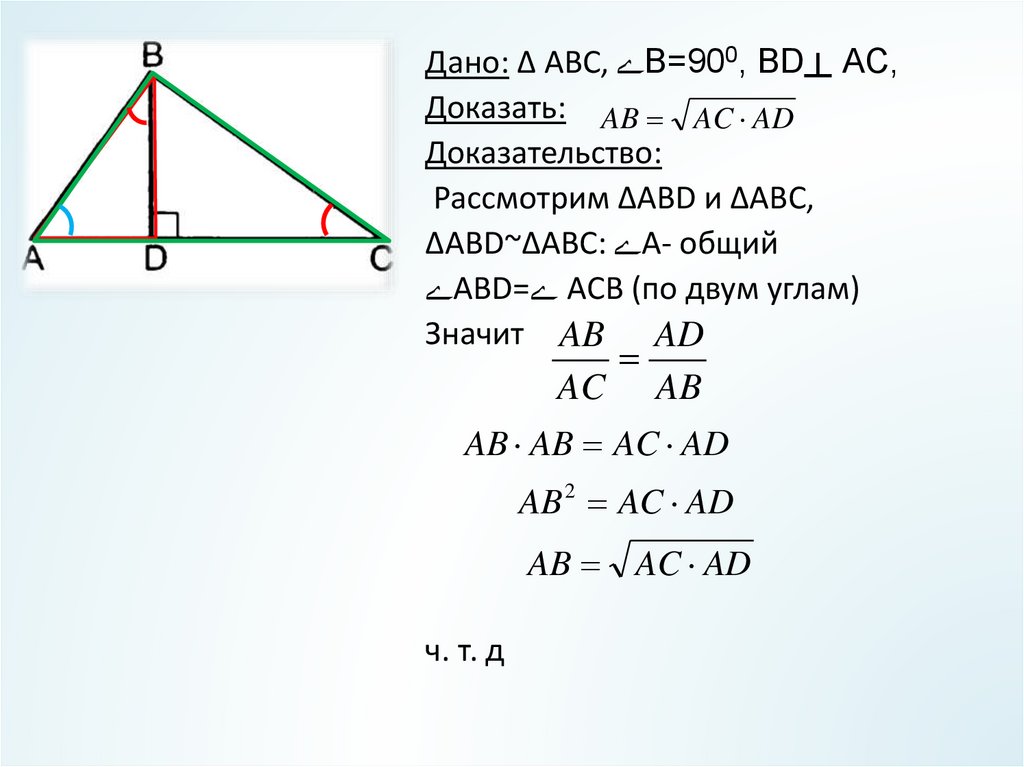
Дано: Δ ABC, ‫ے‬В=900, BD┴ AC,
Доказать: AB AC AD
Доказательство:
Рассмотрим ΔABD и ΔАBС,
ΔABD~ΔАBС: ‫ے‬A- общий
‫ے‬ABD=‫ ے‬АCB (по двум углам)
Значит AB AD
AC
AB
AB AB AC AD
AB 2 AC AD
AB AC AD
ч. т. д

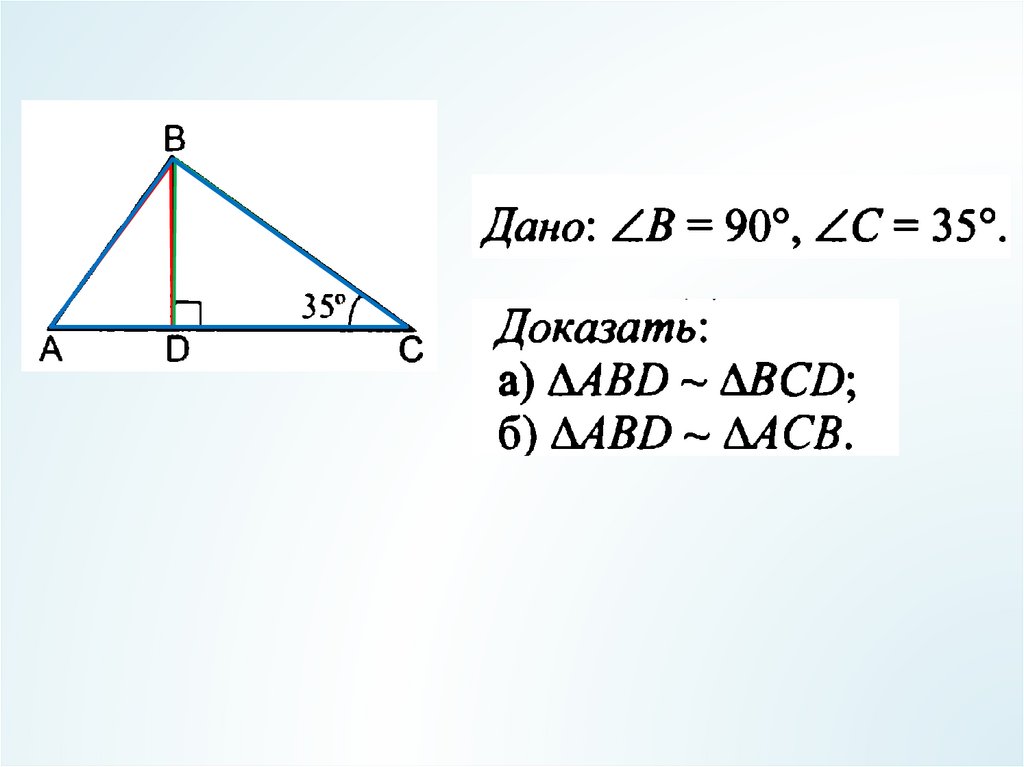
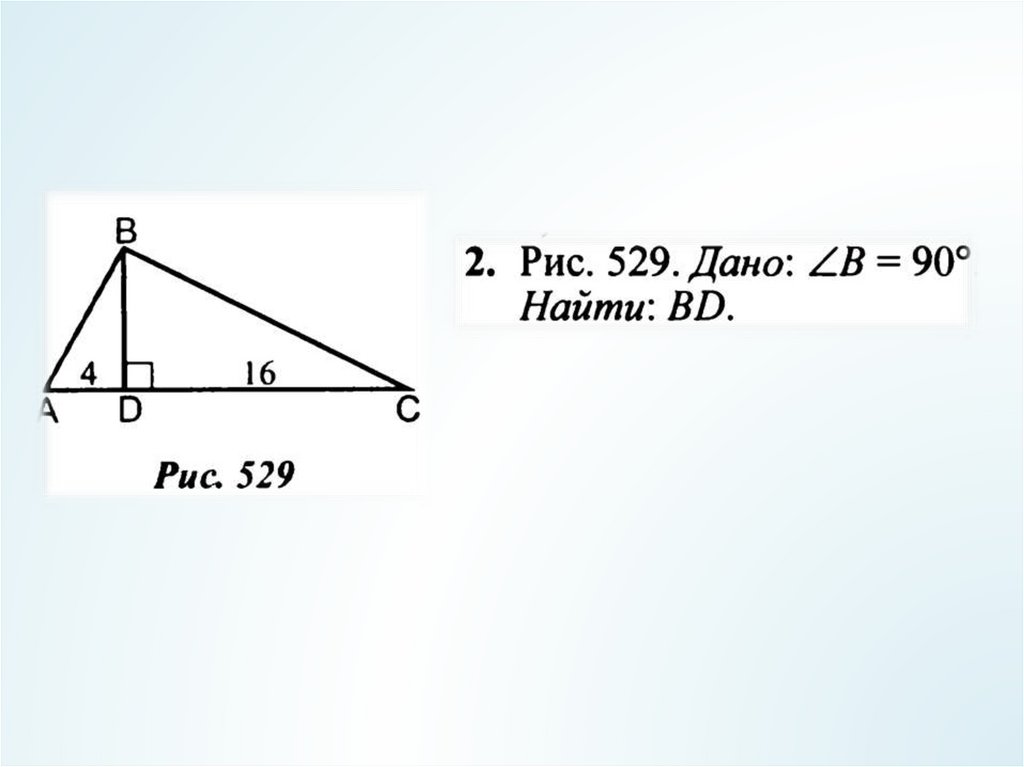
11. В классе

№ 572 (б, г)
№ 573

12. Домашнее задание

п 63 № 572(а, в, д), 575