Пропорциональные отрезки в прямоугольном треугольнике

1.

«Пропорциональные отрезки
в прямоугольном
треугольнике»

2.

Ученик, который учится без желания,
подобен птице без крыльев.
Саади
персидский мыслитель и писатель, 13 в.н.э.

3.

Задание :
в прямоугольном треугольнике
отыскать пропорциональные отрезки
и раскрыть некоторые его важные свойства

4.

Верно ли утверждение:
два любых прямоугольных
треугольника – подобны
?

5.

Свойство прямоугольного треугольника.
Высота прямоугольного
треугольника, проведенная из
вершины прямого угла,
разделяет
треугольник на два подобных
треугольника, каждый из
которых подобен данному.

6.

Свойство прямоугольного треугольника
С
Дано: АВС,
СН АВ
Доказать:
А
Н
В
АСВ = 900,
АСН и
АСН и
СВН и
СВН подобны
АВС подобны
АВС подобны
Доказательство:
Пусть
А = , тогда
АСН = 900 - ,
В= 900 - ,
ВСН = 900 - ( 900 - ) = .
Итак, прямоугольные треугольники АСН и СВН подобны, т.к.
А=
прямоугольные треугольники АСН и АВС подобны, т.к.
А - общий,
прямоугольные треугольники СВН и АВС подобны, т.к.
В – общий.
ВСН,

7.

Определение.
Отрезок XY называется средним геометрическим
(или средним пропорциональным) между отрезками
АВ и CD, если
XY AB CD
а).Найдите среднее пропорциональное
отрезков MN и KP, если MN=4, KP=25
XY
MN KP
4 25 10

8.

б). Найдите длину отрезка AB, если среднее
пропорциональное отрезков AB и СD равно 90см и
CD=100 см
XY AB CD
XY 2 AB CD
XY 2 90 90
AB
81
CD
100

9.

Утверждение1. Высота прямоугольного
треугольника, проведенная из вершины
прямого угла, есть среднее пропорциональное
между отрезками, на которые делится
гипотенуза этой высотой.
C
A
СD АD DB
D
B

10.

Свойство 1.
С
Дано: АВС,
СН АВ
АСВ = 900,
Доказать: СН =
А
Н
AH HB
В
Доказательство:
По доказанному АСН и СВН подобны, значит,
сходственные стороны пропорциональны:
АН
CH
CH
HB
, следовательно, СН2 = АН · НВ, т. е. СН =
AH HB

11.

1.
Реши задачу
?
5
2
·

12.

2.
Реши задачу
9
?
4

13.

Реши задачу
3.
8
1
?

14.

Реши задачу
4.
3
4
?

15.

Утверждение 2
Катет прямоугольного треугольника есть среднее
пропорциональное между гипотенузой и отрезком
гипотенузы, заключенным между этим катетом и
высотой, проведенной из вершины прямого угла.
C
AC АB AD
СB АB DB
A
D
B

16.

Свойство 2.
С
Дано:
АВС,
СН АВ
Доказать: АС =
А
Н
В
ВС =
АСВ = 900,
AB AH
AB BH
Доказательство:
По доказанному АСН и АВС подобны, значит,
сходственные стороны пропорциональны:
Значит,
АС2
= АВ · АН, т. е. АС =
AB AH
По доказанному ВСН и АВС подобны, значит,
сходственные стороны пропорциональны:
Значит, ВС2 = АВ · ВН, т. е. ВС =
AB BH
АВ
АС
АС
АН
АВ
ВС
ВС
ВН

17.

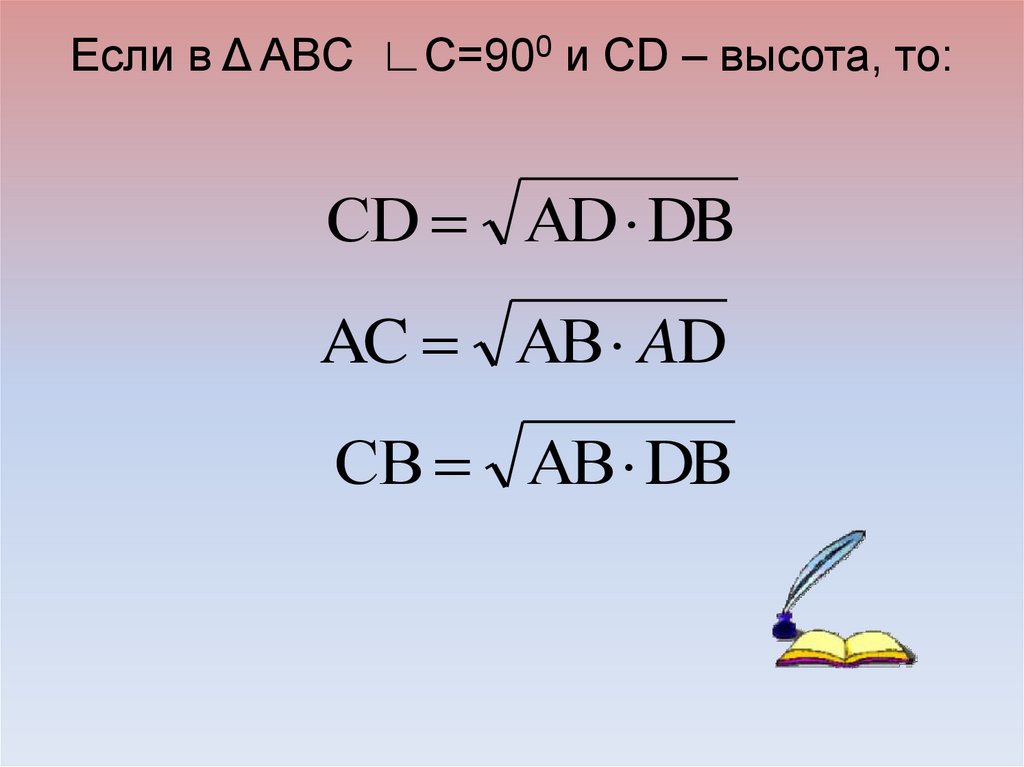
Если в Δ ABC ∟С=900 и CD – высота, то:
СD АD DB
AC АB AD
СB АB DB

18.

Задача 1.
Найдите неизвестные линейные элементы
прямоугольного треугольника АВС.
C
2 10
АС 18 20
6
ВС 2 20
B
6 10
2
D
18
А
DС 18 2

19.

Задача 2. Найдите неизвестные линейные элементы
прямоугольного треугольника АВС.
C
АС 16 25
ВС 9 25
20
12
А
16
D
DС 16 9
15
9
B

20.

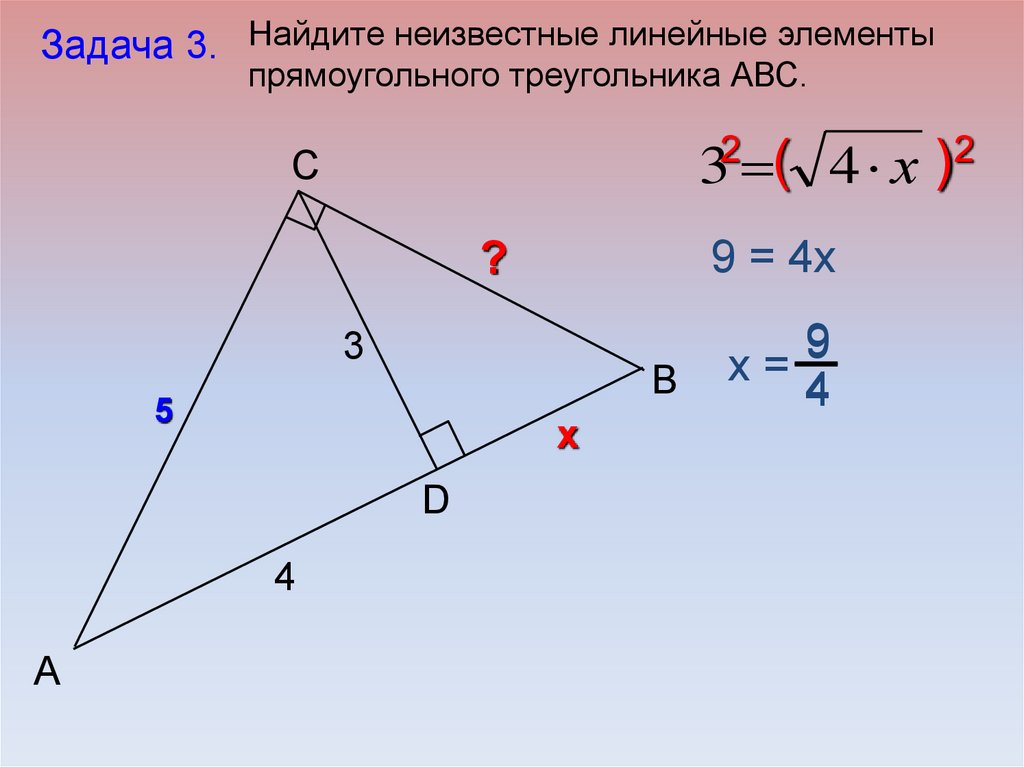
Задача 3. Найдите неизвестные линейные элементы
прямоугольного треугольника АВС.
2
(
)
3 4 х
2
C
9 = 4х
?
3
B
5
х
D
4
А
9
х=
4

21.

Вопрос 4:
Назовите пропорциональные отрезки
в прямоугольном треугольнике
Проверьте ответ:
Высота прямоугольного
треугольника, проведенная
из вершины прямого угла,
есть среднее пропорциональное
между проекциями катетов
на гипотенузу.
h2 = ac ∙ bc

22.

Вопрос 5:
Назовите пропорциональные отрезки
в прямоугольном треугольнике
Проверьте ответ:
Катет прямоугольного треугольника
есть среднее пропорциональное
между гипотенузой и проекцией
этого катета на гипотенузу.
а2 = c ∙ aс
b2 = c ∙ b с

23.

Решите задачи 1-2:
Найти пропорциональные отрезки
в прямоугольном треугольнике по формулам:
h2 = ac ∙ bc
а 2 = c ∙ aс
b 2 = c ∙ bс

24.

Задача1:
Найдите высоту в прямоугольном треугольнике
aс = 4
bс = 9
h=?
Решение:
h2 = ac ∙ b c
h2 = 4 ∙ 9
h=6
Ответ: h = 6

25.

Задача2:
Найдите катет прямоугольного треугольника
ac = 2
c=8
а=?
Решение:
a2 = c ∙ ac
a2 = 8∙2
a=4
Ответ: a
=4

26.

Решение задачи
В трапеции АВСК АВ АК, АС СК, ВС = 6, АК = 8.
Найдите углы трапеции.
В
А
6
С
К
Н
Решение:
Проведём СН АК,
т. к. АВСК – трапеция и АВ АК, то
АВСН – прямоугольник, АН = ВС = 6,
НК = АК – АН = 8 – 6 = 2.
Т. к. АС
СК, то
АСК – прямоугольный,
8
СН – высота, проведённая из вершины прямого угла, значит,
СН =
AH HK 6 2 12 2 3
По теореме Пифагора (
СНК) СК2 = СН2 + НК2, СК2 = 12 + 4 = 16, СК = 4.
(2 способ нахождения СК из
АСК: СК =
AK HK 8 2 16 4 )
В прямоугольном треугольнике СНК НК = ½ СК, значит, КСН = 300,
К = 900 – 300 = 600.
В трапеции АВСК
А = В = 900, К = 600, ВСК = 1800 – 600 = 1200.
Ответ: 900; 900; 1200; 600.